Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
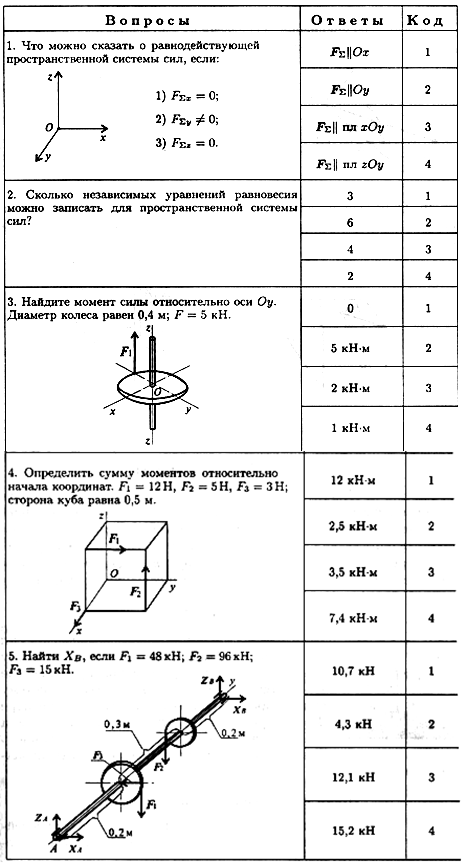
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1.5. Статика. Пространственная система силСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЛЕКЦИЯ 8 Тема 1.6. Центр тяжести Иметь представление о системе параллельных сил и центре системы параллельных сил, о силе тяжести и центре тяжести. Знать методы для определения центра тяжести тела и формулы для определения положения центра тяжести плоских фигур. Уметь определять положение центра тяжести простых геометрических фигур, составленных из стандартных профилей. Теорема Вариньона
Мгл = ΣFkl, где ΣFk - сумма перенесённых сил; l – расстояние от линии действия сил до точки приведения (плечи сил). Непосредственно из этого равенства вытекает важная зависимость между моментом равнодействующей и моментами составляющих сил, известная в механике как теорема Вариньона. Перепишем равенство в таком виде:
Мгл = ΣМ0(Fk) Поэтому последнее равенство можно переписать в виде
т. е. момент равнодействующей произвольной плоской системы сил относительно любой точки равен алгебраической сумме моментов сил системы, взятых относительно той же точки. С помощью теоремы Вариньона решаются многие задачи механики. В частности, легко определяется равнодействующая системы параллельных сил. Как это делается, покажем на примере.
Решение 1. Находим модуль равнодействующей. Как известно,
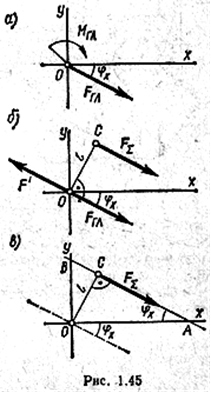
Но если ось х расположить перпендикулярно силам, а ось у — параллельно (рис. 1.47, а), направив ее положительный отсчет вниз, то проекции каждой из сил на ось х равны нулю и, значит,
а проекции сил на ось у равны их модулям с соответствующими знаками: F1y = F1 = 6 Н; F2y= F2 = 8 H; F3y = F3 = 10 H; F4y = F4 = 15 Н и F5y = F5 = 3H. Таким образом, модуль равнодействующей системы параллельных сил
Вектор равнодействующей FΣ направлен параллельно составляющим силам в сторону положительного отсчета оси у, если XFky > 0, и в сторону отрицательного отсчета, если ΣFky < 0.
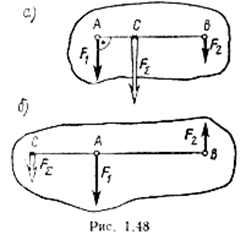
В данном случае FΣ = ΣFк = 6 — 8 + 10 + 15 — 3 = 20 Н, т. е. равнодействующая равна 20 Н и направлена вниз. 2. Изобразим эту равнодействующую условно штриховой линией на некотором расстоянии х от начала координат (рис. а) и запишем моменты всех сил относительно точки Ах'
И, согласно теореме Вариньона, получим — FΣx = F2 * A1A2 – F3 * A1A3 – F4 * A1A4 + F5 * A1A5 Отсюда после подстановки известных числовых значений сил и плеч —20 x = 8 – 0,2 — 10 – 0,4 — 15 – 0,6 + 3 – 0,8, получим
Следовательно, FΣ = 20 Н, а ее линия действия, параллельная составляющим силам, проходит от точки A1 на расстоянии l = 0,45 м (рис. 1.47,6).
Даны приложенные к телу параллельные силы F1 и F2, направленные в одну сторону. Согласно равенству FΣ = ΣFk ясно, что в данном случае
а вектор равнодействующей FΣ, приложенный в некоторой точке С, направлен параллельно силам в ту же сторону. Возьмем сумму моментов сил относительно точки С (точки, через которую проходит линия действия равнодействующей). Тогда
и, следовательно,
или
отсюда получаем известную из физики пропорциональную зависимость:
т. е. расстояния от линии действия двух параллельных сил до линии действия равнодействующей обратно пропорциональны силам.
Легко доказать (проделайте это самостоятельно), что такую же зависимость получим и при определении равнодействующей двух параллельных сил, направленных в противоположные стороны, хотя в этом случае модуль равнодействующей FΣ = F1 — F2. Направлена она в сторону большей по модулю силы, и линия ее действия расположена не между слагаемыми силами, а за большей из них (рис. б). Центр параллельных сил
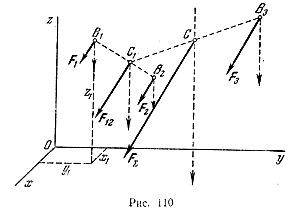
Пусть, например, к телу приложены в точках B1, В2 и В3 три параллельные и направленные в одну сторону силы F1, F2 и F3 (рис. 110). Сложив сначала по соответствующему правилу две силы F1 и F2, найдем их равнодействующую F12. Складывая затем по тому же правилу силу F12 с силой F3, найдем равнодействующую FΣ всех трех данных сил. Эта равнодействующая, очевидно, параллельна данным силам и направлена в ту же сторону. Модуль равнодействующей равен сумме модулей составляющих сил;
Остается определить положение точки С, через которую проходит линия действия равнодействующей. За точку приложения равнодействующей, конечно, может быть взята любая точка, лежащая на линии ее действия, но оказывается, что только одна из них, именно точка С, определенная путем последовательного сложения сил, обладает особым, весьма важным свойством. Свойство это состоит в том, что если мы повернем все данные силы вокруг их точек приложения на одинаковый угол, не нарушая их параллельности, то линия действия их равнодействующей, повернувшись на тот же самый угол (как показано на рис. 110 штриховыми линиями), будет вновь проходить через точку С. Точка С носит название центра системы параллельных сил.
Из сказанного выше следует, что центром данной системы параллельных сил называется точка, через которую проходит линия действия их равнодействующей при любом повороте сил системы вокруг их точек приложения на один и тот же угол в одну и ту же сторону. Выведем теперь формулы для определения координат центра системы параллельных сил. Возьмем пространственную систему осей координат и обозначим координаты точек приложения данных сил: В1 — соответственно x1, y, z1; В2 — x2, y2 z2; B3 – х3, у3, z3. Координаты центра параллельных сил С обозначим хС, уС , zС. Как известно, равнодействующей называется сила, эквивалентная данной системе сил, т. е. равнодействующая приложенная в точке С, производит на тело такое же действие, как и вся система сил F1, F2,.., Fk,..., Fn. Значит, согласно теореме Вариньона, момент равнодействующей относительно любой оси равен алгебраической сумме моментов сил относительно той же оси. Определим моменты сил относительно оси у.
Так как
где k принимает последовательно значения от 1 до п. Отсюда
где
Определив последовательно момент равнодействующей и моменты всех составляющих сил относительно оси х, найдем, что FΣyc= ΣFhyk, откуда следует формула для определения ординаты центра параллельных сил
Аналогичную формулу для третьей координаты (аппликаты) центра параллельных сил
получим, если повернем все силы на 90°, например так, чтобы они расположились параллельно оси у, и определим моменты сил относительно оси х. Следовательно, формулы координат центра параллельных сил имеют вид
где Fh — модули параллельных сил, xh, yk, zh — координаты точек их приложения. Сила тяжести
Сила тяжести — равнодействующая сил притяжения к Земле, распределенных по всему объему тела. Силы притяжения, приложенные к частицам твердого тела, образуют систему сил, линии действия которых сходятся в центре Земли (рис. 8.1). Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 3070; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 Пари параллельном переносе сил в точку главный момент системы
Пари параллельном переносе сил в точку главный момент системы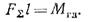
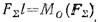 — момент равнодействующей относительно любой точки. Но
— момент равнодействующей относительно любой точки. Но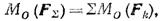
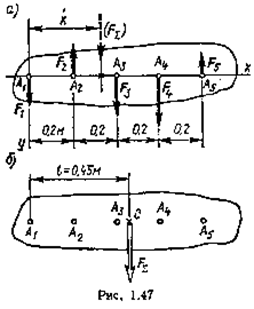 Пример. Определить равнодействующую пяти параллельных сил F1 = 6 Н, F2 = 8 Н, F3 = 10 Н, F4 = 15 Н, F5 = 3 Н, приложенных к телу, как показано на рисунке а.
Пример. Определить равнодействующую пяти параллельных сил F1 = 6 Н, F2 = 8 Н, F3 = 10 Н, F4 = 15 Н, F5 = 3 Н, приложенных к телу, как показано на рисунке а.
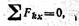
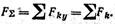
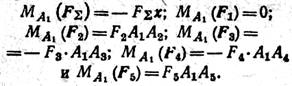
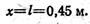
 Известные из физики зависимости, возникающие при сложении двух параллельных сил, можно получить из теоремы Вариньона.
Известные из физики зависимости, возникающие при сложении двух параллельных сил, можно получить из теоремы Вариньона.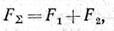

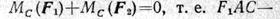
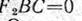
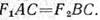
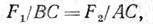
 Зная правила сложения двух параллельных сил, нетрудно путем последовательного сложения найти равнодействующую и для любой системы параллельных сил.
Зная правила сложения двух параллельных сил, нетрудно путем последовательного сложения найти равнодействующую и для любой системы параллельных сил.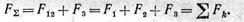
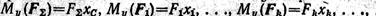
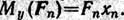
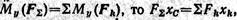
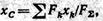
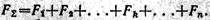 Поэтому формула для определения абсциссы центра параллельных сил принимает окончательный вид
Поэтому формула для определения абсциссы центра параллельных сил принимает окончательный вид