
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. 2. Статика. Проекции силы на осьСодержание книги
Поиск на нашем сайте
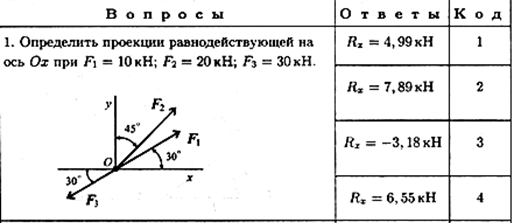
Практическое занятие №1. Плоская система сходящихся сил Знать способы сложения двух сил и разложение силы на составляющие, геометрический и аналитический способы определения равнодействующей силы, условия равновесия плоской сходящейся системы сил. Уметь определять равнодействующую системы сил, решать задачи на равновесие геометрическим и аналитическим способом, рационально выбирая координатные оси. Расчетные формулы Равнодействующая системы сил
где F∑x, F∑ y — проекции равнодействующей на оси координат; Fkx, Fky — проекции векторов-сил системы на оси координат.
где — угол равнодействующей с осью Ох. Условие равновесия
Если плоская система сходящихся сил находится в равновесии, многоугольник сил должен быть замкнут.
Пример 1. Определение равнодействующей системы сил.
Определить равнодействующую плоской системы сходящихся сил аналитическим и геометрическим способами (рис. П1.1). Дано:
Решение 1. Определить равнодействующую аналитическим способом (рис. П1.1a).
2. Определить равнодействующую графическим способом.
С помощью транспортира в масштабе 2 мм = 1 кН строим многоугольник сил (рис. П1.1б). Измерением определяем модуль равнодействующей силы и угол наклона ее к оси Ох.
Результаты расчетов не должны отличаться более чем на 5%:
Расчетно-графическая работа №1. Определение равнодействующей плоской системы сходящихся сил аналитическим и геометрическим способами
Задание 1. Используя схему рис. П1.1а, определить равнодействующую системы сил геометрическим способом
Пример 2. Решение задачи на равновесие аналитическим способом.
Грузы подвешены на стержнях и канатах и находятся в равновесии. Определить реакции стержней АВ и СВ (рис. П1.2). Решение
1. Определяем вероятные направления реакций (рис. П1.2а). Мысленно убираем стержень АВ, при этом стержень СВ опускается, следовательно, точка В отодвигается от стены: назначение стержня АВ — тянуть точку В к стене. Если убрать стержень СВ, точка В опустится, следовательно, стержень СВ поддерживает точку В снизу — реакция направлена вверх. 2. Освобождаем точку В от связи (рис. П1.26). 3. Выберем направление осей координат, ось Ох совпадает с реакцией R1. 4. Запишем уравнения равновесия точки В:
5. Из второго уравнения получаем:
Из первого уравнения получаем:
Вывод: стержень АВ растянут силой 28,07 кН, стержень СВ сжат силой 27,87 кН.
Примечание. Если при решении реакция связи окажется отрицательной, значит, вектор силы направлен в противоположную сторону. В данном случае реакции направлены верно.
Задание 2. Определить реакции стержней АС и AD (рис. П1.3) в аналитической форме.
При защите работ ответить на вопросы карт с тестовыми заданиями. Темы 1.1, 1.2. Статика. Плоская сходящаяся система сил
Задание для самостоятельной работы 1.
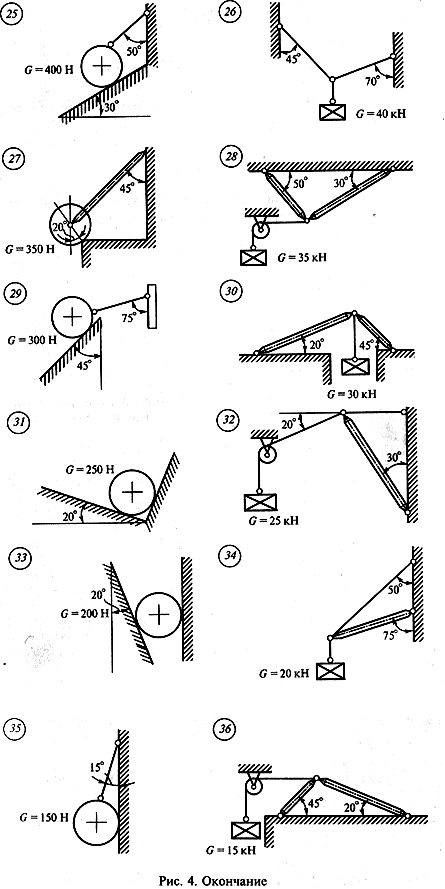
Определить величину и направление реакций связей по данным одного из вариантов, показанных на рисунке. Задача 1
Задача 2. Определить реакции стержней, удерживающих грузы F1 и F2. Массой стержней пренебречь. Схему своего варианта см. на рисунке. Числовые данные своего варианта взять из таблицы.
ЛЕКЦИЯ 4 Тема 1.3. Пара сил и момент силы относительно точки
Уметь определять моменты пар сил и момент силы относительно точки, определять момент результирующей пары сил. Пара сил, момент пары сил
Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны.
Рассмотрим систему сил (F, F 1), образующих пару.
Свойства пар (без доказательств):
Момент равнодействующей пары равен алгебраической сумме моментов пар, составляющих систему (рис. 4.3):
4. Равновесие пар.
Для равновесия пар необходимо и достаточно, чтобы алгебраическая сумма моментов пар системы равнялась нулю:
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 8351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |


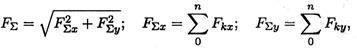


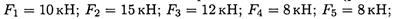







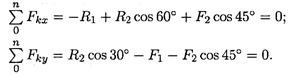
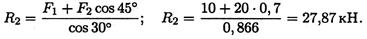






 Знать обозначение, модуль и определение моментов пары сил или относительно точки, условия равновесия системы пар сил.
Знать обозначение, модуль и определение моментов пары сил или относительно точки, условия равновесия системы пар сил.





