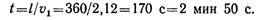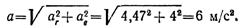Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мгновенным центром скоростей (МЦС) является точка на плоскости, абсолютная скорость которой в данный момент равна нулю.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
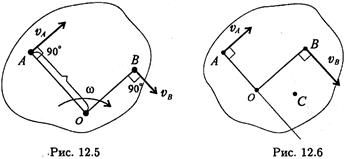
Вокруг этой точки тело совершает поворот со скоростью ω. Скорость точки А в данный момент равна vA = ωOA, т.к. vA — линейная скорость точки А, вращающейся вокруг МЦС. Существуют три способа определения положения мгновенного центра скоростей. Первый способ. Известна скорость одной точки тела vA и угловая скорость вращения тела ω (рис. 12.5). Точку О находим на перпендикуляре к вектору скорости vA: AO = vA/ω
Соединяем точку О с точкой B, замеряем расстояние ОВ.
vB ┴ ОВ, vB = ωОВ.
Второй способ. Известны скорости двух точек тела va и vb, и они не параллельны (рис. 12.6). Проводим из точек А и В два перпендикуляра к известным векторам скоростей. На пересечении перпендикуляров находим МЦС. Далее можно найти скорость любой точки С vC /vB = OC/OB Третий способ. Известны скорости двух точек тела, и они параллельны (va\\vb) (рис. 12.7).
Соединяем концы векторов, МЦС находится на пересечении линии, соединяющей концы векторов с линией АВ (рис. 12.7). При поступательном движении тела (рис. 12.7в) МЦС отсутствует. Примеры решения задач
Пример 1. Рассмотрим механизм, в котором стержень OA вращается вокруг точки О со скоростью ω. Вдоль стержня перемещается ползун М со скоростью vM (рис. 12.8). Определить абсолютную скорость точки М. Решение 1. Относительное движение — вдоль стержня; скорость vr = vM 2. Переносное движение — вращение стержня; скорость ve = ωОМ. 3. Скорость абсолютного движения
Пример 2. Стержень А В соскальзывает вниз, опираясь концами о стену и пол (рис. 12.9). Длина стержня 1,5 м; в момент, изображенный на чертеже, скорость точки В vb — 3 м/с. Найти скорость точки А. Решение
По известной скорости vb определяем угловую скорость ш стержня:
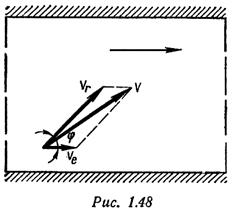
Сложное движение точки Пример 3. Лодочник, переправляясь через реку, направил лодку под углом φ = 45° к направлению течения (рис. 1.48). В стоячей воде лодка движется со скоростью 3 м/с. Скорость течения реки 1 м/с. Определить абсолютную скорость движения лодки, а также время, в течение которого лодка переплывет реку шириной l = 360 м.
Относительно берега лодка совершает сложное движение: относительно потока воды и одновременно с потоком воды. Движение лодки относительно потока (как бы в стоячей воде) — относительное, движение ее вместе с потоком — переносное. Тогда vr = 3 м/с, ve =1 м/с. Как известно,
Графическое определение абсолютной скорости лодки представлено на рис. 1.48. Модуль абсолютной скорости вычисляется по формуле
Подставляя числовые значения, получаем:
Чтобы определить время, за которое лодка пересечет реку, необходимо найти составляющую скорости vl поперек течения реки:
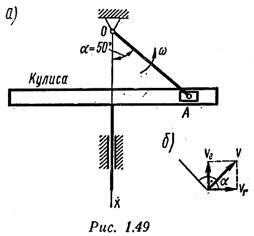
Пример 4. В кривошипно-кулисном механизме с поступательно движущейся по вертикали кулисой частота вращения кривошипа OA п = 90 об/мин (рис. 1.49, а). Длина кривошипа СМ = 0,3 м. Конец кривошипа соединен шарнирно с ползуном А, скользящим по горизонтальному пазу кулисы. Определить скорость кулисы в тот момент, когда кривошип образует с вертикальной осью движения кулисы угол α = 50°. Решение
Движение точки А вместе с кривошипом считаем сложным; оно получается в результате сложения: а) движения точки А вместе с кулисой в ее возвратно-поступательном движении вдоль оси х (переносном движении); б) движения точки А вместе с кулисным камнем, движущимся возвратно-поступательно в прорези кулисы в направлении, перпендикулярном оси х (относительном движении). На рис. 1.49, б представлено графическое решение задачи.
Как видно из рис 1.49, б,
Пример 5. Автомобиль движется по прямолинейному пути с ускорением а = 4 м/с2. На продольном валу насажен вращающийся маховичок радиусом г = 0,25 м (рис. 1.50, а), имеющий в данный момент угловую скорость ω = 4 рад/с и угловое ускорение ε = 8 рад/с2. Найти абсолютное ускорение точек обода маховичка в данный момент (рис. 1.50, б). Решение
Относительно поверхности земли точки обода маховичка совершают сложное движение. За переносное движение принимаем движение автомобиля, за относительное — вращательное движение маховичка относительно неподвижной оси
Очевидно, что
В относительном движении точка движется по окружности г = 0,25 м и ее ускорение вычисляется по формуле
На рис. 1.50, б показаны составляющие ускорения точки обода маховичка в относительном движении, а также вектор а, Так как а, и ае взаимно перпендикулярны, то
Вектор а показан на рис. 1.50, б.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1663; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.183.34 (0.008 с.) |


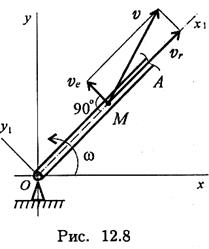

 Найдем положение МЦС. Скорости точек А и В направлены вдоль стены и вдоль пола. Восстанавливая перпендикуляры к векторам скоростей, находим МЦС.
Найдем положение МЦС. Скорости точек А и В направлены вдоль стены и вдоль пола. Восстанавливая перпендикуляры к векторам скоростей, находим МЦС.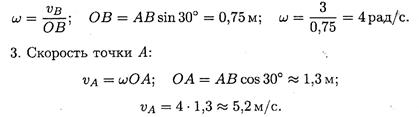
 Решение
Решение


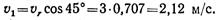
 Время движения лодки
Время движения лодки