
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мгновенная и средняя скоростьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр. Когда говорят о средней скорости, для различения, скорость согласно выше приведённому определению называют мгновенной скоростью. Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля. 2.1. Кинематика частицы Если размеры тела при описании его движения несущественны, то его движение можно рассматривать как движение частицы в пространстве. Это самая простая модель для описания реального тела. Так как в дальнейшем будут рассматриваться движения тела обладающего массой, но в пренебрежении ее размерами, внутренней структуры и формы, то введем в рассмотрение единый термин частица, понимая под ним материальную точку. Существует три способа описания движения частицы: векторный (геометрический), координатный и естественный. Рассмотрим их последовательно, учитывая, то аналогичное построение описания движения частицы будет применимо в релятивистском случае. Векторный способ. В этом способе положение интересующей нас частицы А задают радиусом-вектором
Геометрическое место точек, где тело побывало за время своего движения, называется траекторией частицы А. При векторном способе описания траекторией будет положение концов радиус-вектора Введем понятие скорости частицы. Скорость характеризует быстроту движения частицы. Пусть за промежуток времени
Это значит, что вектор скорости
Заметим, что в общем случае модуль приращения радиус-вектора Движение частицы характеризуется также ускорением. Вектор ускорения
т. е. равен производной от вектора скорости по времени. Направление вектора
где Модуль вектора скорости
Таким образом, зная зависимость Возникает и обратная задача: можно ли найти Оказывается, для получения однозначного решения этой задачи одной зависимости Определим сначала скорость частицы
Но величина
Аналогично вычисляется и радиус-вектор
Для нахождения самого радиус-вектора или
Рассмотрим в качестве примера движение камня, брошенного под некоторым углом к горизонту с начальной скоростью
т. е. в этом случае
Для полного решения задачи о движении частицы - определения скорости Координатный способ. В этом способе с телом отсчета жестко связывают определенную систему координат (декартову, косоугольную или криволинейную). Выбор вида системы координат определяется рядом соображений: характером или симметрией задачи, постановкой вопроса, а также стремлением упростить математическое решение задачи. Для простоты рассмотрим декартову систему координат x,у,z. Изучение движений частицы в других координатах оставим для задач. Запишем проекции радиус-вектора
Закон движения частицы - это зависимость координат от времени. Он задает положение частицы в каждый момент времени, ее скорость и ускорение. Cпроектировав (2.1) и (2.2), например, на OX, получим формулы, определяющие проекции векторов скорости и ускорения на эту ось:
где dx- проекция вектора перемещения
здесь Зависимости
а направление вектора
где (, (,(- углы между вектором С помощью закона движения можно найти траекторию частицы, зависимость пройденного ею пути от времени, зависимость скорости от положения частицы и т.д. Нахождение скорости и закона движения частицы по заданному ускорению называется обратной задачей. Ее решение проводится, как и в векторном способе, путем интегрирования (в данном случае проекций ускорения по времени). Задача и здесь имеет однозначное решение, если кроме ускорения заданы еще и начальные условия: проекции скорости и координаты частицы в начальный момент времени. Естественный способ. Его применяют в том случае, когда заранее известна траектория частицы. Положение движущегося тела определяют дуговой координатой l - расстоянием вдоль траектории от выбранного начала отсчета точки О (рис. 2.3).
При этом произвольно выбирают положительное направление отсчета координаты l (например, как показано стрелкой на рисунке 2.3). Движение частицы задано полностью, если определена ее траектория, начало отсчета О, положительное направление отсчета дуговой координаты l и закон движения частицы, т. е. зависимость Рассмотрим как в этом способе описания определяется скорость частицы. Введем единичный вектор
где
Рассмотрим теперь ускорение частицы
Преобразуем последнее слагаемое этого выражения:
Рассмотрим приращение вектор
Можно строго показать, что при стремлении точки 2 к точке 1 отрезок траектории между ними можно представить в виде дуги окружности с центром в некоторой точке О. Ее называют центром кривизны траектории в данной точке, а радиус R соответствующей окружности - радиусом кривизны траектории в той же точке. Как видно из рис. 2.4, угол
Подставляя (2.8) в (2.7), а затем полученное выражение - в (2.6), получим в итоге выражение для вектора ускорения
Здесь первое слагаемое называют тангенциальным ускорением
В итоге полное ускорение Модуль полного ускорения вычисляется по теореме Пифагора
Точка А движется по дуге окружности радиусом R (рис. 2.5).
Ее скорость зависит от дуговой координаты l но закону Из рис. 2.5 видно, что угол (можно определить из соотношения составляющих полного ускорения по формуле
Отсюда получаем
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.012 с.) |

 , проведенным из некоторой неподвижной точки О выбранной системы отсчета в точку А. Под системой отсчета в механике понимают совокупность: тело отсчета, способ измерения расстояний ("линейка") и способ измерения времени ("часы"). При движении частицы А ее радиус-вектор меняется в общем случае как по модулю, так и по направлению, т. е. радиус-вектор
, проведенным из некоторой неподвижной точки О выбранной системы отсчета в точку А. Под системой отсчета в механике понимают совокупность: тело отсчета, способ измерения расстояний ("линейка") и способ измерения времени ("часы"). При движении частицы А ее радиус-вектор меняется в общем случае как по модулю, так и по направлению, т. е. радиус-вектор  зависит от времени t.
зависит от времени t.
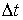 точка А переместилась из точки 1 в точку 2 (рис. 2.1). Из рисунка видно, что вектор перемещения
точка А переместилась из точки 1 в точку 2 (рис. 2.1). Из рисунка видно, что вектор перемещения  частицы А представляет собой приращение радиус-вектора
частицы А представляет собой приращение радиус-вектора  . Отношение
. Отношение  называют средним вектором скорости <
называют средним вектором скорости <  > за время (t. Вектор <
> за время (t. Вектор < 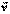 > совпадает по направлению с
> совпадает по направлению с  . Определим теперь вектор скорости
. Определим теперь вектор скорости  при (t® 0, т. е.
при (t® 0, т. е.
 частицы в данный момент времени равен производной от радиус-вектора
частицы в данный момент времени равен производной от радиус-вектора  ). Модуль вектора
). Модуль вектора 
 . Например, если
. Например, если  но
но  .
. определяет скорость изменения вектора скорости
определяет скорость изменения вектора скорости  со временем:
со временем:
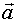 совпадает с направлением вектора
совпадает с направлением вектора  - приращением вектора
- приращением вектора  ,
, и
и  - постоянные векторы. Найдем скорость
- постоянные векторы. Найдем скорость 
 .
. , можно найти скорость
, можно найти скорость  частицы в каждый момент времени.
частицы в каждый момент времени. и
и  , зная зависимость от времени ускорения
, зная зависимость от времени ускорения  ?
?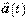 недостаточно, так как необходимо еще знать начальные условия, а именно - скорость
недостаточно, так как необходимо еще знать начальные условия, а именно - скорость  и радиус-вектор
и радиус-вектор  частицы в некоторый начальный момент
частицы в некоторый начальный момент  . Чтобы в этом убедиться, рассмотрим простой случай, когда при движении ускорение частицы
. Чтобы в этом убедиться, рассмотрим простой случай, когда при движении ускорение частицы  . Согласно (2.2), за интервал времени dt малое приращение скорости
. Согласно (2.2), за интервал времени dt малое приращение скорости  . Интегрируя это выражение по времени от t = 0 до t, определим конечное приращение вектора скорости за это время:
. Интегрируя это выражение по времени от t = 0 до t, определим конечное приращение вектора скорости за это время: .
. - это еще не искомая скорость
- это еще не искомая скорость  в начальный момент времени
в начальный момент времени  . Тогда
. Тогда  , или
, или
 частицы. Согласно (2.1), за интервал времени dt малое приращение радиус-вектора
частицы. Согласно (2.1), за интервал времени dt малое приращение радиус-вектора 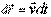 . После интегрирования этого выражения с учетом определенной выше зависимости
. После интегрирования этого выражения с учетом определенной выше зависимости  , определим приращение радиуса-вектора за время от t = 0 до t:
, определим приращение радиуса-вектора за время от t = 0 до t: .
. необходимо знать положение частицы в начальный момент времени
необходимо знать положение частицы в начальный момент времени  . Тогда
. Тогда  ,
,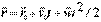 .
. . Если считать, что камень движется с постоянным ускорением
. Если считать, что камень движется с постоянным ускорением  , то его положение относительно начальной точки движения (
, то его положение относительно начальной точки движения ( ) определяется радиус-вектором
) определяется радиус-вектором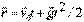 .
.
 и положение
и положение  частицы в начальный момент времени.
частицы в начальный момент времени. на оси координат. Вектор
на оси координат. Вектор 
 ,
,
 на ось х,
на ось х,
 - проекция вектора приращения скорости
- проекция вектора приращения скорости  полностью определяют движение частицы. Зная их, можно найти не только положение частицы, но и проекции ее скорости и ускорения, а следовательно, модуль и направление векторов
полностью определяют движение частицы. Зная их, можно найти не только положение частицы, но и проекции ее скорости и ускорения, а следовательно, модуль и направление векторов  ,
, задается направляющими косинyсами по формулам:
задается направляющими косинyсами по формулам:
 . Аналогичными формулами определяются модуль и направление вектора ускорения
. Аналогичными формулами определяются модуль и направление вектора ускорения 
 .
. , связанный с движущейся точкой А и направленный по касательной к траектории в сторону увеличения дуговой координаты l (рис. 2.3). Ясно, что
, связанный с движущейся точкой А и направленный по касательной к траектории в сторону увеличения дуговой координаты l (рис. 2.3). Ясно, что 
 - проекция вектора
- проекция вектора  на направление вектора
на направление вектора  - величина алгебраическая. Кроме того, ясно, что
- величина алгебраическая. Кроме того, ясно, что


 на участке dl (рис. 2.4).
на участке dl (рис. 2.4).
 , откуда
, откуда  , причем при
, причем при 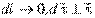 . Если ввести единичный вектор нормали
. Если ввести единичный вектор нормали  к траектории в точке 1, направленный к центру кривизны, то последнее равенство запишется в векторном виде:
к траектории в точке 1, направленный к центру кривизны, то последнее равенство запишется в векторном виде:

 , а второе - нормальным (центростремительным)
, а второе - нормальным (центростремительным) 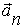

 может быть представлено как сумма тангенциального
может быть представлено как сумма тангенциального  и нормального
и нормального  ускорений.
ускорений.

 где
где  постоянная (определите эту константу самостоятельно). Найдем угол (между векторами полного ускорения и скорости частицы как функцию координаты l.
постоянная (определите эту константу самостоятельно). Найдем угол (между векторами полного ускорения и скорости частицы как функцию координаты l. . Значения компонент вектора полного ускорения
. Значения компонент вектора полного ускорения  и
и  . Вычисляются по формулам:
. Вычисляются по формулам:
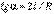 .
.


