
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вращение твердого тела вокруг неподвижной оси. Средние и мгновенные угловые скорость и ускорение.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Враще́ние — круговое движение объекта. В плоском пространстве объект вращается вокруг центра (или точки) вращения. В трёхмерном пространстве объект вращается вокруг линии, называемой осью. Если ось вращения расположена внутри тела, то говорят, что тело вращается само по себе или обладает спином, который имеет относительную скорость и может иметь момент импульса. Круговое движение относительно внешней точки, например, вращение Земли вокруг Солнца, называется орбитальным движением или, более точно, орбитальным вращением. При равномерном вращении (T оборотов в секунду), Частота вращения — число оборотов тела в единицу времени. Период вращения — время одного полного оборота. Период вращения T и его частота ν связаны соотношением T = 1 / ν. Линейная скорость точки, находящейся на расстоянии R от оси вращения Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: mi — масса i -й точки, ri — расстояние от i -й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как массатела является мерой его инертности в поступательном движении. Кинетическая энергия вращательного движения
где Iz — момент инерции тела относительно оси вращения. ω — угловая скорость Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходныхпаровых машин определяли, просто «вручную» подсчитывая число оборотов за единицу времени. Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью
где Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела. При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно[1]:
Вектор углового ускорения α направлен вдоль оси вращения (в сторону При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени[2], то есть
и направлен по касательной к годографу вектора Существует связь между тангенциальным и угловым ускорениями:
где R — радиус кривизны траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/сек2.
Первый закон Ньютона и инерциальная система отсчета. Первый закон Ньютона Первый закон механики, или закон инерции (инерция – это свойство тел сохранять свою скорость при отсутствии действияна негодругих тел), как его часто называют, был установлен еще Галилеем. Но строгую формулировку этого закона дал и включил его в число основных законов механики Ньютон. Закон инерции относится к самому простому случаю движения – движению тела,на которое не оказывают воздействия другие тела. Такие тела называются свободными телами. Ответить на вопрос, как движутся свободные тела, не обращаясь к опыту,нельзя. Однако нельзя поставить ни одного опыта, который бы в чистом виде показал, как движется ни с чем не взаимодействующее тело, так как таких тел нет. Как же быть? Имеется лишь один выход. Надо создать для тела условия, при которых влияние внешних воздействий можно делать все меньшим и меньшим, и наблюдать, к чемуэто ведет. Можно, например, наблюдать за движением гладкого камняна горизонтальной поверхности, после того как ему сообщена некоторая скорость. (Притяжение камня к земле уравновешивается действием поверхности,на которую он опирается, и на скорость его движения влияет только трение.) При этом легко обнаружить, что чем более гладкой является поверхность, тем медленнее будет уменьшаться скорость камня. На гладком льду камень скользит весьма долго, заметно не меняя скорость. Трение можно уменьшить до минимумас помощью воздушной подушки – струй воздуха, поддерживающих тело над твердой поверхностью, вдоль которой происходит движение. Этот принциписпользуется в водном транспорте (суда на воздушной подушке). На основеподобных наблюдений можно заключить: если бы поверхность была идеально гладкой, то при отсутствии сопротивления воздуха (в вакууме) камень совсемне менял бы своей скорости. Именно к такому выводу впервые пришел Галилей. С другой стороны, нетрудно заметить, что, когда скорость тела меняется, всегда обнаруживается воздействие на него других тел. Отсюда можно прийти к выводу,что тело, достаточно удаленноеот другихтел и по этой причинене взаимодействующеес ними,движетсяс постояннойскоростью. Движение относительно, поэтому имеет смысл говорить лишь о движении тела по отношению к системе отсчета, связанной с другим телом. Сразу же возникает вопрос: будет ли свободное тело двигаться с постоянной скоростью по отношению к любому другому телу? Ответ, конечно, отрицательный. Так, если по отношению к Земле свободное тело движется прямолинейно и равномерно, то по отношению к вращающейся карусели тело заведомо так двигаться не будет. Наблюдения за движениями тел и размышления о характере этих движений приводят нас к заключению о том, что свободные тела движутся с постояннойскоростью, по крайней мере, по отношению к определенным телам и связаннымс ними системам отсчета. Например, по отношению к Земле. В этом состоит главное содержание закона инерции. Поэтому первый закон Ньютона может быть сформулирован так: существуют такие системы отсчета, относительно которых тело (материальная точка) при отсутствии на неё внешних воздействий (или при их взаимнойкомпенсации) сохраняет состояние покоя или равномерного прямолинейного движения. Инерциальная система отсчета Первый закон Ньютона утверждает (которое с той или иной степенью точности можно проверить на опыте) о том, что инерциальные системы существуютв действительности. Этот закон механики ставит в особое, привилегированное положение инерциальные системы отсчета. Системы отсчета,в которыхвыполняется первый закон Ньютона, называют инерциальными. Или Инерциальные системы отсчета – это системы, относительно которых материальная точка при отсутствиина неевнешних воздействий илиих взаимнойкомпенсации покоится или движется равномернои прямолинейно. Инерциальных систем существует бесконечное множество. Система отсчета, связанная с поездом, идущим с постоянной скоростью по прямолинейному участку пути, – тоже инерциальная система (приближенно), как и система,связанная с Землей. Все инерциальные системы отсчета образуют класс систем, которые движутся друг относительно друга равномерно и прямолинейно.Ускорения какого-либо тела в разных инерциальных системах одинаковы. Как установить, что данная система отсчета является инерциальной? Это можносделать только опытным путем. Наблюдения показывают, что с очень высокой степенью точности можно считать инерциальной системой отсчета гелиоцентрическую систему, у которой начало координат связано с Солнцем,а оси направлены на определенные «неподвижные» звезды. Системы отсчета, жестко связанные с поверхностью Земли, строго говоря, не являютсяинерциальными, так как Земля движется по орбите вокруг Солнца и при этом вращается вокруг своей оси. Однако при описании движений, не имеющихглобального (т. е. всемирного) масштаба, системы отсчета, связанные с Землей,можно с достаточной точностью считать инерциальными. С гораздо большей точностью можно считать инерциальной систему отсчета,в которой начало координат совмещено с центром Солнца, а координатные оси направлены к неподвижным звездам. Эту систему отсчета называют гелиоцентрической. Инерциальными являютсяи системыотсчета, которые движутся равномернои прямолинейноотносительнокакой-либоинерциальной системы отсчета. Галилей установил, что никакими механическими опытами, поставленными внутри инерциальной системы отсчета, невозможно установить, покоится эта система или движется равномернои прямолинейно. Это утверждение носит название принципа относительности Галилея или механического принципа относительности. Этот принцип был впоследствии развит А. Эйнштейном и является однимиз постулатов специальной теории относительности. Инерциальные системы отсчета играют в физике исключительно важную роль, так как, согласно принципу относительности Эйнштейна, математическое выражение любою закона физики имеет одинаковый вид в каждой инерциальной системе отсчета.В дальнейшем мы будем пользоваться только инерциальными системами(не упоминая об этом каждый раз). Системы отсчета,в которыхпервый закон Ньютонане выполняется,называют неинерциальными. К таким системам относится любая система отсчета, движущаяся с ускорениемотносительно инерциальной системы отсчета. В механике Ньютона законы взаимодействия тел формулируются для класса инерциальных систем отсчета. Примером механического эксперимента, в котором проявляется неинерциальность системы, связанной с Землей, служит поведение маятника Фуко. Так называетсямассивный шар, подвешенный на достаточно длинной нити и совершающий малые колебания около положения равновесия. Если бы система, связанная с Землей,была инерциальной, плоскость качаний маятника Фуко оставалась бы неизменной относительно Земли. На самом деле плоскость качаний маятника вследствие вращения Земли поворачивается, и проекция траектории маятникана поверхность Земли имеет вид розетки (рис. 1).
Рис. 1. О том, что телу свойственно сохранять не любое движение, а именнопрямолинейное, свидетельствует, например, следующий опыт (рис. 2). Шарик, двигавшийся прямолинейно по плоской горизонтальной поверхности, сталкиваясьс преградой, имеющей криволинейную форму, под действием этой преграды вынужден двигаться по дуге. Однако когда шарик доходит до края преграды,он перестает двигаться криволинейно и вновь начинает двигаться по прямой. Обобщая результаты упомянутых (и аналогичных им) наблюдений, можно сделать вывод, что еслинаданноетелонедействуютдругиетелаилиихдействиявзаимнокомпенсируются, этотелопокоитсяилижескоростьегодвиженияостаетсянеизменнойотносительносистемыотсчета, неподвижносвязаннойсповерхностьюЗемли.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 927; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.011 с.) |

 ,
, ,
,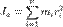 ,
,
 ,
, определяется формулой:
определяется формулой:
 — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) r от оси вращения можно считать так: v = r ω. Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.
— радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) r от оси вращения можно считать так: v = r ω. Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.
 при ускоренном вращении и противоположно
при ускоренном вращении и противоположно  ,
, ,
,




