
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первое начало термодинамики и его применение к изопроцессам. Теплоемкость идеального газа.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил Первое начало термодинамики: § при изобарном процессе
§ при изохорном процессе (A = 0)
§ при изотермическом процессе (Δ U = 0)
Здесь Молярная теплоемкость — теплоемкость 1 моля идеального газа.
Адиабатический В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть Изотермический В изотермическом процессе постоянна температура, то есть Изохорный В изохорическом процессе постоянен объем, то есть
А для идеального газа
Таким образом,
где i — число степеней свободы частиц газа. Изобарный В изобарном процессе (
CP=δQ/νΔT=CV+R=((i+2)/2)*R Вывод формулы для теплоемкости в данном процессе Согласно 1 началу термодинамики существует 2 способа изменить внутреннюю энергию тела (в нашем случае идеального газа): передать ему тепло или совершить над ним работу. dU=δQ+δA, где δA — работа окр. среды над газом. δAокр.среды=-δAгаза δQ=dU+δAгаза В расчете на 1 моль: С=δQ/ΔT=(ΔU+pΔV)/ΔT ΔU=CV*ΔT C=CV+(pΔV/ΔT)в данном процессе
Адиабатный и политропные процессы. Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии. Серьёзное исследование адиабатических процессов началось с XVIII века[1]. Адиабатический процесс является частным случаем политропного процесса. Адиабатические процессы обратимы, если их проводить достаточно медленно (квазистатически). В общем случае адиабатический процесс необратим. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы[2].
Если термодинамический процесс в общем случае являет собой три процесса - теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии[4], то адиабатический процесс в силу отсутствия теплообмена (Δ Q = 0) системы со средой сводится только к последним двум процессам[5]. Поэтому, первое начало термодинамики в этом случае приобретает вид
Энтропия (S) системы в обратимом адиабатическом процессе не меняется:
Благодаря этому адиабатический процесс может быть составной частью обратимого цикла. Вывод уравнения Согласно закону Менделеева — Клапейрона[5]:
Продифференцировав обе части, получаем:
Если в (3) подставить dT из (2), а затем dU из (1), получим:
или, введя коэффициент
Или
что после интегрирования даёт:
Окончательно имеем,
что и требовалось доказать. При адиабатическом процессе показатель адиабаты равен Политропный процесс — термодинамический процесс, во время которого удельная теплоёмкость c газа остаётся неизменной. Предельными частными явлениями политропного процесса являются изотермический процесс и адиабатный процесс. В случае идеального газа изобарный процесс и изохорный процесс также являются политропическими. Для идеального газа уравнение политропы может быть записано в виде: pVn = const где величина В зависимости от процесса можно определить значение n: 1. Изотермический процесс: n = 1, так как PV 1 = const, значит PV = const, значит T = const. 2. Изобарный процесс: n = 0, так как PV 0 = P = const. 3. Адиабатный процесс: n = γ, это следует из уравнения Пуассона. Здесь γ — показатель адиабаты. 4. Изохорный процесс:
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 606; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.202.58 (0.007 с.) |




 — масса газа,
— масса газа,  — молярная масса газа,
— молярная масса газа,  — молярная теплоёмкость при постоянном объёме,
— молярная теплоёмкость при постоянном объёме,  — давление,объём и температура газа соответственно, причём последнее равенство верно только для идеального газа.
— давление,объём и температура газа соответственно, причём последнее равенство верно только для идеального газа.

 . При изменении объема температура и давление меняются, то есть
. При изменении объема температура и давление меняются, то есть  . Следовательно, теплоемкость идеального газа в адиабатическом процессе также равна нулю: Садиаб=0.
. Следовательно, теплоемкость идеального газа в адиабатическом процессе также равна нулю: Садиаб=0. . При изменении объема газу передается (или отбирается) некоторое количество тепла. Следовательно, теплоемкость идеального газа стремится к бесконечности:
. При изменении объема газу передается (или отбирается) некоторое количество тепла. Следовательно, теплоемкость идеального газа стремится к бесконечности: 
 . Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение (δ A = δ VP). Первое Начало Термодинамики для изохорического процесса имеет вид:
. Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение (δ A = δ VP). Первое Начало Термодинамики для изохорического процесса имеет вид:


 ):
):
 , где
, где  — изменение внутренней энергии тела,
— изменение внутренней энергии тела,  — работа, совершаемая системой,
— работа, совершаемая системой, 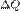 — теплота, полученная системой.
— теплота, полученная системой. , где T - температура системы.
, где T - температура системы.

 ,
, :
: .
.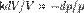 ,
, .
. ,
, , где R — универсальная газовая постоянная
, где R — универсальная газовая постоянная называется показателем политропы.
называется показателем политропы. , так как
, так как  , значит P 1 / P 2 = (V 2 / V 1) n, значит V 2 / V 1 = (P 1 / P 2)(1 / n ), значит, чтобы V 2 / V 1 обратились в 1, n должна быть бесконечность.
, значит P 1 / P 2 = (V 2 / V 1) n, значит V 2 / V 1 = (P 1 / P 2)(1 / n ), значит, чтобы V 2 / V 1 обратились в 1, n должна быть бесконечность.


