
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Материальная точка. Твердое тело. Система отсчета и системы координатСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Материальная точка. Твердое тело. Система отсчета и системы координат Материа́льная то́чка — простейшая физическая модель в механике — математическая абстракция — тело, размеры которого допустимо считать бесконечно малыми по отношению к остальным объектам исследуемой задачи. Практически под материальной точкой понимают обладающее массой тело, размерами и формой которого можно пренебречь при решении данной задачи.[1] Например, при расчёте пути, пройденного поездом, можно пренебречь его размерами, даже если путь измеряется сантиметрами. Механическая энергия может быть запасена материальной точкой лишь в виде кинетической энергии её движения в пространстве, и (или) потенциальной энергии взаимодействия с полем. Это автоматически означает неспособность материальной точки к деформациям (материальной точкой может быть названо лишь абсолютно твёрдое тело) и вращению вокруг собственной оси и изменениям направления этой оси в пространстве Абсолю́тно твёрдое те́ло — второй опорный объект механики наряду с материальной точкой. Механика абсолютно твердого тела полностью сводима к механике материальных точек (с наложенными связями), но имеет собственное содержание (полезные понятия и соотношения, которые могут быть сформулированы в рамках модели абсолютно твердого тела), представляющее большой теоретический и практический интерес. Существует несколько определений: Абсолютно твёрдое тело — модельное понятие классической механики, обозначающее совокупность материальных точек, расстояния между которыми сохраняются в процессе любых движений, совершаемых этим телом. Иначе говоря, абсолютно твердое тело не только не изменяет свою форму, но и сохраняет неизменным распределение массы внутри. Абсолютно твёрдое тело — механическая система, обладающая только поступательными и вращательными степенями свободы. «Твёрдость» означает, что тело не может быть деформировано, то есть телу нельзя передать никакой другой энергии, кроме кинетической энергии поступательного или вращательного движения. Абсолютно твёрдое тело — тело (система), взаимное положение любых точек которого не изменяется, в каких бы процессах оно ни участвовало. Таким образом, положение абсолютно твердого тела полностью определяется, например, положением жестко привязанной к нему декартовой системы координат (обычно ее начало координат делают совпадающим с центром масс твердого тела). В трёхмерном пространстве и в случае отсутствия (других) связей абсолютно твёрдое тело обладает 6 степенями свободы: три поступательных и три вращательных. Исключение составляет двухатомная молекула или, на языке классической механики, твёрдый стержень нулевой толщины. Такая система имеет только две вращательных степени свободы. Абсолютно твёрдых тел в природе не существует, однако в очень многих случаях, когда деформация тела мала и ей можно пренебречь, реальное тело может (приближенно) рассматриваться как абсолютно твёрдое тело без ущерба для задачи. В рамках релятивистской механики понятие абсолютно твёрдого тела внутренне противоречиво, что показывает, в частности,парадокс Эренфеста. Другими словами, модель абсолютно твердого тела вообще говоря совершенно неприменима к случаю быстрых движений (сопоставимых по скорости со скоростью света), а также к случаю очень сильных гравитационных полей [1]. Система отсчёта — это совокупность точки отсчёта, системы координат и системы отсчёта времени, связанных с этой точкой, по отношению к которой изучается движение (или равновесие) каких-либо других материальных точек или тел[1]. Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями x = f 1(t), y = f 2(t), z = f 3(t). Прямоугольная, или Декартова система координат — наиболее простая и поэтому часто используемая система координат на плоскости и в пространстве. Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат. В полярной системе координат положение точки определяется расстояние до центра координат и углом радиус-вектора с осью Ox. Термин «полярные координаты» используется только на плоскости, в пространстве применяются цилиндрические и сферические системы координат.
Первый закон Ньютона и инерциальная система отсчета. Первый закон Ньютона Первый закон механики, или закон инерции (инерция – это свойство тел сохранять свою скорость при отсутствии действияна негодругих тел), как его часто называют, был установлен еще Галилеем. Но строгую формулировку этого закона дал и включил его в число основных законов механики Ньютон. Закон инерции относится к самому простому случаю движения – движению тела,на которое не оказывают воздействия другие тела. Такие тела называются свободными телами. Ответить на вопрос, как движутся свободные тела, не обращаясь к опыту,нельзя. Однако нельзя поставить ни одного опыта, который бы в чистом виде показал, как движется ни с чем не взаимодействующее тело, так как таких тел нет. Как же быть? Имеется лишь один выход. Надо создать для тела условия, при которых влияние внешних воздействий можно делать все меньшим и меньшим, и наблюдать, к чемуэто ведет. Можно, например, наблюдать за движением гладкого камняна горизонтальной поверхности, после того как ему сообщена некоторая скорость. (Притяжение камня к земле уравновешивается действием поверхности,на которую он опирается, и на скорость его движения влияет только трение.) При этом легко обнаружить, что чем более гладкой является поверхность, тем медленнее будет уменьшаться скорость камня. На гладком льду камень скользит весьма долго, заметно не меняя скорость. Трение можно уменьшить до минимумас помощью воздушной подушки – струй воздуха, поддерживающих тело над твердой поверхностью, вдоль которой происходит движение. Этот принциписпользуется в водном транспорте (суда на воздушной подушке). На основеподобных наблюдений можно заключить: если бы поверхность была идеально гладкой, то при отсутствии сопротивления воздуха (в вакууме) камень совсемне менял бы своей скорости. Именно к такому выводу впервые пришел Галилей. С другой стороны, нетрудно заметить, что, когда скорость тела меняется, всегда обнаруживается воздействие на него других тел. Отсюда можно прийти к выводу,что тело, достаточно удаленноеот другихтел и по этой причинене взаимодействующеес ними,движетсяс постояннойскоростью. Движение относительно, поэтому имеет смысл говорить лишь о движении тела по отношению к системе отсчета, связанной с другим телом. Сразу же возникает вопрос: будет ли свободное тело двигаться с постоянной скоростью по отношению к любому другому телу? Ответ, конечно, отрицательный. Так, если по отношению к Земле свободное тело движется прямолинейно и равномерно, то по отношению к вращающейся карусели тело заведомо так двигаться не будет. Наблюдения за движениями тел и размышления о характере этих движений приводят нас к заключению о том, что свободные тела движутся с постояннойскоростью, по крайней мере, по отношению к определенным телам и связаннымс ними системам отсчета. Например, по отношению к Земле. В этом состоит главное содержание закона инерции. Поэтому первый закон Ньютона может быть сформулирован так: существуют такие системы отсчета, относительно которых тело (материальная точка) при отсутствии на неё внешних воздействий (или при их взаимнойкомпенсации) сохраняет состояние покоя или равномерного прямолинейного движения. Инерциальная система отсчета Первый закон Ньютона утверждает (которое с той или иной степенью точности можно проверить на опыте) о том, что инерциальные системы существуютв действительности. Этот закон механики ставит в особое, привилегированное положение инерциальные системы отсчета. Системы отсчета,в которыхвыполняется первый закон Ньютона, называют инерциальными. Или Инерциальные системы отсчета – это системы, относительно которых материальная точка при отсутствиина неевнешних воздействий илиих взаимнойкомпенсации покоится или движется равномернои прямолинейно. Инерциальных систем существует бесконечное множество. Система отсчета, связанная с поездом, идущим с постоянной скоростью по прямолинейному участку пути, – тоже инерциальная система (приближенно), как и система,связанная с Землей. Все инерциальные системы отсчета образуют класс систем, которые движутся друг относительно друга равномерно и прямолинейно.Ускорения какого-либо тела в разных инерциальных системах одинаковы. Как установить, что данная система отсчета является инерциальной? Это можносделать только опытным путем. Наблюдения показывают, что с очень высокой степенью точности можно считать инерциальной системой отсчета гелиоцентрическую систему, у которой начало координат связано с Солнцем,а оси направлены на определенные «неподвижные» звезды. Системы отсчета, жестко связанные с поверхностью Земли, строго говоря, не являютсяинерциальными, так как Земля движется по орбите вокруг Солнца и при этом вращается вокруг своей оси. Однако при описании движений, не имеющихглобального (т. е. всемирного) масштаба, системы отсчета, связанные с Землей,можно с достаточной точностью считать инерциальными. С гораздо большей точностью можно считать инерциальной систему отсчета,в которой начало координат совмещено с центром Солнца, а координатные оси направлены к неподвижным звездам. Эту систему отсчета называют гелиоцентрической. Инерциальными являютсяи системыотсчета, которые движутся равномернои прямолинейноотносительнокакой-либоинерциальной системы отсчета. Галилей установил, что никакими механическими опытами, поставленными внутри инерциальной системы отсчета, невозможно установить, покоится эта система или движется равномернои прямолинейно. Это утверждение носит название принципа относительности Галилея или механического принципа относительности. Этот принцип был впоследствии развит А. Эйнштейном и является однимиз постулатов специальной теории относительности. Инерциальные системы отсчета играют в физике исключительно важную роль, так как, согласно принципу относительности Эйнштейна, математическое выражение любою закона физики имеет одинаковый вид в каждой инерциальной системе отсчета.В дальнейшем мы будем пользоваться только инерциальными системами(не упоминая об этом каждый раз). Системы отсчета,в которыхпервый закон Ньютонане выполняется,называют неинерциальными. К таким системам относится любая система отсчета, движущаяся с ускорениемотносительно инерциальной системы отсчета. В механике Ньютона законы взаимодействия тел формулируются для класса инерциальных систем отсчета. Примером механического эксперимента, в котором проявляется неинерциальность системы, связанной с Землей, служит поведение маятника Фуко. Так называетсямассивный шар, подвешенный на достаточно длинной нити и совершающий малые колебания около положения равновесия. Если бы система, связанная с Землей,была инерциальной, плоскость качаний маятника Фуко оставалась бы неизменной относительно Земли. На самом деле плоскость качаний маятника вследствие вращения Земли поворачивается, и проекция траектории маятникана поверхность Земли имеет вид розетки (рис. 1).
Рис. 1. О том, что телу свойственно сохранять не любое движение, а именнопрямолинейное, свидетельствует, например, следующий опыт (рис. 2). Шарик, двигавшийся прямолинейно по плоской горизонтальной поверхности, сталкиваясьс преградой, имеющей криволинейную форму, под действием этой преграды вынужден двигаться по дуге. Однако когда шарик доходит до края преграды,он перестает двигаться криволинейно и вновь начинает двигаться по прямой. Обобщая результаты упомянутых (и аналогичных им) наблюдений, можно сделать вывод, что еслинаданноетелонедействуютдругиетелаилиихдействиявзаимнокомпенсируются, этотелопокоитсяилижескоростьегодвиженияостаетсянеизменнойотносительносистемыотсчета, неподвижносвязаннойсповерхностьюЗемли.
Третий закон Ньютона. Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой Современная формулировка
Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами. Историческая формулировка
Физический смысл работы Работавсех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:
Теорема Кёнига (механика) Кинетическая энергия системы есть энергия движения центра масс плюс энергия движения относительно центра масс:
где T — полная кинетическая энергия, Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы впоступательном движении и энергии системы во вращательном движении относительно центра масс.
Пусть — радиус-вектор рассматриваемой точки в подвижной системе координат. Тогда:
Если
Вычислим полную кинетическую энергию системы в случае, если начало координат подвижной системы помещено в её центр масс. С учетом предыдущего соотношения:
Раскрывая скобки и вынося из-под знака интеграла, получаем:
Третий член равен Tr, введённой ранее относительной энергии системы. Теорема о кинетической энергии для системы частиц. Теорема об изменении кинетической энергии системы: в дифференциальной форме: dT = Т2 – Т1=
Определение Момент импульса
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с. Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:
Замечание: в принципе момент импульса может быть вычислен относительно любого начала отсчета (получившиеся при этом разные значения связаны очевидным образом); однако чаще всего (для удобства и определенности) его вычисляют относительно центра масс или закрепленной точки вращения твердого тела итп). Вычисление момента Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам
где Запишем
Импульсом системы N материальных точек называется векторная сумма импульсов отдельных материальных точек образующих данную систему.
Осевой момент инерции
Осевые моменты инерции некоторых тел. Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: § mi — масса i -й точки, § ri — расстояние от i -й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности впоступательном движении.
где: § dm = ρ dV — масса малого элемента объёма тела dV, § ρ — плотность, § r — расстояние от элемента dV до оси a. Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Штейнера
Вывод Момент инерции, по определению:
Радиус-вектор
где
Вынося за сумму
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:
Тогда:
Откуда и следует искомая формула:
где JC — известный момент инерции относительно оси, проходящей через центр масс тела.
Виды колебаний § Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание). § Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (т.е. чтобы зависимость от времени этой силы была синусоидальной).
Или Кинетическая энергия:
Потенциальная энергия:
Учитывая то, что
Полная энергия колеблющегося тела равна сумме кинетической и потенциальной энергий
Связь между угловыми и линейными скоростями и ускорениями. Так как d r /dt= v и d(фи)/dt= w, то v =[d(фи)/dt, r ]=[ w, r ](1),т.е. линейная скорость v точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению угловой скорости w на радиус- вектор r точки. Модуль вектора равен v = wr sin(тэтта) или v = w R, где R = r sin(тэтта) – радиус окружности, по которой движется точка. Направление вектора v совпадает с направлением поступательного движения буравчика (правило правого винта) при его вращении от w к r. Если мы продифференцируем ур-ние (1) по времени, то найдём полное ускорение точки: a =[d w /dt, r ]+[ w,d r /dt]=[(бетта), r ]+[ w, v ]= [(бетта), r] +[ w,[ w, r ]]. При равноускоренном вращательном движении (бетта) = const) можно показать, что модуль полного ускорения точки есть величина a=rad(a2t+a2n), где все векторы a, at и an лежат в плоскости, перпендикулярной оси вращения. В этом случае справедливы формулы: an =v2/R=w2R, at =dv/dt=d(wR)/dt=R*(бетта), s=t2&t1vdt=t2&t1wRdt=R t2&t1d(фи)/dt*dt=R(фи) где s –длина пути, пройденного точкой по дуге окружности радиуса R; (фи) – угол поворота за промежуток времени (t2-t1). Решения
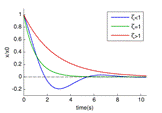
Зависимость графиков колебаний от значения ζ. В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта. § Апериодичность Если
В этом случае колебания с самого начала экспоненциально затухают. § Граница апериодичности Если
В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание. § Слабое затухание Если
Тогда решением исходного дифференциального уравнения является
Где Константы c 1 и c 2 в каждом из случаев определяются из начальных условий:
Уравнение плоской волны. Пусть в начале координат находится твердая плоскость, которая колеблется по гармоническому закону и вынуждает частицы упругой среды, находящейся рядом с ней, колебаться по этому же закону. Направим ось x перпендикулярно этой плоскости. Тогда вдоль этой оси будет распространяться плоская гармоническая продольная волна. Наша задача - найти
Колебания до волновой поверхности, удаленной от начала координат на расстояние x, дойдут через время
Фаза волны - это аргумент у косинуса в уравнении волны, т.е.
Фаза плоской волны зависит от двух переменных - x и t. Фазовая скорость - это скорость перемещения в пространстве поверхности, вдоль которой фаза волны (15.2.1) остается постоянной, т.е.
Найдем производную от этого выражения по времени:
откуда искомая фазовая скорость волны:
Уравнение плоской волны, распространяющейся в направлении, противоположном оси x:
Из (15.2.2) для этой волны:
Скорость волны. Механические волны — это распространяющиеся в упругой среде возмущения (отклонения частиц среды от положения равновесия). Если колебания частиц и распространение волны происходят в одном направлении, волну называют продольной, а если эти движения происходят в перпендикулярных направлениях, — поперечной. Продольные волны, сопровождаемые деформациями растяжения и сжатия, могут распространяться в любых упругих средах: газах, жидкостях и твердых телах. Поперечные волны распространяются в тех средах, где появляются силы упругости при деформации сдвига, т. е. в твердых телах. При распространении волны происходит перенос энергии без переноса вещества. Скорость, с которой распространяется возмущение в упругой среде, называют скоростью волны* Она определяется упругими свойствами среды. Расстояние, на которое распространяется волна за время, равное периоду колебаний в ней (Г), называется длиной волны l (ламбда).
ИЛИ Зафиксируем какое-либо значение фазы, стоящей в уравнении (2.2), положив ее постоянной для данной точки
Это выражение дает связь между временем t и координатой х, в которой зафиксированное значение фазы осуществляется в данный момент. Определив
Откуда
Таким образом, скорость распространения волны V в уравнении (2.2) есть скорость перемещения фазы, в связи с чем ее называют фазовой скоростью.
Виды теплообмена Всего существует три простых (элементарных) вида передачи тепла: § Теплопроводность § Конвекция § Тепловое излучение
Адиабатический В адиабатическом процессе теплообмена с окружающей средой не происходит, то есть Изотермический В изотермическом процессе постоянна температура, то есть Изохорный В изохорическом процессе постоянен объем, то есть
А для идеального газа
Таким образом,
где i — число степеней свободы частиц газа. Изобарный В изобарном процессе (
CP=δQ/νΔT=CV+R=((i+2)/2)*R Вывод уравнения Согласно закону Менделеева — Клапейрона[5]:
Продифференцировав обе части, получаем:
Если в (3) подставить dT из (2), а затем dU из (1), получим:
или, введя коэффициент
Или
что после интегрирования даёт:
Окончательно имеем,
что и требовалось доказать. При адиабатическом процессе показатель адиабаты равен Политропный процесс — термодинамический процесс, во время которого удельная теплоёмкость c газа остаётся неизменной. Предельными частными явлениями политропного процесса являются изотермический процесс и адиабатный процесс. В случае идеального газа изобарный процесс и изохорный процесс также являются политропическими. Для идеального газа уравнение политропы может быть записано в виде: pVn = const где величина В зависимости от процесса можно определить значение n: 1. Изотермический процесс: n = 1, так как PV 1 = const, значит PV = const, значит T = const. 2. Изобарный процесс: n = 0, так как PV 0 = P = const. 3. Адиабатный процесс: n = γ, это следует из уравнения Пуассона. Здесь
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1116; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.69.167 (0.013 с.) |



 , а второе — на первое с силой
, а второе — на первое с силой  . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
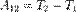
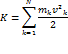
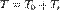 ,
, — энергия движения центра масс,
— энергия движения центра масс,  — относительная кинетическая энергия.
— относительная кинетическая энергия.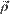 Выразим относительную кинетическую энергию Tr системы S как энергию, вычисленной относительно подвижной системы координат.
Выразим относительную кинетическую энергию Tr системы S как энергию, вычисленной относительно подвижной системы координат.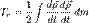
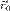 — радиус-вектор начала координат подвижной системы, а
— радиус-вектор начала координат подвижной системы, а  — радиус-вектор рассматриваемой точки в исходной системе координат, то верно соотношение:
— радиус-вектор рассматриваемой точки в исходной системе координат, то верно соотношение: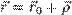
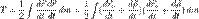
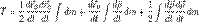
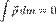 Первое слагаемое представляет собой кинетическую энергию материальной точки, помещённой в начало координат подвижной системы и имеющей массу, равную массе этой системы. Второй член равен нулю, так как по предположению начало координат подвижной системы помещено в её центр масс, следовательно,
Первое слагаемое представляет собой кинетическую энергию материальной точки, помещённой в начало координат подвижной системы и имеющей массу, равную массе этой системы. Второй член равен нулю, так как по предположению начало координат подвижной системы помещено в её центр масс, следовательно,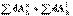 ,
,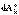 ,
, 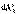 – элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме:
– элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме: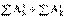 . Для неизменяемой системы
. Для неизменяемой системы 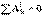 и Т2 – Т1=
и Т2 – Т1=  , т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными.
, т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными.
 частицы относительно некоторого начала отсчёта определяетсявекторным произведением её радиус-вектора и импульса:
частицы относительно некоторого начала отсчёта определяетсявекторным произведением её радиус-вектора и импульса:
 где
где  — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, — импульс частицы.
— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, — импульс частицы.
 где
где  — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется. где
где  - импульс бесконечно малого точечного элемента системы).
- импульс бесконечно малого точечного элемента системы). .
. и. Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения. Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на неё можно указать ряд рецептов в соответствии с общими правилами нахождения векторного произведения двух векторов.
и. Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения. Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на неё можно указать ряд рецептов в соответствии с общими правилами нахождения векторного произведения двух векторов.
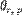 — угол между
— угол между  и
и  , определяемый так, чтобы поворот от
, определяемый так, чтобы поворот от  , где
, где 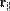 — составляющая радиус-вектора, параллельная вектору импульса, а
— составляющая радиус-вектора, параллельная вектору импульса, а  — аналогично,перпендикулярная ему.
— аналогично,перпендикулярная ему.  является, по сути, расстоянием от оси вращения до вектора
является, по сути, расстоянием от оси вращения до вектора  , которое обычно называют «плечом». Аналогично можно разделить вектор импульса на две составляющие: параллельную радиус-вектору
, которое обычно называют «плечом». Аналогично можно разделить вектор импульса на две составляющие: параллельную радиус-вектору  и перпендикулярную ему
и перпендикулярную ему  . Теперь, используя линейность векторного произведения, а также свойство, согласно которому произведение параллельных векторов равно нулю, можно получить еще два выражения для
. Теперь, используя линейность векторного произведения, а также свойство, согласно которому произведение параллельных векторов равно нулю, можно получить еще два выражения для  .
.

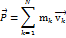

 ,
, ,
,


 можно расписать как разность двух векторов:
можно расписать как разность двух векторов: ,
, — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:
— радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:
 , получим:
, получим:


 ,
,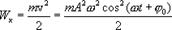
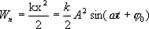
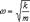 т.е.,
т.е., 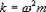 последнее выражение можно записать в виде:
последнее выражение можно записать в виде: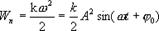


 , то имеется два действительных корня, и решение дифференциального уравнения принимает вид:
, то имеется два действительных корня, и решение дифференциального уравнения принимает вид:
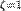 , два действительных корня совпадают
, два действительных корня совпадают  , и решением уравнения является:
, и решением уравнения является:
 , то решением характеристического уравнения являются два комплексно сопряжённых корня
, то решением характеристического уравнения являются два комплексно сопряжённых корня
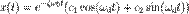
 — собственная частота затухающих колебаний.
— собственная частота затухающих колебаний.
 - уравнение волны, если задано
- уравнение волны, если задано  .
.
 , значит уравнение волны
, значит уравнение волны .
. ,
, .
. ,
, .
. .
. .
.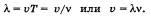

 , мы найдем скорость, с которой перемещается данное значение фазы. Дифференцируя это соотношение, получим
, мы найдем скорость, с которой перемещается данное значение фазы. Дифференцируя это соотношение, получим
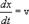
 . При изменении объема температура и давление меняются, то есть
. При изменении объема температура и давление меняются, то есть  . Следовательно, теплоемкость идеального газа в адиабатическом процессе также равна нулю: Садиаб=0.
. Следовательно, теплоемкость идеального газа в адиабатическом процессе также равна нулю: Садиаб=0. . При изменении объема газу передается (или отбирается) некоторое количество тепла. Следовательно, теплоемкость идеального газа стремится к бесконечности:
. При изменении объема газу передается (или отбирается) некоторое количество тепла. Следовательно, теплоемкость идеального газа стремится к бесконечности: 
 . Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение (δ A = δ VP). Первое Начало Термодинамики для изохорического процесса имеет вид:
. Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение (δ A = δ VP). Первое Начало Термодинамики для изохорического процесса имеет вид:


 ):
):


 ,
, :
: .
.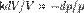 ,
, .
. ,
, , где R — универсальная газовая постоянная
, где R — универсальная газовая постоянная называется показателем политропы.
называется показателем политропы.


