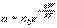Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение Максвелла. Средняя, среднеквадратичная и наивероятнейшая скорости молекул.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Распределение по модулю скоростей Обычно, более интересно распределение по абсолютному значению, а не по проекциям скоростей молекул. Модуль скорости, v определяется как:
поэтому модуль скорости всегда будет больше или равен нулю. Так как все где
таким образом, функция плотности вероятности для модуля скорости равна
.Вывод распределения по Максвеллу Получим теперь формулу распределения так, как это делал сам Джеймс Клерк Максвелл[ источник не указан 563 дня ].
Максвелл предположил, что распределения скоростей по направлениям статистически независимы, то есть компонента
Правая часть не зависит от
Теперь нужно сделать принципиальный шаг - ввести температуру. Кинетическое определение температуры (как меры средней кинетической энергии движения молекул):
где
Все направления равноправны:
Чтобы найти среднее значение
Отсюда найдём
Функция распределения плотности вероятности для
Рассмотрим теперь распределение по величине скорости. Вернемся в пространство скоростных точек. Все точки с модулем скорости
Так, мы получили Наиболее вероятная скорость наиболее вероятная скорость,
Средняя скорость
Подставляя
Среднеквадратичная скорость
Подставляя
Обратимые и необратимые процессы, примеры. Второе начало термодинамики. Тепловые процессы можно разделить на обратимые и необратимые. Обратимым называется процесс, который можно провести в противоположном направлении через все те же самые промежуточные состояния. Обратимый процесс (то есть равновесный) — термодинамический процесс, который может проходить как в прямом, так и в обратном направлении, проходя через одинаковые промежуточные состояния, причем система возвращается в исходное состояние без затрат энергии, и в окружающей среде не остается макроскопических изменений. Обратимый процесс можно в любой момент заставить протекать в обратном направлении, изменив какую-либо независимую переменную на бесконечно малую величину. Понятия равновесного состояния и обратимого процесса играют большую роль в термодинамике. Все количественные выводы термодинамики применимы только к равновесным состояниям и обратимым процессам. Необратимым называется процесс, который нельзя провести в противоположном направлении через все те же самые промежуточные состояния. Все реальные процессы необратимы. Примеры необратимых процессов: диффузия, термодиффузия,теплопроводность, вязкое течение и др. Переход кинетической энергии макроскопического движения через трение в теплоту, то есть во внутреннюю энергию системы, является необратимым процессом. «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему» [ Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не должна равняться 0. Распределение частиц во внешнем силовом поле (распределение Больцмана). При рассмотрении кинетической теории газов и закона распределения Максвелла предполагалось, что на молекулы газа не действуют никакие силы, за исключением ударов молекул. Поэтому, молекулы равномерно распределяются по всему сосуду. В действительности молекулы любого газа всегда находятся в поле тяготения Земли. Вследствие этого, каждая молекула массой m испытывает действие силы тяжести f =mg.
Выделим горизонтальный элемент объема газа высотой dh и площадью основания S (рис. 11.2). Считаем газ однородным и температуру его постоянной. Число молекул в этом объеме равно произведению его объема dV=Sdh на число молекул
Действие веса dF вызывает давление, равное
минус - т.к. при увеличении dh давление уменьшается. Согласно основному уравнению молекулярно-кинетической теории
Приравнивая правые части (11.2) и (11.3), получаем
Интегрируя это выражение в пределах от
Потенцируя полученное выражение, находим
Показатель степени при exp имеет множитель
Тогда уравнение для концентрации молекул преобразуется к виду
Это уравнение отображает общий закон Больцмана и дает распределение числа частиц в зависимости от их потенциальной энергии. Он применим к любой системе частиц, находящихся в силовом поле, например в электрическом.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 767; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |

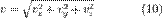
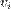 распределены нормально, то
распределены нормально, то 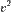 будет иметь хи-квадрат распределение с тремя степенями свободы. Если
будет иметь хи-квадрат распределение с тремя степенями свободы. Если 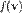 — функция плотности вероятности для модуля скорости, то:
— функция плотности вероятности для модуля скорости, то:  ,
,
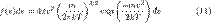
 ) встационарном состоянии газа. Выберем бесконечно малый элемент объема
) встационарном состоянии газа. Выберем бесконечно малый элемент объема  . Так как газ стационарный, количество скоростных точек в
. Так как газ стационарный, количество скоростных точек в  остается неизменным с течением времени. Пространство скоростей изотропно, поэтому функцииплотности вероятности для всех направлений одинаковы.
остается неизменным с течением времени. Пространство скоростей изотропно, поэтому функцииплотности вероятности для всех направлений одинаковы.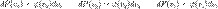
 скорости молекулы не зависит от
скорости молекулы не зависит от 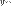 и
и  компонент.
компонент.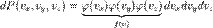 - фактически вероятность нахождения скоростной точки в объеме
- фактически вероятность нахождения скоростной точки в объеме 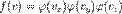
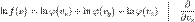


 и
и 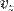 , значит и левая от
, значит и левая от  и
и 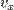 и
и 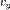 равноправны, значит левая часть не зависит также и от
равноправны, значит левая часть не зависит также и от 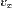 . Значит, это константа.
. Значит, это константа.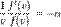


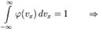
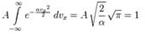

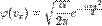

 Дж/К - постоянная Больцмана.
Дж/К - постоянная Больцмана.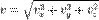
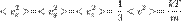
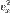 , проинтегрируем её вместе с функцией плотности вероятности от минус до плюс бесконечности:
, проинтегрируем её вместе с функцией плотности вероятности от минус до плюс бесконечности: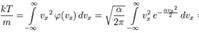
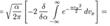
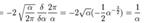
 :
:
 (для
(для  и
и  аналогично):
аналогично):
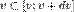 лежат в шаровом слое радиуса
лежат в шаровом слое радиуса 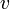 и толщины
и толщины 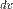 , и
, и 
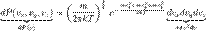

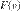 - функцию плотности вероятности, которая и называется распределением Максвелла.
- функцию плотности вероятности, которая и называется распределением Максвелла. — вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению
— вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению 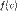 . Чтобы найти её, необходимо вычислить
. Чтобы найти её, необходимо вычислить 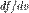 , приравнять её нулю и решить относительно
, приравнять её нулю и решить относительно 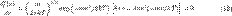
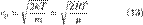

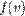 и интегрируя, мы получим
и интегрируя, мы получим

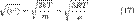
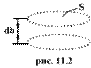
 в единице объема. Полный вес молекул в выделенном элементе равен
в единице объема. Полный вес молекул в выделенном элементе равен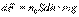

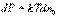
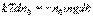

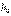 до h (соответственно концентрация изменяется от
до h (соответственно концентрация изменяется от 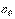 до n):
до n):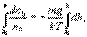
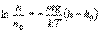
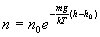
 , который определяет приращение потенциальной энергии молекул газа. Если переместить молекулу с уровня
, который определяет приращение потенциальной энергии молекул газа. Если переместить молекулу с уровня 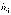 до уровня h, то изменение ее потенциальной энергии будет
до уровня h, то изменение ее потенциальной энергии будет