
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент импульса твердого тела относительно неподвижной оси.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена МОМЕНТ ИМПУЛЬСА МАТЕРИАЛЬНОЙ ТОЧКИ Момент импульса материальной точки относительно точки O определяется векторным произведением Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса): Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело:
Кинетическая энергия тела, вращающегося вокруг неподвижной оси, и при плоском движении. Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:
Если тело вращается вокруг неподвижной оси с угловой скоростью
где Выведем уравнение для кинетической энергии твердого тела при плоском движении. Пусть тело совершает плоское движение в некоторой инерциальной K-системе отсчета. Чтобы найти его кинетическую энергию Т в этой системе, воспользуемся формулой (5.12). Входящая в эту формулу величина
где Таким образом, кинетическая энергия твердого тела при плоском движении складывается из энергии вращения в С-системе и энергии, связанной с движением центра масс.
Момент инерции и его свойства. Теорема Штейнера. Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движениивокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения СИ: кг·м². Обозначение: I или J. Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек. Осевой момент инерции
Осевые моменты инерции некоторых тел. Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: § mi — масса i -й точки, § ri — расстояние от i -й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности впоступательном движении.
где: § dm = ρ dV — масса малого элемента объёма тела dV, § ρ — плотность, § r — расстояние от элемента dV до оси a. Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Штейнера
Вывод Момент инерции, по определению:
Радиус-вектор
где
Вынося за сумму
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:
Тогда:
Откуда и следует искомая формула:
где JC — известный момент инерции относительно оси, проходящей через центр масс тела.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 2203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 , где
, где  — радиус-вектор, проведенный из точки O,
— радиус-вектор, проведенный из точки O,  — импульс материальной точки.
— импульс материальной точки. равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса
равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса  не зависит от положения точки O на оси z.
не зависит от положения точки O на оси z. , получим
, получим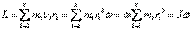 .
. .
. .
.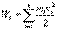
 , то линейная скорость i-ой точки равна
, то линейная скорость i-ой точки равна  , где
, где 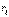 , - расстояние от этой точки до оси вращения. Следовательно.
, - расстояние от этой точки до оси вращения. Следовательно.
 - момент инерции тела относительно оси вращения.
- момент инерции тела относительно оси вращения. в данном случае представляет собой кинетическую энергию вращения тела в С-системе вокруг оси, проходящей через центр масс тела. Согласно (6.31)
в данном случае представляет собой кинетическую энергию вращения тела в С-системе вокруг оси, проходящей через центр масс тела. Согласно (6.31) 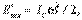 поэтому сразу можно записать
поэтому сразу можно записать
 - момент инерции тела относительно оси вращения, проходящей через его центр масс,
- момент инерции тела относительно оси вращения, проходящей через его центр масс,  -угловая скорость тела, т - его масса,
-угловая скорость тела, т - его масса,  - скорость центра инерции тела в K-системе отсчета
- скорость центра инерции тела в K-системе отсчета
 ,
, ,
,


 можно расписать как разность двух векторов:
можно расписать как разность двух векторов: ,
, — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:
— радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:
 , получим:
, получим:


 ,
,


