
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центр масс. Уравнение движения центра масс. Система центра масс.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Центр масс (центр ине́рции; барице́нтр от др.-греч. βαρύς «тяжёлый» и κέντρον «центр») в механике — это геометрическая точка, характеризующая движение тела или системы частиц как целого. Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:
где
Для случая непрерывного распределения масс:
где:
. Уравнение движения центра масс
Систе́ма це́нтра масс (систе́ма це́нтра ине́рции) — невращающаяся система отсчёта, связанная с центром масс механической системы. Обычно сокращается как с. ц. м. или с. ц. и. Суммарный импульс системы в с.ц.м. равен нулю. Для замкнутой системы её система центра масс инерциальна, тогда как незамкнутая система в общем случае может обладать неинерциальной системой центра масс. Суммарная кинетическая энергия механической системы в с.ц.м. минимальна среди всех систем отсчёта; в любой другой невращающейся (не обязательно инерциальной) системе отсчёта кинетическая энергия равна кинетической энергии в с.ц.м. плюс кинетическая энергия движения механической системы как целого (MV ²/2, где М — полная масса механической системы, V — относительная скорость движения систем отсчёта).
Работа переменной силы. Мощность. Кинетическая энергия частицы и системы частиц. Теорема Кенига.
Работа равна сумме работ(адитивная величина) Аддитивность (лат. additivus — прибавляемый) — свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, в некотором классе возможных разбиений объекта на части. Например, аддитивность объёма означает, что объём целого тела равен сумме объёмов составляющих его часте Мо́щность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:
где:
Физический смысл работы Работавсех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:
Теорема Кёнига (механика) Кинетическая энергия системы есть энергия движения центра масс плюс энергия движения относительно центра масс:
где T — полная кинетическая энергия, Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы впоступательном движении и энергии системы во вращательном движении относительно центра масс.
Пусть — радиус-вектор рассматриваемой точки в подвижной системе координат. Тогда:
Если
Вычислим полную кинетическую энергию системы в случае, если начало координат подвижной системы помещено в её центр масс. С учетом предыдущего соотношения:
Раскрывая скобки и вынося из-под знака интеграла, получаем:
Третий член равен Tr, введённой ранее относительной энергии системы. Теорема о кинетической энергии для системы частиц. Теорема об изменении кинетической энергии системы: в дифференциальной форме: dT = Т2 – Т1=
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.210 (0.007 с.) |

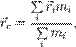
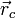 — радиус-вектор центра масс,
— радиус-вектор центра масс,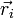 — радиус-вектор i -й точки системы,
— радиус-вектор i -й точки системы,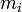 — масса i -й точки.
— масса i -й точки.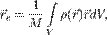

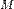 — суммарная масса системы,
— суммарная масса системы, — объём,
— объём, — плотность.
— плотность.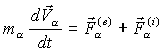

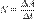

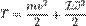
 — масса тела
— масса тела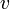 — скорость центра масс тела
— скорость центра масс тела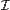 — момент инерции тела
— момент инерции тела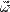 — угловая скорость тела.
— угловая скорость тела.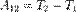
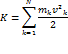
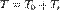 ,
, — энергия движения центра масс,
— энергия движения центра масс,  — относительная кинетическая энергия.
— относительная кинетическая энергия.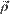 Выразим относительную кинетическую энергию Tr системы S как энергию, вычисленной относительно подвижной системы координат.
Выразим относительную кинетическую энергию Tr системы S как энергию, вычисленной относительно подвижной системы координат.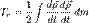
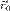 — радиус-вектор начала координат подвижной системы, а
— радиус-вектор начала координат подвижной системы, а  — радиус-вектор рассматриваемой точки в исходной системе координат, то верно соотношение:
— радиус-вектор рассматриваемой точки в исходной системе координат, то верно соотношение: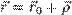
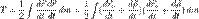
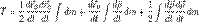
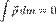 Первое слагаемое представляет собой кинетическую энергию материальной точки, помещённой в начало координат подвижной системы и имеющей массу, равную массе этой системы. Второй член равен нулю, так как по предположению начало координат подвижной системы помещено в её центр масс, следовательно,
Первое слагаемое представляет собой кинетическую энергию материальной точки, помещённой в начало координат подвижной системы и имеющей массу, равную массе этой системы. Второй член равен нулю, так как по предположению начало координат подвижной системы помещено в её центр масс, следовательно,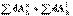 ,
,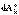 ,
, 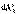 – элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме:
– элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме: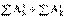 . Для неизменяемой системы
. Для неизменяемой системы 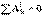 и Т2 – Т1=
и Т2 – Т1=  , т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными.
, т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными.



