
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон всемирного тяготения. Сила тяжести и вес. Упругие силы. Силы реакции, силы сухого и вязкого трения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В рамках классической механики гравитационное взаимодействие описывается законом всемирного тяготения. Этот закон был открыт Ньютоном в 1666 г.. Он гласит, что сила гравитационного притяжения между двумя материальными точками массы m 1 и m 2, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:
Здесь G — гравитационная постоянная, равная СИЛА ТЯЖЕСТИ, сила P, действующая на любое тело, находящееся вблизи земной поверхности, и определяемая как геометрическая сумма силы притяжения Земли F и центробежной силы инерции Q, учитывающей эффект суточного вращения Земли. Направление силы тяжести - вертикаль в данной точке земной поверхности. Аналогично определяется сила тяжести на любом небесном теле. Значение силы тяжести зависит от географической широты положения тела; например, на Земле сила тяжести на полюсе и на экваторе отличаются на 0,5% (на Луне значения силы тяжести примерно в 6 раз меньше, чем на Земле; смотри Ускорение свободного падения). Частным видом силы всемирного тяготения является сила притяжения тел к Земле (или к другой планете). Эту силу называют силой тяжести. Под действием этой силы все тела приобретают ускорение свободного падения. В соответствии со вторым законом Ньютона g = Ft*m следовательно, Ft = mg. Сила тяжести всегда направлена к центру Земли. В зависимости от высоты h над поверхностью Земли и географической широты положения тела ускорение свободного падения приобретает различные значения. На поверхности Земли и в средних широтах ускорение свободного падения равно 9,831 м/с2. Деформация называется упругой, если после снятия внешнего воздействия тело возвращается в исходное состояние. При небольших деформациях растяжения или сжатия х сила упругости прямо пропорциональна деформации и направлена в сторону противоположную ей. Fупр = – kx, где k – коэффициент упругости, зависящий от свойств материала и геометрии деформируемого тела. Сила упругости препятствует деформации. Для характеристики упругих свойств вещества вводиться величина E, называемая модулем Юнга. Напряжение σ, возникающие в твердом теле, равно σ=F/S, где S площадь поперечного сечения твердого тела, на которое воздействует сила F. Относительная деформация ε=x/l0, где l0 – длина тела до деформации пропорциональна напряжению, возникающему в твёрдом теле (закон Гука). ε=(1/E)σ. Физический смысл модуля Юнга состоит в следующем: величина E численно равна напряжению, возникшему в твердом теле при относительной деформации, равной единице. Из физического смысла модуля Юнга следует, что E является большим по величине. 3. Силы трения. Сила трения покоя
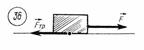
Сила трения скольжения. Прикрепим динамометр к бруску и заставим брусок двигаться равномерно по горизонтальной поверхности стола. Во время равномерного движения бруска динамометр показывает, что на брусок со стороны пружины действует постоянная сила упругости Вектор силы трения скольжения Природа силы трения. Силы трения возникают благодаря существованию сил взаимодействия между молекулами и атомами соприкасающихся тел. Последние обусловлены взаимодействием электрических зарядов, которыми обладают частицы, входящие в состав атомов. Коэффициент трения. Исследуем, от чего зависит сила трения. Для этого воспользуемся гладкой деревянной доской, деревянным бруском и динамометром (рис. 37).
Сначала проверим, зависит ли сила трения от площади поверхности соприкосновения тел. Положим брусок на горизонтально расположенную доску гранью с самой большой площадью поверхности. Прикрепив к бруску динамометр, будем плавно увеличивать силу, направленную вдоль поверхности доски, и заметим максимальное значение силы трения покоя. Затем поставим тот же брусок на другую грань с меньшей площадью поверхности и вновь измерим максимальное значение силы трения покоя. Опыт показывает, что максимальное значение силы трения покоя не зависит от площади поверхности соприкосновения тел. Повторив такие же измерения при равномерном движении бруска по поверхности доски, убеждаемся, что сила трения скольжения также не зависит от площади поверхности соприкосновения тел. Поставим на первый брусок второй такой же. Этим мы увеличим силу, перпендикулярную поверхности соприкосновения тела и стола (ее называют силой давления На основании таких опытов можно сделать вывод, что максимальное значение модуля силы трения покоя прямо пропорционально силе давления. Взаимодействие тела и опоры вызывает деформацию и тела, и опоры. Силу упругости
По третьему закону Ньютона сила давления и сила реакции опоры равны по модулю и противоположны по направлению:
Поэтому предыдущий вывод можно сформулировать так: модуль максимальной силы трения покоя пропорционален силе реакции опоры:
Греческой буквой Опыт показывает, что модуль силы трения скольжения
Максимальное значение силы трения покоя примерно равно силе трения скольжения, приближенно равны также коэффициенты трения покоя и скольжения. Силы трения возникают и при качении тела. При одинаковой нагрузке сила трения качения значительно меньше силы трения скольжения. Поэтому для уменьшения сил трения в технике применяются колеса, шариковые и роликовые подшипники.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 519; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.40.171 (0.008 с.) |


 м³/(кг с²).
м³/(кг с²).



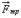 равна по модулю внешней силе
равна по модулю внешней силе  , направленной по касательной к поверхности соприкосновения тел, и противоположна ей по направлению (рис. 36):
, направленной по касательной к поверхности соприкосновения тел, и противоположна ей по направлению (рис. 36): .
.
 . При равномерном движении бруска равнодействующая всех сил, приложенных к нему, равна нулю. Следовательно, кроме силы упругости, во время равномерного движения на брусок действует сила, равная по модулю силе упругости, но направленная в противоположную сторону. Эта сила называется силой трения скольжения
. При равномерном движении бруска равнодействующая всех сил, приложенных к нему, равна нулю. Следовательно, кроме силы упругости, во время равномерного движения на брусок действует сила, равная по модулю силе упругости, но направленная в противоположную сторону. Эта сила называется силой трения скольжения 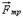 .
. всегда направлен противоположно вектору скорости
всегда направлен противоположно вектору скорости  движения тела относительно соприкасающегося с ним тела. Поэтому действие силы трения скольжения всегда приводит к уменьшению модуля относительной скорости тел.
движения тела относительно соприкасающегося с ним тела. Поэтому действие силы трения скольжения всегда приводит к уменьшению модуля относительной скорости тел.
 ). Если теперь мы вновь измерим максимальную силу трения покоя (рис. 38), то увидим, что она увеличилась в два раза. Поставив на два бруска третий, обнаруживаем, что максимальная сила трения покоя увеличилась в три раза.
). Если теперь мы вновь измерим максимальную силу трения покоя (рис. 38), то увидим, что она увеличилась в два раза. Поставив на два бруска третий, обнаруживаем, что максимальная сила трения покоя увеличилась в три раза. , возникающую в результате деформации опоры и действующую на тело, называют силой реакции опоры (рис. 39).
, возникающую в результате деформации опоры и действующую на тело, называют силой реакции опоры (рис. 39).
 .
. .
. обозначен коэффициент пропорциональности, называемый коэффициентом трения.
обозначен коэффициент пропорциональности, называемый коэффициентом трения.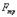 , как и модуль максимальной силы трения покоя, пропорционален модулю силы реакции опоры:
, как и модуль максимальной силы трения покоя, пропорционален модулю силы реакции опоры: .
.



