
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первый закон Ньютона – закон инерции. Инерциальная система отсчета.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. За первый закон движения Ньютон принял закон инерции, высказанный в частной форме еще Галилеем. Согласно этому закону тело, не подверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно. Такое тело называется свободным. Свободных тел не существует. Поэтому они являются физическими абстракциями. Однако можно поставить тело в такие условия, когда внешние воздействия на него по возможности устранены или практически компенсируют друг друга. Представив, что эти воздействия беспредельно уменьшаются, мы и приходим в пределе к представлению о свободном теле и свободном движении. 2. Закон инерции не может быть справедлив во всех системах отсчета. Классическая механика постулирует, что существует система отсчета, в которой все свободные тела движутся прямолинейно и равномерно. Такая система называется инерциальной системой отсчета. Таким образом, содержание закона инерции сводится к утверждению, что существует по крайней мере одна инерциальная система отсчета. 3. Земная система отсчета не может быть точно инерциальной, так как Земля испытывает два вращательных движения: вокруг собственной оси и вокруг Солнца. Однако эти движения происходят относительно медленно и для множества движений можно считать, что земная система отсчета инерциальна. Нужны специальные опыты, чтобы вскрыть ее инерциальность. Гелиоцентрическая система отсчета, оси в которой направлены на почти неподвижные удаленные звезды, еще лучше удовлетворяет требованию инерциальности. В этой системе можно изучать движение тел, малых по сравнению с размерами Галактики. 4. То есть, если существует класс движений, который мы желаем изучать, то всегда можно построить систему отсчета, которая будет инерциальной для данного класса движений. 6 Масса. Импульс. Второй закон Ньютона. Сила. 1. Всякое тело оказывает сопротивление при попытках привести его в движение или изменить модуль или направление его скорости. Это свойство называется инертностью. У разных тел оно проявляется в разной степени. Мера инертности называется массой. Для сравнения масс можно применить закон сохранения импульса, который будет сформулирован позднее. Из этого закона можно найти отношение масс. Для перехода от отношения масс к массам как таковым, необходимо выбрать эталон массы. 2. За эталон выбрана масса международного эталона килограмма, хранящегося в Международном бюро мер и весов (расположено в г. Севр близ Парижа) и представляющего собой цилиндр диаметром и высотой 39.17 мм из платино-иридиевого сплава (90 % платины, 10 % иридия). Первоначально килограмм определялся как масса одного кубического дециметра (литра) чистой воды при температуре 4 °C и стандартном атмосферном давлении на уровне моря. 3. Для формулировки второго закона Ньютона введем понятие импульса. Импульсом или количеством движения МТ называется вектор, равный произведению массы точки на ее скорость:
Импульсом или количеством движения системы материальных точек назовем сумму импульсов отдельных материальных точек:
Эти формулы годятся для медленных движений ( 4. Для формулировки второго закона Ньютона надо ввести понятие силы. Силой в механике считают всякую причину, изменяющую импульс тела. Это качественное определение. Количественное определение: в инерциальной системе отсчета производная импульса
Отсюда, второй закон Ньютона: в инерциальной системе отсчета производная импульса МТ по времени равна действующей на нее силе. Для медленных движений и постоянной массе эту формулу можно представить в виде:
Здесь Это уравнение не есть способ определения силы. Силы должны определятся как-нибудь по-другому. Например, с помощью динамометра. Подробности в учебнике. 3. Рассмотрим соотношение между первым и вторым законами Ньютона. Если положить 4. Второй закон Ньютона позволяет ввести единицу силы. В системе СИ такая единица называется ньютон (Н). Один ньютон = эта сила, которая массе в 1 кг сообщает ускорение в 1 м/с2.Есть другая система, очень любимая физиками, СГС (сантиметр (см), грамм (г), секунда (с)). В этой системе единица силы называется дина (дин).
7 Третий закон Ньютона. Формулирование задачи движения Рассмотрим замкнутую систему, состоящую из двух взаимодействующих МТ. В этом случае справедлив закон сохранения импульса
Дифференцируя это уравнение по времени и использовав второй закон Ньютона, получим:
Где Силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки. 2. Аналогично, можно сформулировать третий закон Ньютона, если МТ много. Для этого рассматриваются отдельно силы взаимодействия отдельных точек друг с другом. Пусть 3. Векторное уравнение движения МТ можно записать в координатной форме:
То есть получили три дифференциальных уравнения. Для их решения необходимо задать либо две векторные, либо шесть числовых постоянных. Обычно берут значения радиус-вектора Пример. Движение в поле силы тяжести. Галилеем было установлено, что все тела в пустоте вблизи Земли падают с одинаковым ускорением. Сила тяжести выражается формулой
Простым дифференцированием можно убедиться, что это уравнение имеет общее решение:
при произвольных значениях постоянных векторов 4. Для системы из
Силы в механике. Гравитационные силы. Закон всемирного тяготения. Принцип суперпозиции. Факты, подтверждающие закон всемирного тяготения. Сила упругости. Закон Гука. Сила трения. Сухое трение. Трение покоя. Трение скольжения. 1. Взаимодействие тел может происходить либо при непосредственном соприкосновении, либо на расстоянии. В первом случае взаимодействующие тела тянут или толкают друг друга. Возникающие при этом силы обычно вызываются деформациями тел. Если деформации малы, то от них можно отвлечься, учтя их влияние введением сил натяжения и давления. 2. Помимо сил, действующих при соприкосновении тел, в природе существуют силы, которые действуют на расстоянии, без участия промежуточной среды. К таким силам относятся гравитационные силы и силы взаимодействия наэлектризованных и намагниченных тел. 3. Согласно основным представлениям механики Ньютона силы, действующие на всякое тело в какой-либо момент времени, зависят от положения и скоростей остальных тел в тот же самый момент времени. Такое представление приводит к бесконечно большой скорости передачи взаимодействий. Опытные же факты привели к заключению, что скорость передачи взаимодействий ограничена скоростью света в вакууме. Отсюда сразу следует, что третий закон Ньютона не выполняется для взаимодействий на расстоянии. Физики нашли выход из этого. Они введи понятие поля. Тело 4. Сила упругости. Силами упругости называются силы, возникающие при деформации тел, то есть при изменении их формы и размеров. При этом изменяются расстояния между молекулами внутри тела, и электромагнитные силы пытаются вернуть молекулы обратно. Если после прекращения действия силы, вызвавшей деформацию, тело принимает первоначальную форму и размеры, то деформация называется упругой.
Простейшими деформациями являются деформации растяжения и сжатия. Они описываются законом Гука при малых упругих деформациях. На рисунке рассмотрен случай растяжения. Сила, вызывающая растяжения стержня обозначена
Здесь
Здесь
Аналогично представляется другая деформация — сдвига. Ее мы рассматривать не будем. Все малые деформации сводятся к деформациям растяжения и сдвига. 5. Гравитационная сила. Сила тяжести. Исаак Ньютон воспользовался тремя законами астронома Иоганна Кеплера и вывел закон всемирного тяготения, выражающийся формулой:
Здесь Вблизи планеты, в том числе вблизи Земли (
где Силы трения. Силы трения действует на поверхности между движущимися телами. Различают сухое трение между твердыми телами и внутреннее трение между отдельными слоями одной и той же жидкости.
В состоянии покоя вес и реакция опоры уравновешены. Если приложить силу Сила внутреннего трения будет рассмотрена в другом месте.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.60.132 (0.013 с.) |

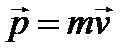 .
.
 ). В случае скоростей, близких к скорости света, формула для импульса МТ должна быть изменена.
). В случае скоростей, близких к скорости света, формула для импульса МТ должна быть изменена.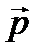 МТ по времени представляется уравнением:
МТ по времени представляется уравнением:

 однозначно определяется свойствами рассматриваемой МТ и окружающих ее тел, а также положениями и скоростями этих тел относительно МТ. Величина
однозначно определяется свойствами рассматриваемой МТ и окружающих ее тел, а также положениями и скоростями этих тел относительно МТ. Величина  называется слой, действующей на рассматриваемую МТ. В частных случаях сила может определяться только положением или только одной ее скоростью, но не может явно зависеть от ускорения этой точки. Из закона следует, что сила – вектор, и сложение сил подчиняется правилу параллелограмма.
называется слой, действующей на рассматриваемую МТ. В частных случаях сила может определяться только положением или только одной ее скоростью, но не может явно зависеть от ускорения этой точки. Из закона следует, что сила – вектор, и сложение сил подчиняется правилу параллелограмма. , то получится
, то получится  . Отсюда следует, что
. Отсюда следует, что  , т.е. импульс, а с ним и скорость свободно движущейся МТ постоянны. Таким образом, формально первый закон Ньютона следует из второго. Однако формула, определяющая второй закон Ньютона, имеет смысл только в инерциальных системах отсчета, а для введения таких систем требуется отдельный, первый закон Ньютона.
, т.е. импульс, а с ним и скорость свободно движущейся МТ постоянны. Таким образом, формально первый закон Ньютона следует из второго. Однако формула, определяющая второй закон Ньютона, имеет смысл только в инерциальных системах отсчета, а для введения таких систем требуется отдельный, первый закон Ньютона.
 материальных точек. Начальные условия.
материальных точек. Начальные условия.
 .
. и
и 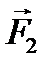 — силы, с которыми рассматриваемые МТ действуют друг на друга. Привлечем опытный факт, согласно которому силы
— силы, с которыми рассматриваемые МТ действуют друг на друга. Привлечем опытный факт, согласно которому силы 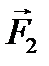 направлены вдоль прямой, соединяющей взаимодействующие точки. Тогда мы приходим к третьему закону Ньютона:
направлены вдоль прямой, соединяющей взаимодействующие точки. Тогда мы приходим к третьему закону Ньютона: — сила, с которой i -я точка действует на k -ю,
— сила, с которой i -я точка действует на k -ю,  — сила, с которой k -я точка действует на i -ю. Третий закон утверждает, что обе эти силы направлены вдоль прямой, соединяющей взаимодействующие точки, причем
— сила, с которой k -я точка действует на i -ю. Третий закон утверждает, что обе эти силы направлены вдоль прямой, соединяющей взаимодействующие точки, причем 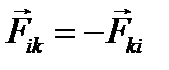 .
.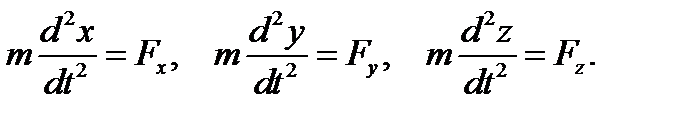
 и скорости
и скорости  в момент времени
в момент времени  . Их называют начальными условиями.
. Их называют начальными условиями. , и уравнение движения переходит в
, и уравнение движения переходит в .
.
 и
и  . Эти два вектора должны быть заданы при
. Эти два вектора должны быть заданы при  .
.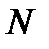 материальных точек необходимо задать начальный радиус-вектор и начальная скорость, т.е. всего
материальных точек необходимо задать начальный радиус-вектор и начальная скорость, т.е. всего 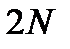 векторов или
векторов или  чисел, определяющих начальные значения координат и скоростей материальных точек системы.
чисел, определяющих начальные значения координат и скоростей материальных точек системы. возбуждают в окружающем пространстве силовое поле, которое в месте нахождения тела
возбуждают в окружающем пространстве силовое поле, которое в месте нахождения тела  проявляется в виде действующих на него сил. И обратно. Взаимодействия прикосновением являются частными случаями полевого взаимодействия — через молекулярные поля.
проявляется в виде действующих на него сил. И обратно. Взаимодействия прикосновением являются частными случаями полевого взаимодействия — через молекулярные поля.
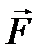 . Равная ей по величине и противоположно направленная возвращающая сила выражается через экспериментальный закон Гука:
. Равная ей по величине и противоположно направленная возвращающая сила выражается через экспериментальный закон Гука: .
. - размер, на который увеличилась длина стержня, а
- размер, на который увеличилась длина стержня, а  называется коэффициентом жесткости стержня. Знак минус указывает на то, что сила направлена в сторону, обратную изменения длины стержня. Если разделить силу на площадь сечения стержня
называется коэффициентом жесткости стержня. Знак минус указывает на то, что сила направлена в сторону, обратную изменения длины стержня. Если разделить силу на площадь сечения стержня  , а удлинение
, а удлинение  на первоначальную длину стержня
на первоначальную длину стержня  , то закон Гука преобразуется к виду:
, то закон Гука преобразуется к виду: .
. называется модулем Юнга и зависит только от вещества стержня. Для конкретного стержня величина
называется модулем Юнга и зависит только от вещества стержня. Для конкретного стержня величина  выражается из формулы
выражается из формулы .
. .
. и
и  — массы взаимодействующих материальных точек,
— массы взаимодействующих материальных точек,  — расстояние между точками,
— расстояние между точками, 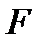 — сила взаимодействия,
— сила взаимодействия,  — гравитационная постоянная. Сила направлена по прямой, соединяющей МТ и является силой притяжения. В настоящее время этот закон обобщен в общей теории относительности. Как объясняется эта формула изнутри, пока не известно. За последние несколько лет выяснилось, что возможно существует темная материя, в которой предполагается гравитационная сила отталкивания.
— гравитационная постоянная. Сила направлена по прямой, соединяющей МТ и является силой притяжения. В настоящее время этот закон обобщен в общей теории относительности. Как объясняется эта формула изнутри, пока не известно. За последние несколько лет выяснилось, что возможно существует темная материя, в которой предполагается гравитационная сила отталкивания. ), эта формула преобразуется к виду:
), эта формула преобразуется к виду: ,
, называется ускорением свободного падения. Эта сила обычно называется силой тяжести.
называется ускорением свободного падения. Эта сила обычно называется силой тяжести. Сейчас рассмотрим сухое трение, которое в свою очередь подразделяется на трение скольжения и трение качение. Ограничимся трением скольжения, которое представлено на рисунке. Тело
Сейчас рассмотрим сухое трение, которое в свою очередь подразделяется на трение скольжения и трение качение. Ограничимся трением скольжения, которое представлено на рисунке. Тело  расположено поверх тела
расположено поверх тела  . Рассмотрим силы, действующие на тело
. Рассмотрим силы, действующие на тело  — вес тела,
— вес тела,  — сила реакции опоры,
— сила реакции опоры,  — сила, толкающая тело вправо,
— сила, толкающая тело вправо,  — сила трения скольжения.
— сила трения скольжения.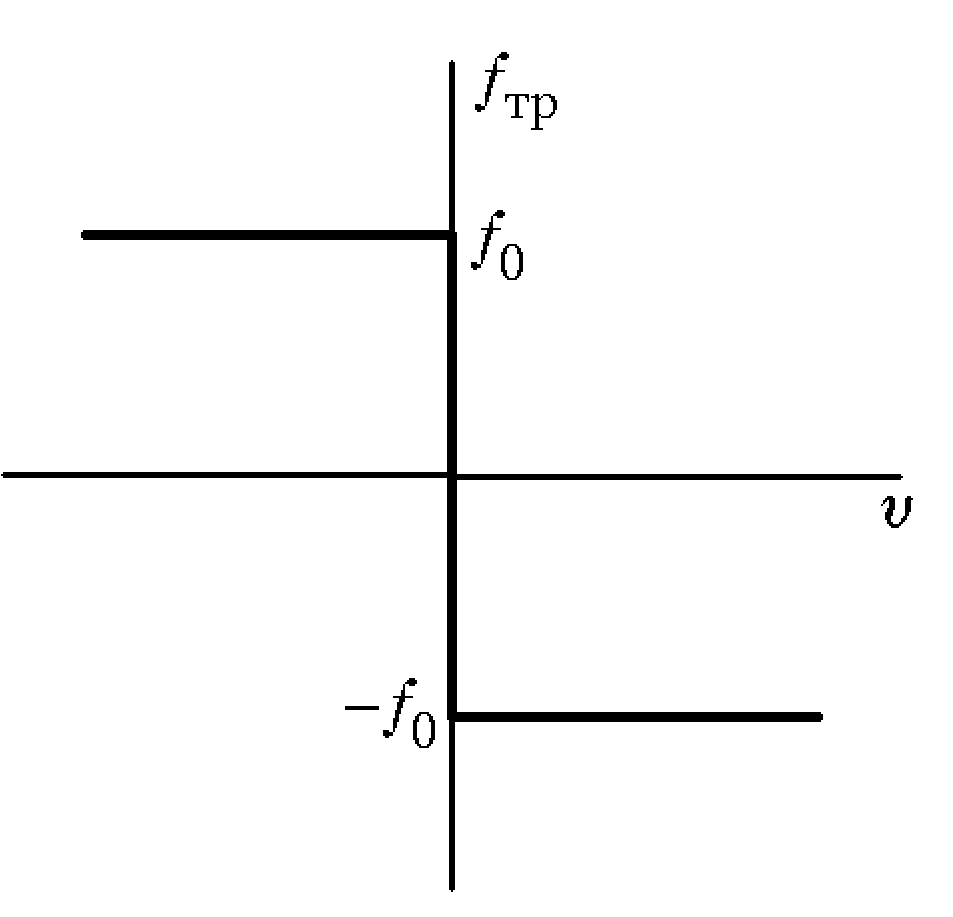
 . Для этой величины установлено, что
. Для этой величины установлено, что  , где
, где  — коэффициент трения. Определяется материалами тел. Приближенная зависимость силы трения от скорости движения верхнего тела относительно нижнего представлено на рисунке.
— коэффициент трения. Определяется материалами тел. Приближенная зависимость силы трения от скорости движения верхнего тела относительно нижнего представлено на рисунке.


