
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика материальной точки. Тело отсчета. Прямолинейное движение. Движение тела в пространстве. Декартова система координат. Система отсчета.Стр 1 из 10Следующая ⇒
Кинематика материальной точки. Тело отсчета. Прямолинейное движение. Движение тела в пространстве. Декартова система координат. Система отсчета. Тело отсчета — тело, относительно которого задается система отсчета. Простейшим объектом в механике является материальная точка – макроскопическое тело, размерами которого можно пренебречь при рассмотрении данного движения. Математически материальная точка эквивалентна математической точке, у которой есть одно физическое свойство – масса. Но тело должно оставаться макроскопическим. Иначе материальная точка может стать меньше молекулы. А движение молекул классической механикой не описывается. Если тело не может быть рассмотрено как материальная точка, то можно рассмотреть два случая. Более простой – когда расстояния между материальными точками, составляющими тело, не меняются во времени. Тогда тело называют абсолютно твердым телом, или просто твердым телом. Движения материальной точки и твердого тела могут быть рассмотрены в классической механике. Начнем с материальной точки (МТ). Описание движения МТ сводится к нахождению трех координат как функций времени: или к нахождению одной векторной функции Для того, чтобы сформулировать законы механики, необходимо ввести два новых понятия: понятие скорости и понятие ускорения. Прямолинейное движение
Рассмотрим частный случай, когда материальная точка движется по прямой линии. Примем эту прямую за координатную ось
Начнем уменьшать величину В математике такая величина называется производной функции
Скорость МТ является функцией времени Ускорение также является второй производной координаты по времени и обозначается
Декартова система координат В качестве пространственной системы отсчета можно взять произвольное твердое тело и связать с ним координатные оси, например, декартовой прямоугольной системы координат. Положение каждой точки в избранной системе отсчета можно задавать тремя числами:
где
Радиус-вектор, скорость и ускорение материальной точки, их связь с декартовыми координатами.
Перейдем к криволинейному движению МТ. Положение движущейся точки на траектории задается радиус-вектором
Силы в механике. Гравитационные силы. Закон всемирного тяготения. Принцип суперпозиции. Факты, подтверждающие закон всемирного тяготения. Сила упругости. Закон Гука. Сила трения. Сухое трение. Трение покоя. Трение скольжения. 1. Взаимодействие тел может происходить либо при непосредственном соприкосновении, либо на расстоянии. В первом случае взаимодействующие тела тянут или толкают друг друга. Возникающие при этом силы обычно вызываются деформациями тел. Если деформации малы, то от них можно отвлечься, учтя их влияние введением сил натяжения и давления. 2. Помимо сил, действующих при соприкосновении тел, в природе существуют силы, которые действуют на расстоянии, без участия промежуточной среды. К таким силам относятся гравитационные силы и силы взаимодействия наэлектризованных и намагниченных тел. 3. Согласно основным представлениям механики Ньютона силы, действующие на всякое тело в какой-либо момент времени, зависят от положения и скоростей остальных тел в тот же самый момент времени. Такое представление приводит к бесконечно большой скорости передачи взаимодействий. Опытные же факты привели к заключению, что скорость передачи взаимодействий ограничена скоростью света в вакууме. Отсюда сразу следует, что третий закон Ньютона не выполняется для взаимодействий на расстоянии. Физики нашли выход из этого. Они введи понятие поля. Тело
4. Сила упругости. Силами упругости называются силы, возникающие при деформации тел, то есть при изменении их формы и размеров. При этом изменяются расстояния между молекулами внутри тела, и электромагнитные силы пытаются вернуть молекулы обратно. Если после прекращения действия силы, вызвавшей деформацию, тело принимает первоначальную форму и размеры, то деформация называется упругой.
Простейшими деформациями являются деформации растяжения и сжатия. Они описываются законом Гука при малых упругих деформациях. На рисунке рассмотрен случай растяжения. Сила, вызывающая растяжения стержня обозначена
Здесь
Здесь
Аналогично представляется другая деформация — сдвига. Ее мы рассматривать не будем. Все малые деформации сводятся к деформациям растяжения и сдвига. 5. Гравитационная сила. Сила тяжести. Исаак Ньютон воспользовался тремя законами астронома Иоганна Кеплера и вывел закон всемирного тяготения, выражающийся формулой:
Здесь Вблизи планеты, в том числе вблизи Земли (
где Силы трения. Силы трения действует на поверхности между движущимися телами. Различают сухое трение между твердыми телами и внутреннее трение между отдельными слоями одной и той же жидкости.
В состоянии покоя вес и реакция опоры уравновешены. Если приложить силу
Сила внутреннего трения будет рассмотрена в другом месте.
Силы инерции Сила инерции — фиктивная сила, которую можно ввести в неинерциальной системе отсчёта так, чтобы законы механики в ней совпадали с законами инерциальных систем.
В математических вычислениях введения этой силы происходит путём преобразования уравнения
F1+F2+…Fn = ma к виду
F1+F2+…Fn–ma = 0 Где Fn — реально действующая сила, а –ma — «сила инерции».
Закон инерции про инерционные системы отсчёта гласит, что без влияния неуравновешенных сил тело будет сохранять свою скорость или неподвижность. В качестве примера силы инерции можно рассмотреть простую силу инерции, которую можно ввести в равноускоренной системе отсчёта: Пусть у нас есть быстро останавливающийся автобус. Все тела в нём будут нарушать закон инерции — они будут иметь тенденцию продолжать движение, и пассажирам придётся крепко держаться за поручни, чтобы не упасть вперёд, и оставаться неподвижными на своих местах относительно автобуса. Но если предположить, что всем пассажирам приходится противодействовать некой силе, то можно будет объяснить эту тенденцию её действием. Такую силу и назвали силой инерции. С введением этой силы закон инерции в автобусе восстановится — тела можно счесть подвергающимися действию этой силы, и тогда они будут вести себя в полном соответствии со вторым законом Ньютона. Т.е. если пассажиры приложат к себе относительно поручней дополнительную мускульную силу, противоположную силе инерции, то останутся на своих местах.
Среди сил инерции выделяют следующие: простую силу инерции, которую мы только что рассмотрели; центробежную силу, объясняющую стремление тел улететь от оси во вращающихся системах отсчёта; силу Кориолиса, объясняющую стремление тел сойти с радиуса при радиальном движении во вращающихся системах отсчёта; Закон сохранения импульса Импульсом системы МТ называется
Возьмем производную по времени от этого уравнения
Воспользуемся вторым законом Ньютона для каждой МТ, тогда справа будет сумма всех сил, действующих на все МТ. Внешние силы из-за замкнутости системы равны нулю, а сумма внутренних сил по третьему закону Ньютона также обращается в нуль. Следовательно,
сумма импульсов МТ в замкнутой системе остается постоянной во времени. Если равна нулю только проекция внешних сил на какое-то направление, то сохраняется только проекция полного импульса на это направление, например
Консервативные и неконсервативные силы. Потенциальная энергия. Примеры потенциальной энергии.
Все силы в физике подразделяются на консервативные и неконсервативные. Если силы взаимодействия зависят только от конфигурации МТ системы (т.е. их координат) и работа этих сил при перемещении системы из произвольного начального положения в произвольное конечное положение не зависит от пути перехода, а определяется только начальной и конечной конфигурациями системы, то такие силы называются консервативными.
Для консервативных сил выполняется следующее свойство. Рассмотрим перемещение МТ из точки 1 в точку 2 по двум путям: 123 и 142. Так как силы консервативные, то работы по этим двум траекториям равны: Все силы, не являющиеся консервативными, называются неконсервативными. Если на систему действуют только консервативные силы, то для такой системы можно ввести понятие потенциальной энергии. Примем какое-либо произвольное положение системы, характеризующееся заданием координат ее МТ, условно за нулевое. Работа, совершаемая консервативными силами при переходе системы из рассматриваемого положения в нулевое, называется потенциальной энергией системы в первом положении. Потенциальная энергия системы Нулевое положение произвольно. Поэтому потенциальная энергия меняется при изменении этого положения. Однако это не влияет на результаты вычислений. При изменении нулевого положения потенциальная энергия во всех точках поля сил меняется на одну и ту же постоянную, равную работе перехода из одной нулевой точки в другую. А в задаче всегда требуется работа при переходе из одной точки в другую, которая равна разности потенциальных энергий. То есть постоянная всегда вычитается и ответ не меняется. Формула для работы консервативных сил выражается формулой
то есть всегда из потенциальной энергии начальной точки вычитается потенциальная энергия конечной точки. Та же работа может быть выражена через кинетическую энергию. Приравнивая два выражения, получаем
Сумма кинетической и потенциальной энергий системы называется полной энергией системы
В системе с одними консервативными силами полная энергия системы остается неизменной. Это положение называется законом сохранения механической энергии. Приведем потенциальные энергии для некоторых сил. 1. Сила тяжести. 2. Потенциальна энергия растянутой пружины.
Если упругую энергию пружины в недеформированном состоянии считать равной нулю, то
3. Потенциальная энергия гравитационного притяжения двух МТ.
Если выбрать потенциальную энергию в бесконечности равной нулю, то
Потенциальная энергия отрицательна. Допустим теперь, что в системе кроме консервативных сил присутствуют неконсервативные, которые называются еще диссипативными. Тогда работа всех сил может быть разделена на две части: консервативную
или
То есть в этом случае полная механическая энергия уменьшается. Работа диссипативных сил переводит механическую энергию во внутреннюю тел, составляющих систему. На сегодняшний день считается, что если учесть все энергии, а не только механическую, то суммарная энергия сохраняется. Теорема Гюйгенса-Штейнера. Вычисление моментов инерции. Примеры.
Найдем связь между моментами инерции относительно двух параллельных осей. Предполагается, что эти оси перпендикулярны к плоскости рисунка и пересекают ее в точках
Интеграл слева есть момент инерции
Допустим, что ось
Это соотношение называется теоремой Гюйгенса-Штейнера. Вычислим моменты инерции некоторых тел.
а. Бесконечно тонкий однородный стержень длиной
а относительно оси проходящей через конец стержня равен
б. Бесконечно тонкое круглое кольцо (окружность). Момент инерции относительно оси
где
в. Бесконечно тонкий однородный диск и сплошной цилиндр. Момент инерции относительно оси, перпендикулярной основанию цилиндра (диску) через центр инерции равен
г. Момент инерции полого шара с бесконечно тонкими стенками относительно оси, проходящей через центр инерции, равен:
д. Момент инерции сплошного однородного шара с относительно оси, проходящей через центр инерции, равен:
Физический маятник. Физический маятник.
Физическим маятником называется твердое тело, которое может качаться вокруг неподвижной оси. Точка
где
где
Отсюда частота колебаний физического маятника равна
и период
Частным случаем физического маятника является математический маятник. Тогда
Уравнение идеального газа. Уравнение состояния заданной массы газа должно иметь вид
где Термодинамическая температура
Объем измеряется в м3. Идеальным газом называется газ, параметры которого подчиняется уравнению Клапейрона—Менделеева:
Здесь
Отношение
Если рассматривать смесь различных идеальных газов (например, воздух), то надо сформулировать закон Дальтона. Пусть несколько идеальных газов занимают один и тот же объем (молекулы перемешиваются). Для каждого газа можно ввести свое отдельное давление, которое будет в этом газе, если бы всех остальных не было в объеме. Оно называется парциальным и в соответствии с уравнением идеального газа равно
где Дальтон экспериментально установил, что полное давление смеси равно сумме парциальных давлений
Кроме выше данного определения, ничего не говорящего о свойствах молекул газа, можно ввести физическое определение идеального газа. Идеальным газом называется газ, молекулы которого не взаимодействуют на расстоянии и при столкновении ведут себя абсолютно упруго. А суммарный объем всех молекул данного газа пренебрежимо мал по сравнению с объемом газа.
Диффузия. Диффузией называется проникновение микрочастиц одного вещества в область пространства, занятого другим веществом. Диффузия может наблюдаться как в газах или жидкостях, так и в твердых веществах.
Если в смеси газов в одной области пространства концентрация молекул одного из них велика, а в другой, соседней области пространства мала, то будет наблюдаться проникновение молекул этого газа во вторую область, т.е. перенос массы молекул данного газа. Так движение молекулы хаотично, то скорость диффузионного проникновения из одной области в другую значительно меньше скорости их теплового движения. Рассмотрим случай, когда концентрация молекул каждого из газов в смеси зависит только от одной координаты
Здесь Если обе части уравнения умножить на массу молекулы газа, то это уравнение преобразуется к виду
где Если состояние смеси мало отличается от равновесного, то из статистической теории можно приближенно получить:
Теплопроводность. Теплопроводность — это передача энергии из одной части тела в другую. В случае газа можно рассмотреть одномерную задачу, как в диффузии. На рисунке надо заменить концентрацию на температуру
Здесь
Здесь В металлах теплопроводность обусловлена хаотическим движением электронов. Исследуется при помощи квантовой теории.
Различные типы магнетиков.
Все вещества являются магнетиками, т.е. подвержены влиянию магнитного поля. Они подразделяются, во-первых, на слабомагнитные, у которых Слабомагнитные вещества в свою очередь делятся на парамагнетики, у которых Сильномагнитные вещества не только обладают
Электромагнитная индукция Электромагнитная индукция была открыта Фарадеем в 1831 г. Для демонстрации этого явления возьмем неподвижный магнит и проволочную катушку, концы которой соединены с гальванометром. Если катушку приближать к одному из полюсов магнита, то во время движения стрелка гальванометра отклоняется — в катушке возбуждается электрический ток. При движении катушки в обратном направлении направление тока меняется на противоположное. Магнит можно заменить другой катушкой с током или электромагнитом. Этот ток называется индукционным током, а само явление — электромагнитной индукцией.
Возбуждение электрического тока при движении проводника в магнитном поле объясняется действием силы Лоренца, возникающей при движении проводника. Рассмотрим простейший случай, когда два параллельных провода Возникает напряженность стороннего поля, равная
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 519; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.119.241 (0.164 с.) |
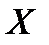 , поместив начало координат
, поместив начало координат  в произвольной ее точке. Положение МТ определяется одной координатой
в произвольной ее точке. Положение МТ определяется одной координатой  . Пусть в какой-то момент времени
. Пусть в какой-то момент времени  координата МТ равна
координата МТ равна  . В более поздний момент ее координата равна
. В более поздний момент ее координата равна 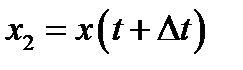 . За время
. За время 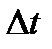 МТ испытывает перемещение
МТ испытывает перемещение  . Отношение
. Отношение  к
к  и
и  :
: 
 .
.  . Производная скорости по времени называется ускорением МТ. Ускорение обозначается через
. Производная скорости по времени называется ускорением МТ. Ускорение обозначается через 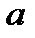 .
.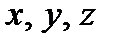 , представляющие собой расстояния от этой точки до координатных плоскостей
, представляющие собой расстояния от этой точки до координатных плоскостей  соответственно (рис. 1). Координаты можно объединить в радиус-вектор
соответственно (рис. 1). Координаты можно объединить в радиус-вектор  , проведенный из начала координат в рассматриваемую точку:
, проведенный из начала координат в рассматриваемую точку: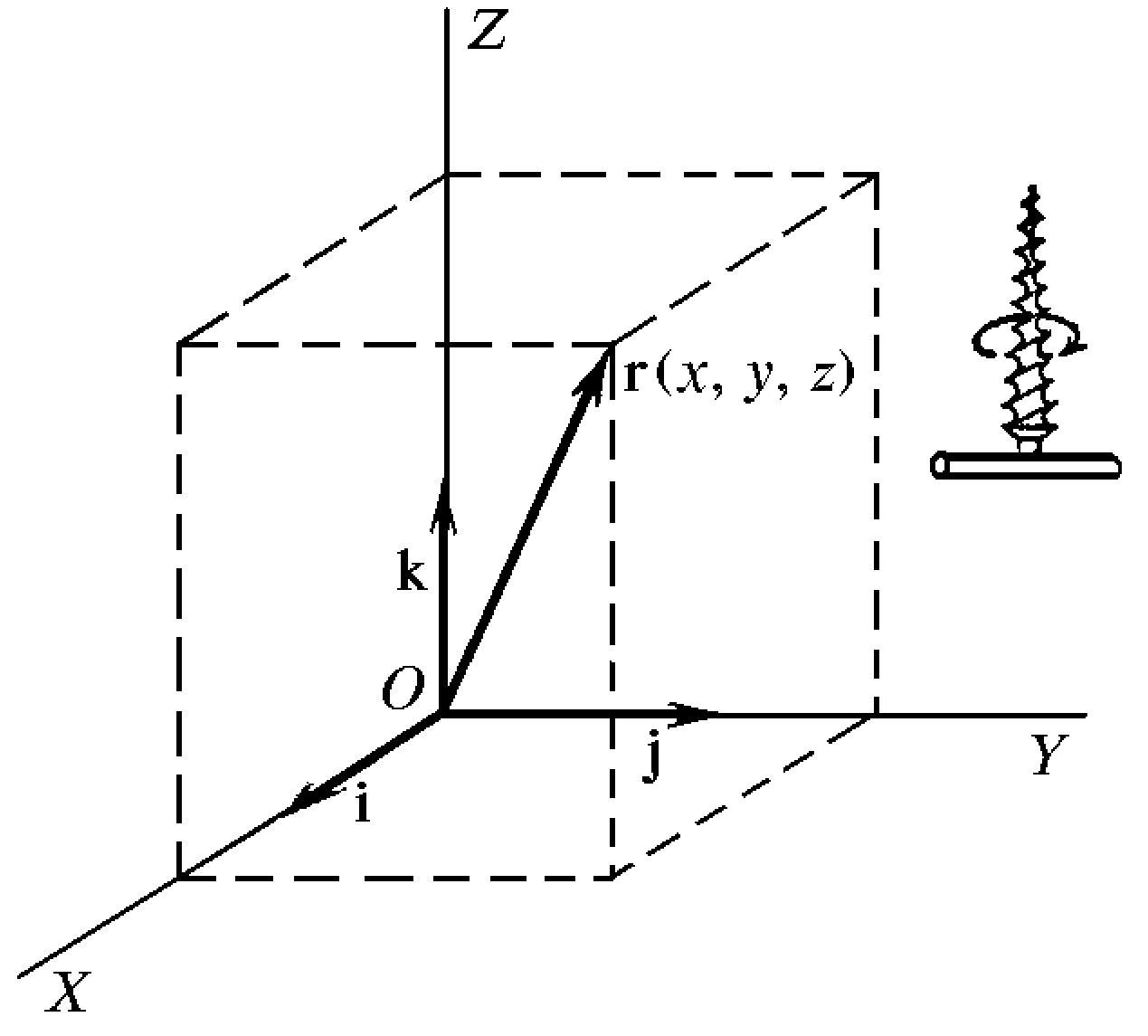

 — координатные орты, т.е. единичные векторы вдоль координатных осей
— координатные орты, т.е. единичные векторы вдоль координатных осей 
 , проведенным в эту точку из начала координат
, проведенным в эту точку из начала координат  . (остальное смотреть выше)
. (остальное смотреть выше) возбуждают в окружающем пространстве силовое поле, которое в месте нахождения тела
возбуждают в окружающем пространстве силовое поле, которое в месте нахождения тела  проявляется в виде действующих на него сил. И обратно. Взаимодействия прикосновением являются частными случаями полевого взаимодействия — через молекулярные поля.
проявляется в виде действующих на него сил. И обратно. Взаимодействия прикосновением являются частными случаями полевого взаимодействия — через молекулярные поля.
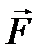 . Равная ей по величине и противоположно направленная возвращающая сила выражается через экспериментальный закон Гука:
. Равная ей по величине и противоположно направленная возвращающая сила выражается через экспериментальный закон Гука: .
. - размер, на который увеличилась длина стержня, а
- размер, на который увеличилась длина стержня, а  называется коэффициентом жесткости стержня. Знак минус указывает на то, что сила направлена в сторону, обратную изменения длины стержня. Если разделить силу на площадь сечения стержня
называется коэффициентом жесткости стержня. Знак минус указывает на то, что сила направлена в сторону, обратную изменения длины стержня. Если разделить силу на площадь сечения стержня  , а удлинение
, а удлинение  на первоначальную длину стержня
на первоначальную длину стержня  , то закон Гука преобразуется к виду:
, то закон Гука преобразуется к виду: .
. называется модулем Юнга и зависит только от вещества стержня. Для конкретного стержня величина
называется модулем Юнга и зависит только от вещества стержня. Для конкретного стержня величина  выражается из формулы
выражается из формулы .
. .
. и
и  — массы взаимодействующих материальных точек,
— массы взаимодействующих материальных точек,  — расстояние между точками,
— расстояние между точками, 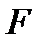 — сила взаимодействия,
— сила взаимодействия,  — гравитационная постоянная. Сила направлена по прямой, соединяющей МТ и является силой притяжения. В настоящее время этот закон обобщен в общей теории относительности. Как объясняется эта формула изнутри, пока не известно. За последние несколько лет выяснилось, что возможно существует темная материя, в которой предполагается гравитационная сила отталкивания.
— гравитационная постоянная. Сила направлена по прямой, соединяющей МТ и является силой притяжения. В настоящее время этот закон обобщен в общей теории относительности. Как объясняется эта формула изнутри, пока не известно. За последние несколько лет выяснилось, что возможно существует темная материя, в которой предполагается гравитационная сила отталкивания. ), эта формула преобразуется к виду:
), эта формула преобразуется к виду: ,
, называется ускорением свободного падения. Эта сила обычно называется силой тяжести.
называется ускорением свободного падения. Эта сила обычно называется силой тяжести. Сейчас рассмотрим сухое трение, которое в свою очередь подразделяется на трение скольжения и трение качение. Ограничимся трением скольжения, которое представлено на рисунке. Тело
Сейчас рассмотрим сухое трение, которое в свою очередь подразделяется на трение скольжения и трение качение. Ограничимся трением скольжения, которое представлено на рисунке. Тело  расположено поверх тела
расположено поверх тела  . Рассмотрим силы, действующие на тело
. Рассмотрим силы, действующие на тело  — вес тела,
— вес тела,  — сила реакции опоры,
— сила реакции опоры,  — сила, толкающая тело вправо,
— сила, толкающая тело вправо,  — сила трения скольжения.
— сила трения скольжения.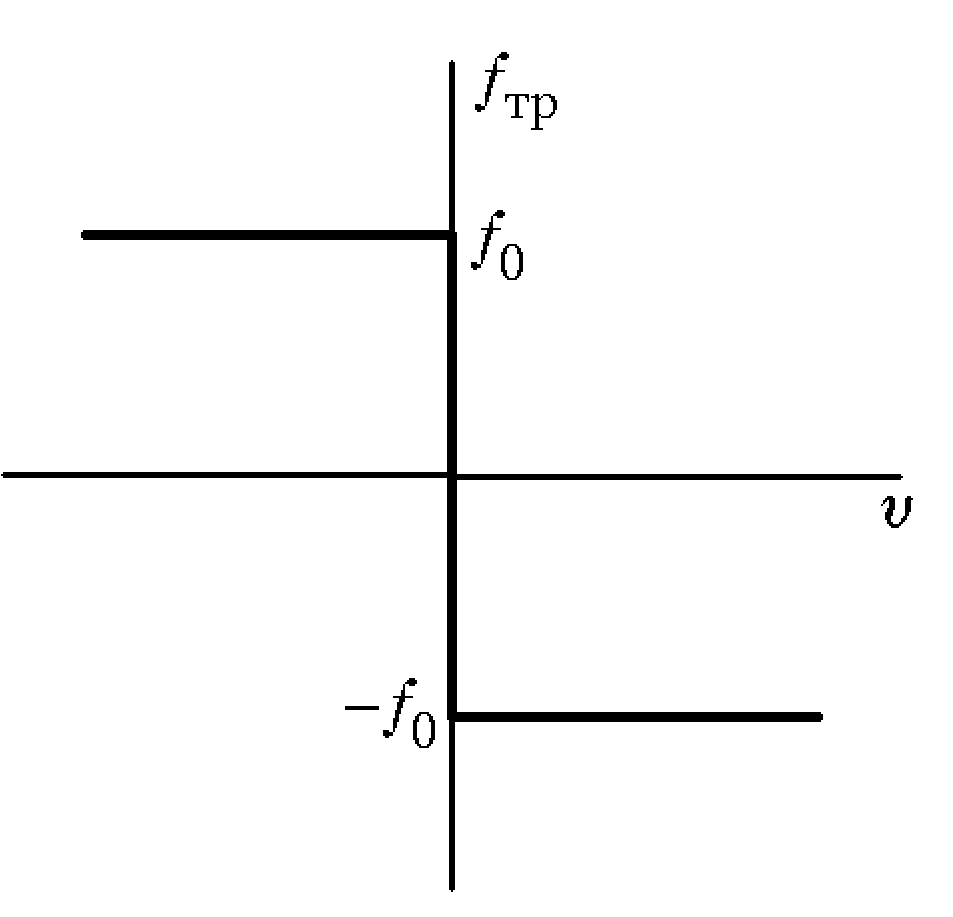
 . Для этой величины установлено, что
. Для этой величины установлено, что  , где
, где  — коэффициент трения. Определяется материалами тел. Приближенная зависимость силы трения от скорости движения верхнего тела относительно нижнего представлено на рисунке.
— коэффициент трения. Определяется материалами тел. Приближенная зависимость силы трения от скорости движения верхнего тела относительно нижнего представлено на рисунке. .
. .
. , и
, и
 .
.
 . Так кА силы зависят только от конфигурации, то
. Так кА силы зависят только от конфигурации, то  , где
, где 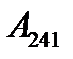 — работа, совершаемая при обратном движении по пути 241. Отсюда следует, что
— работа, совершаемая при обратном движении по пути 241. Отсюда следует, что  , то есть работа по замкнутому пути равна нулю. Свойство: работа консервативных сил по любому замкнутому пути равна нулю. К консервативным силам относятся гравитационная сила, сила тяжести, упругая сила, сила Кулона и многие другие.
, то есть работа по замкнутому пути равна нулю. Свойство: работа консервативных сил по любому замкнутому пути равна нулю. К консервативным силам относятся гравитационная сила, сила тяжести, упругая сила, сила Кулона и многие другие. является функцией только ее координат.
является функцией только ее координат. ,
, , откуда
, откуда .
. . Таким образом,
. Таким образом,  , или
, или .
.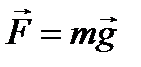 . Потенциальная энергия равна
. Потенциальная энергия равна  . Здесь
. Здесь  — высота положения МТ,
— высота положения МТ, 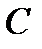 — произвольная константа. За нулевой уровень можно принять произвольный уровень, например уровень пола, уровень моря и т.д.
— произвольная константа. За нулевой уровень можно принять произвольный уровень, например уровень пола, уровень моря и т.д.  . Эта сила совершает работу
. Эта сила совершает работу .
. .
.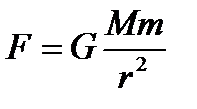 .
. .
. и диссипативную
и диссипативную  . Первая часть выражается через разность потенциальных энергий и вся работа выражается через разность кинетических энергий. Тогда
. Первая часть выражается через разность потенциальных энергий и вся работа выражается через разность кинетических энергий. Тогда ,
, .
.
 и
и  . Разобьем мысленно тело на элементарные массы
. Разобьем мысленно тело на элементарные массы  . Радиус-векторы одной из них, проведенные от осей
. Радиус-векторы одной из них, проведенные от осей 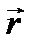 и
и  соответственно. Элементарная масса
соответственно. Элементарная масса  , где
, где  означает радиус-вектор
означает радиус-вектор  . Следовательно,
. Следовательно,  ,
,
 тела относительно оси
тела относительно оси  , первый интеграл справа — момент инерции
, первый интеграл справа — момент инерции 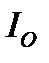 относительно оси
относительно оси  . Последний интеграл можно представить в виде
. Последний интеграл можно представить в виде  , где
, где 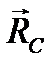 — радиус-вектор центра масс
— радиус-вектор центра масс  тела относительно оси
тела относительно оси  . Таким образом,
. Таким образом, .
. проходит через центр масс
проходит через центр масс 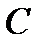 тела. Тогда
тела. Тогда  , и формула принимает вид
, и формула принимает вид .
.
 и массой
и массой 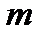 . Момент инерции относительно оси, проходящей через центр инерции перпендикулярно к стержню равен
. Момент инерции относительно оси, проходящей через центр инерции перпендикулярно к стержню равен ,
,
 .
. равен
равен ,
,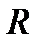 — радиус кольца.
— радиус кольца.
 .
.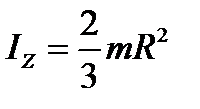 .
.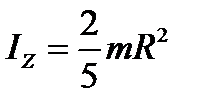 .
.
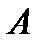 пересечения ее с вертикальной плоскостью, проходящей через центр масс маятника, называется точкой подвеса маятника. Положение тела в каждый момент времени можно характеризовать углом отклонения его из положения равновесия
пересечения ее с вертикальной плоскостью, проходящей через центр масс маятника, называется точкой подвеса маятника. Положение тела в каждый момент времени можно характеризовать углом отклонения его из положения равновесия  . Момент силы тяжести
. Момент силы тяжести  , приложенной к центру масс
, приложенной к центру масс 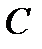 выражается формулой
выражается формулой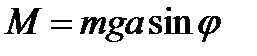 ,
, расстояние от центра масс до точки подвеса. Уравнение вращательного движения маятника выглядит так
расстояние от центра масс до точки подвеса. Уравнение вращательного движения маятника выглядит так ,
,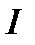 — момент инерции маятника относительно оси
— момент инерции маятника относительно оси  . Правая часть уравнения нелинейна относительна угла
. Правая часть уравнения нелинейна относительна угла 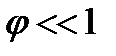 , то
, то  и мы получаем уравнение гармонического колебания величины
и мы получаем уравнение гармонического колебания величины 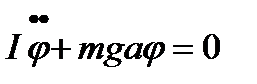 .
.
 .
. ,
,  , где
, где  — длина маятника и период равен
— длина маятника и период равен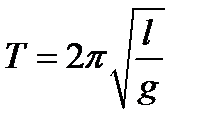 .
. ,
,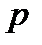 — давление,
— давление,  — объем,
— объем,  — термодинамическая температура. Единицей давления в СИ является паскаль (Па), равный Па=Н/м2. Внесистемной единицей давления является «миллиметр ртутного столба», причем 1 мм.рт.ст.=133,3 Па. Стандартное атмосферное давление на поверхности Земли составляет примерно 0,1 МПа.
— термодинамическая температура. Единицей давления в СИ является паскаль (Па), равный Па=Н/м2. Внесистемной единицей давления является «миллиметр ртутного столба», причем 1 мм.рт.ст.=133,3 Па. Стандартное атмосферное давление на поверхности Земли составляет примерно 0,1 МПа. , называемая также абсолютной, измеряется в кельвинах (К). Связь между ней и температурой
, называемая также абсолютной, измеряется в кельвинах (К). Связь между ней и температурой 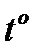 , единицей которой является градус Цельсия (
, единицей которой является градус Цельсия (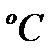 ), имеет вид
), имеет вид
 .
. — масса газа,
— масса газа, 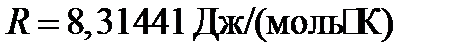 — универсальная газовая постоянная. Это уравнение может быть преобразовано к некоторым другим видам. Наиболее важный получится, если обе уравнения разделить на объем и представить отношение число молей
— универсальная газовая постоянная. Это уравнение может быть преобразовано к некоторым другим видам. Наиболее важный получится, если обе уравнения разделить на объем и представить отношение число молей 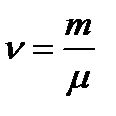 в виде
в виде  , где
, где  — число молекул в газе. Определим теперь концентрацию
— число молекул в газе. Определим теперь концентрацию  и уравнение преобразуется к виду
и уравнение преобразуется к виду .
.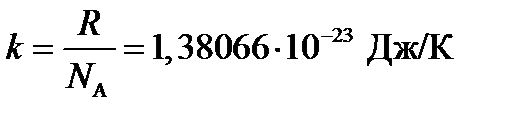 называется постоянной Больцмана. Уравнение состояния еще более упрощается
называется постоянной Больцмана. Уравнение состояния еще более упрощается .
. ,
, — номер газа.
— номер газа. .
.
 . Если мысленно выделить в пространстве некоторую площадку
. Если мысленно выделить в пространстве некоторую площадку  , ортогональную к оси
, ортогональную к оси  , то поток молекул газа через эту площадку (число молекул, проходящих в единицу времени), как показывает опыт, будет равен
, то поток молекул газа через эту площадку (число молекул, проходящих в единицу времени), как показывает опыт, будет равен .
. называется коэффициентом диффузии, а производная
называется коэффициентом диффузии, а производная  называется градиентом концентрации молекул газа. В трехмерном случае эта производная превращается в вектор градиента. Знак минус в формуле подчеркивает тот факт, что перенос молекул всегда происходит в направлении, противоположном направлению возрастания концентрации.
называется градиентом концентрации молекул газа. В трехмерном случае эта производная превращается в вектор градиента. Знак минус в формуле подчеркивает тот факт, что перенос молекул всегда происходит в направлении, противоположном направлению возрастания концентрации. ,
, переносимая в единицу времени масса, а
переносимая в единицу времени масса, а 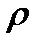 обозначает плотность газа в данном месте. В таком виде уравнение представляет собой закон Фика. Коэффициент диффузии
обозначает плотность газа в данном месте. В таком виде уравнение представляет собой закон Фика. Коэффициент диффузии  .
. и поток частиц на поток тепла
и поток частиц на поток тепла  . Тогда имеем для теплопроводности закон Фурье
. Тогда имеем для теплопроводности закон Фурье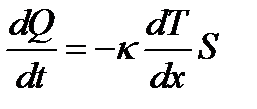 .
. (каппа) — коэффициент теплопроводности,
(каппа) — коэффициент теплопроводности,  — градиент температуры. Знак минус показывает, что тепло передается от более горячей области вещества к более холодной. В случае почти равновесия в газе
— градиент температуры. Знак минус показывает, что тепло передается от более горячей области вещества к более холодной. В случае почти равновесия в газе  .
. — плотность газа,
— плотность газа,  — удельная теплоемкость газа при постоянном объеме. В СИ коэффициент теплопроводности измеряется в
— удельная теплоемкость газа при постоянном объеме. В СИ коэффициент теплопроводности измеряется в 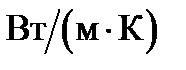 .
.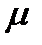 близок к единице и сильномагнитные, у которых он может быть очень большим.
близок к единице и сильномагнитные, у которых он может быть очень большим.
 и
и  помещены в постоянное однородное магнитное поле, перпендикулярное к плоскости рисунка и направленное на нас. (см. рис.) Слева провода
помещены в постоянное однородное магнитное поле, перпендикулярное к плоскости рисунка и направленное на нас. (см. рис.) Слева провода  . Когда мостик движется вправо со скоростью
. Когда мостик движется вправо со скоростью  , вместе с ним движутся электроны и положительные ионы. На каждый движущийся заряд
, вместе с ним движутся электроны и положительные ионы. На каждый движущийся заряд  в магнитном поле действует сила Лоренца
в магнитном поле действует сила Лоренца  . На положительный ион она действует вниз, на отрицательный электрон — вверх. Электроны начнут перемещаться вверх и там будет скапливаться отрицательный заряд, внизу останется больше положительных ионов. То есть положительные и отрицательные заряды разделяются, возникает электрическое поле вдоль мостика, и потечет ток. Этот ток называется индукционным. Ток потечет и в других частях контура
. На положительный ион она действует вниз, на отрицательный электрон — вверх. Электроны начнут перемещаться вверх и там будет скапливаться отрицательный заряд, внизу останется больше положительных ионов. То есть положительные и отрицательные заряды разделяются, возникает электрическое поле вдоль мостика, и потечет ток. Этот ток называется индукционным. Ток потечет и в других частях контура  . На рисунке токи изображены сплошными стрелками.
. На рисунке токи изображены сплошными стрелками. .Электродвижущая сила, создаваемая этим полем, называется электродвижущей силой индукции и обозначается
.Электродвижущая сила, создаваемая этим полем, называется электродвижущей силой индукции и обозначается  . В рассматриваемом случае
. В рассматриваемом случае  , где
, где  — длина мостика. Знак минус поставлен потому, что стороннее поле
— длина мостика. Знак минус поставлен потому, что стороннее поле 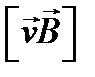 направлено против положительного обхода контура, определяемого вектором
направлено против положительного обхода контура, определяемого вектором  по правилу правого винта. Величина
по правилу правого винта. Величина  есть приращение площади контура
есть приращение площади контура  в единицу времени. Поэтому
в единицу времени. Поэтому  равна
равна  , т.е. скорости приращения магнитного потока, пронизывающего площадь контура
, т.е. скорости приращения магнитного потока, пронизывающего площадь контура  .
.


