
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неинерциальные системы отсчета. Силы инерции.Содержание книги
Поиск на нашем сайте Неинерциальной системой отсчета называется система, которая движется ускоренно относительно инерциальных систем. Законы Ньютона выполняются в инерциальных системах отсчета. Запишем второй закон Ньютона в виде
Смысл индекса «абс» выяснится в дальнейшем. Для нахождения уравнений движения в неинерциальных системах отсчета необходимо установить законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной системе отсчета. Ограничим рассмотрение малыми скоростями Условимся называть неподвижной произвольно выбранную инерциальную систему отсчета, а движение относительно нее — абсолютным. Именно только в этом смысле ускорение будет называться абсолютным. Абсолютное движение тела складывается из движения тела относительно рассматриваемой системы отсчета и движения системы отсчета относительно неподвижной системы отсчета. Первое называется относительным, второе – переносным. Нашей целью является получить уравнение движения относительно любой системы отсчета. В инерциальной системе таким уравнением является уравнение второго закона Ньютона.
Возьмем две системы отсчета: неподвижную систему
Дважды дифференцируя это уравнение по времени, получим
Рассмотрим простейший случай, когда система
Подставим теперь выражение для ускорения в закон Ньютона. Получим
Это и есть уравнение относительного движения МТ. Правая часть состоит из двух членов. Первый из них есть настоящая сила, которая не меняется при переходе из одной системы координат в другую, т.к. зависит от разности координат и разности скоростей действующих МТ. Второй член представляет из себя силу инерции, в этом случае поступательную. Эта сила меняется при переходе от одной неинерциальной системы отсчета к другой. Эта сила не подчиняется третьему закону Ньютона. Если считать, что все силы являются результатом взаимодействия тел, то силы инерции фиктивны. Допустим теперь, что система отсчета
При каждом дифференцировании радиус-вектора по времени появляется дополнительный член, связанный с указанным эффектом. При этом из определения скорости (и ускорения) в системе отсчета следует:
Члены, получаемые из вращения ортов, в случае скорости должны быть отнесены к переносным величинам:
С ускорением несколько сложнее:
Вектор
где Уравнение для относительного движения выглядит так:
или более подробно
Все члены, стоящие справа, кроме Действие силы Кориолиса траектория МТ не изменилась, необходимо настоящая сила, действующая в сторону вращения. Физически МТ переходит от малого радиуса (и линейной скорости) к большим. Но движение самой МТ вдоль направления вращения имеет ту же линейную скорость, что и при малом радиусе. Поэтому она должна отстать. На рисунке б показано движение к центру вращения.
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 .
. , т.е все скорости, в том числе и скорость системы отсчета, малы по сравнению со скоростью света в вакууме.
, т.е все скорости, в том числе и скорость системы отсчета, малы по сравнению со скоростью света в вакууме.
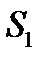 с началом координат в точке
с началом координат в точке  и движущуюся систему
и движущуюся систему  с началом координат в точке
с началом координат в точке  . Пусть
. Пусть 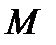 — какая-либо МТ. Все необходимые векторы введены на рисунке. Векторы
— какая-либо МТ. Все необходимые векторы введены на рисунке. Векторы  в каждый момент времени связаны соотношением
в каждый момент времени связаны соотношением

 и ускорение
и ускорение  начала координат
начала координат  ,
,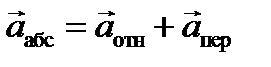
 .
.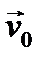 , равной скорости движения начала координат
, равной скорости движения начала координат  , и вращательное вокруг мгновенной оси, проходящей через это начало с угловой скоростью
, и вращательное вокруг мгновенной оси, проходящей через это начало с угловой скоростью  . Угловая скорость может меняться как по величине, так и по направлению. При вращении системы отсчета меняются не только проекции координат на оси вращающейся системы, а и направления единичных векторов в ней:
. Угловая скорость может меняться как по величине, так и по направлению. При вращении системы отсчета меняются не только проекции координат на оси вращающейся системы, а и направления единичных векторов в ней: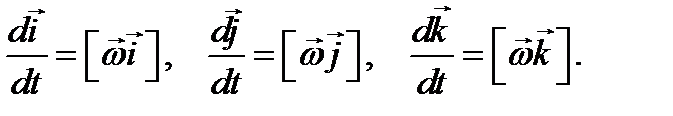



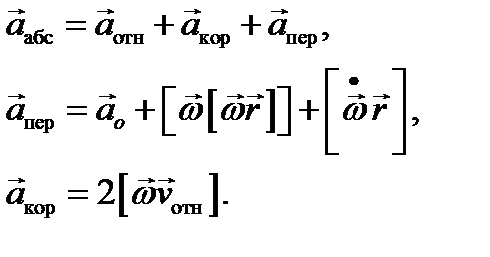
 зависит только от движения системы отсчета
зависит только от движения системы отсчета  относительно неподвижной системы
относительно неподвижной системы 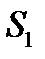 . Слагаемое
. Слагаемое  зависит как от относительного, так и от переносного движений. Оно называется кориолисовым ускорением. Второй член в переносном ускорении известен как центростремительное ускорение и может быть преобразован к виду
зависит как от относительного, так и от переносного движений. Оно называется кориолисовым ускорением. Второй член в переносном ускорении известен как центростремительное ускорение и может быть преобразован к виду ,
,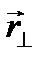 — проекция радиус-вектора, перпендикулярная оси вращения. Последний член связан с неравномерностью вращения системы отсчета.
— проекция радиус-вектора, перпендикулярная оси вращения. Последний член связан с неравномерностью вращения системы отсчета. ,
,
 , являются силами инерции.
, являются силами инерции. видно из рисунка. При удалении МТ точки от центра вращения на МТ действует сила Кориолиса, заставляющая ее двигаться против вращения системы отсчета (рис. а). И для того, чтобы
видно из рисунка. При удалении МТ точки от центра вращения на МТ действует сила Кориолиса, заставляющая ее двигаться против вращения системы отсчета (рис. а). И для того, чтобы 



