
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонические колебания. Основные характеристики колебательного процесса. Дифференциальное уравнение гармонических колебаний.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гармоническими колебаниями называется движение, происходящее по закону синуса (или косинуса):
где
Величина Выведем дифференциальное уравнение гармонических колебаний. Возьмем, например
и продифференцируем величину
Из последнего уравнения получаем
Это уравнение является дифференциальным уравнением гармонических колебаний. Его решением является ранее приведенные формулы для
Простейший пример гармонических колебаний получается при рассмотрении движения шарика, жестко связанного с невесомой пружиной. При этом считается, что трения нет. Пусть
Если положить
то есть в уравнение гармонических колебаний. Решение этого уравнения представимо в виде
и периодом
Период колебаний
Потенциальная и кинетическая энергии тела даются выражениями
Подставляем сюда зависимость
Учитывая формулу для частоты, получаем
То есть механическая энергия в этом случае сохраняется.
Пружинный маятник. Энергия маятника. Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.
Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.
В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене. Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:
Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:
В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:
Физический маятник. Физический маятник.
Физическим маятником называется твердое тело, которое может качаться вокруг неподвижной оси. Точка
где
где
Отсюда частота колебаний физического маятника равна
и период
Частным случаем физического маятника является математический маятник. Тогда
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.01 с.) |

 ,
, ,
, — мгновенное значение колеблющейся величины в момент времени
— мгновенное значение колеблющейся величины в момент времени 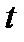 ,
,  — амплитуда колебаний, равная наибольшему значению
— амплитуда колебаний, равная наибольшему значению 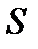 ,
, 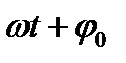 — фаза колебания, определяющая мгновенное значение колеблющейся величины,
— фаза колебания, определяющая мгновенное значение колеблющейся величины, 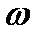 — круговая частота колебаний,
— круговая частота колебаний,  — начальная фаза колебаний. Время, в течение которого совершается одно полное колебание, называется периодом колебания
— начальная фаза колебаний. Время, в течение которого совершается одно полное колебание, называется периодом колебания 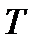 . Легко показать, что
. Легко показать, что .
. называется частотой колебания. Единица измерения частоты в СИ — 1 герц=1с-1. Выбор синуса или косинуса связан с удобством при рассмотрении конкретной задачи. Всегда можно изменить одну функцию на другую, изменив фазу на
называется частотой колебания. Единица измерения частоты в СИ — 1 герц=1с-1. Выбор синуса или косинуса связан с удобством при рассмотрении конкретной задачи. Всегда можно изменить одну функцию на другую, изменив фазу на 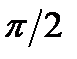 . Результат при этом не изменится.
. Результат при этом не изменится.
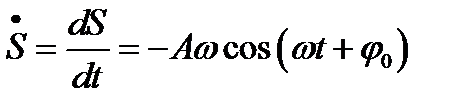 ,
,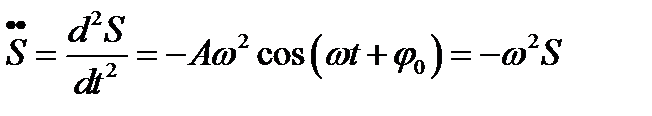 .
. .
. . При этом величины амплитуды и начальной фазы должны быть заданы отдельно.
. При этом величины амплитуды и начальной фазы должны быть заданы отдельно.
 — длина недеформированной пружины. Если пружину растянуть или сжать до длины
— длина недеформированной пружины. Если пружину растянуть или сжать до длины  , то возникает сила
, то возникает сила 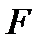 , стремящаяся вернуть тело в положение равновесия. При небольших растяжениях
, стремящаяся вернуть тело в положение равновесия. При небольших растяжениях 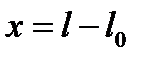 справедлив закон Гука
справедлив закон Гука 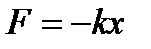 . Тогда уравнение движения тела имеет вид
. Тогда уравнение движения тела имеет вид .
. , то уравнение превратится в
, то уравнение превратится в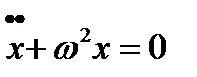 ,
,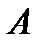 и
и  — любые. Отсюда также следует, что груз на пружине будет совершать гармонические колебания с круговой частотой
— любые. Отсюда также следует, что груз на пружине будет совершать гармонические колебания с круговой частотой
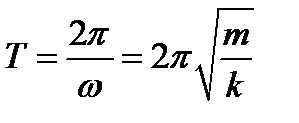 .
. не зависит от амплитуды
не зависит от амплитуды  . Это свойство, называемое изохронностью колебаний, выполняется, пока справедлив закон Гука. При больших растяжениях закон Гука не выполняется и появляется зависимость периода колебаний от амплитуды.
. Это свойство, называемое изохронностью колебаний, выполняется, пока справедлив закон Гука. При больших растяжениях закон Гука не выполняется и появляется зависимость периода колебаний от амплитуды.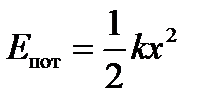 ,
, 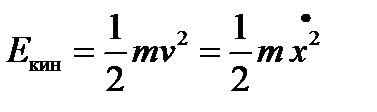 .
. от времени и получаем
от времени и получаем ,
, 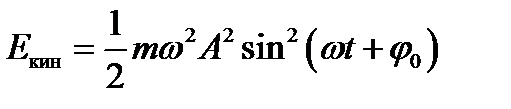 .
. .
.
 , где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.
, где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.

 пересечения ее с вертикальной плоскостью, проходящей через центр масс маятника, называется точкой подвеса маятника. Положение тела в каждый момент времени можно характеризовать углом отклонения его из положения равновесия
пересечения ее с вертикальной плоскостью, проходящей через центр масс маятника, называется точкой подвеса маятника. Положение тела в каждый момент времени можно характеризовать углом отклонения его из положения равновесия  . Момент силы тяжести
. Момент силы тяжести  , приложенной к центру масс
, приложенной к центру масс  выражается формулой
выражается формулой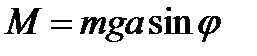 ,
, расстояние от центра масс до точки подвеса. Уравнение вращательного движения маятника выглядит так
расстояние от центра масс до точки подвеса. Уравнение вращательного движения маятника выглядит так ,
,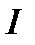 — момент инерции маятника относительно оси
— момент инерции маятника относительно оси  . Правая часть уравнения нелинейна относительна угла
. Правая часть уравнения нелинейна относительна угла 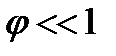 , то
, то  и мы получаем уравнение гармонического колебания величины
и мы получаем уравнение гармонического колебания величины 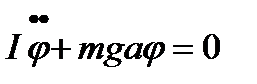 .
.
 .
. ,
,  , где
, где  — длина маятника и период равен
— длина маятника и период равен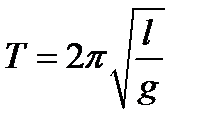 .
.


