
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонический анализ напряжения на выходе трёхфазного мостового выпрямителяСодержание книги
Поиск на нашем сайте
Пусть имеется трёхфазный мостовой выпрямитель, известный как схема Ларионова, с активной нагрузкой, подключенной к выходу (рис. 2.75).
VD 1 − VD 6
UA (t) ()
UB t UC (t)
Рис. 2.75
Необходимо проанализировать гармонический состав выходного напряжения выпрямителя с применением MathCAD. Зададим в MathCAD частоту и систему фазных напряжений стан-
Рис. 2.76
Модули фазных напряжений представлены на рис. 2.77.
Напряжение на выходе неуправляемого трёхфазного
мостового
Рис. 2.78
Зададим последовательность i, как порядковый номер гармоники
Рис. 2.79
Как видно из рис. 2.81
Рис. 2.80
Рис. 2.81
Представим исходную функцию гармоническим рядом с ограни- ченным числом гармоник (рис. 2.82) и оценим погрешность такого представления. Как видно, погрешность очень мала.
Рис. 2.83
Исходная функция выходного напряжения выпрямителя и соот-
Рис. 2.84
По графическому распределению коэффициентов гармоник вид- но, что ненулевыми являются шестая, двенадцатая, двадцать четвёртая гармоники (рис. 2.85). восемнадцатая и
Применение гребенчатой и прямоугольной функций для гармонического анализа в MathCAD
В предыдущем параграфе рассмотрен гармонический анализ на- пряжения на выходе неуправляемого выпрямителя. В случае гармони- ческого анализа выходных напряжений управляемых выпрямителей, ре- гуляторов переменного тока и инверторов для математического описа- ния исследуемых функций необходимо применять моугольные функции. Зададим в MathCAD период гребенчатые и пря- гребенчатой (пило- образной) функции в единицах СИ для наиболее распространённой час-
Рис. 2.86
Зададим в MathCAD гребенчатую функцию и построим её график (рис. 2.87).
Рис. 2.88
Зададим в MathCAD α=90, объявим прямоугольную функцию за- держки fα(t) и построим её график (рис. 2.89).
1 C1
I1 C2
R3 U2
Рис. 2.89
ГЛАВА 12. ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕ- НИЙ В MATHCAD
Пусть необходимо рассчитать переходные процессы I1(t), I2(t), U1(t), U2(t) при подключении нагруженного двухзвенного Г-образного LC – фильтра к источнику постоянного тока (рис. 2.90). На первом этапе выводится система из четырёх дифференциальных уравнений (рис. 2.91).
На втором этапе вводим параметры фильтра и функции правых частей дифференциальных уравнений (рис. 2.92).
Шаг расчёта рекомендуется брать пропорциональным среднегео- метрической величине от всех постоянных времени фильтра (рис. 2.93).
Решение методом Эйлера системы дифференциальных уравнений, описывающих состояние фильтра, с нулевыми начальными условиями показано на рис. 2.94. Здесь же показаны полученные графики переход-
Рис. 2.94
Процедура расчёта переходных процессов в MathCAD простей- шим методом (Эйлера) сводится к следующим этапам: – вывод системы дифференциальных уравнений, описывающих устройство; – ввод параметров устройства; – ввод функций правых частей дифференциальных уравнений; – расчёт или задание шага интегрирования; – ввод начальных условий; – запись расчётной процедуры; – построение графиков.
ГЛАВА 13.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.119.139 (0.01 с.) |

 Uвыпр (t) R н
Uвыпр (t) R н дартной промышленной трёхфазной сети (рис. 2.76).
дартной промышленной трёхфазной сети (рис. 2.76). Рис. 2.77
Рис. 2.77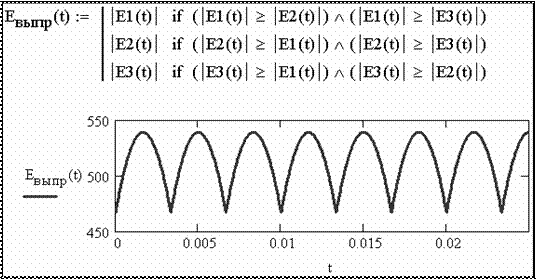 выпрямителя зададим функцией (рис. 2.78). Как видно из рис. 2.78, вы- ходное напряжение выпрямителя имеет значительную постоянную со- ставляющую и незначительные по амплитуде пульсации.
выпрямителя зададим функцией (рис. 2.78). Как видно из рис. 2.78, вы- ходное напряжение выпрямителя имеет значительную постоянную со- ставляющую и незначительные по амплитуде пульсации. (рис. 2.79). Рассчитаем коэффициенты гармоник (рис. 2.80).
(рис. 2.79). Рассчитаем коэффициенты гармоник (рис. 2.80). равны нулю.
равны нулю. в разложении синусные составляющие
в разложении синусные составляющие
 Рис. 2.82
Рис. 2.82 ветствующий конечный гармонический ряд практически совпадают во всех точках, кроме минимумов (рис. 2.84).
ветствующий конечный гармонический ряд практически совпадают во всех точках, кроме минимумов (рис. 2.84). Рис. 2.85
Рис. 2.85 тоты 50 Гц (рис. 2.86).
тоты 50 Гц (рис. 2.86). Рис. 2.87
Рис. 2.87 Во многих электротехнических устройствах и преобразователях выходное напряжение регулируется скважностью или продолжительно- стью открытого состояния γ. В управляемых выпрямителях и регулято- рах переменного тока выходное напряжение регулируется углом за- держки α (град.). Зададим в MathCAD γ=0.75, объявим прямоугольную функцию скважности f γ(t) и построим её график (рис. 2.88).
Во многих электротехнических устройствах и преобразователях выходное напряжение регулируется скважностью или продолжительно- стью открытого состояния γ. В управляемых выпрямителях и регулято- рах переменного тока выходное напряжение регулируется углом за- держки α (град.). Зададим в MathCAD γ=0.75, объявим прямоугольную функцию скважности f γ(t) и построим её график (рис. 2.88).
 3
3 Рис. 2.90. Двухзвенный Г-образный LC– фильтр.
Рис. 2.90. Двухзвенный Г-образный LC– фильтр. Рис. 2.91
Рис. 2.91 Рис. 2.92
Рис. 2.92 Рис. 2.93
Рис. 2.93 ных процессов.
ных процессов.


