
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение и анализ частотных характеристик вСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
MATHCAD
Рассмотрим задачу получения и анализа частотных характеристик однозвенного нагруженного Г-образного LC -фильтра низких частот (рис. 2.52) с применением MathCAD. В главе 8 выведено выражение (2.15) для операторной передаточ- ной функции ФНЧ. Пусть ω – частота входного сигнала (напряжения) ФНЧ, а j – мнимая единица. Заменим в (2.15) оператор Лапласа s на комплексную переменную j·ω
W (j ⋅ω) =
. 1 ⎞ +1 (2.19)
⎝ RНАГР ⎠ Преобразуем знаменатель выражения (2.19), выделив действи- тельную и мнимую части
W (j ⋅ω) =
1 − L ⋅ C ⋅ω2 + 1.
(2.20)
RНАГР ⎝ RНАГР ⎠
j ⋅ b = a − j ⋅ b = a − j ⋅ b . (2.21) a + Приняв j ⋅ b a − j ⋅ b a 2 + b 2 a 2 + b 2 a 2 + b 2
R RНАГР (2.22) и b = ω ⋅⎛ R ⋅ C +
L ⎞ (2.23) ,
⎝ RНАГР ⎠ и, учитывая (2.20) можно записать выражение для комплексной частот- ной характеристики ФНЧ
1 − L ⋅ C ⋅ ω 2 + R
(2.24) W (j ⋅ω) = 2 2 − ⎛ 1 − L ⋅ C ⋅ω2 + R ⎞ + ω2 ⋅⎛ R ⋅ C + L ⎞
⎝ RНАГР ⎠ ⎝ RНАГР ⎠
ω⋅⎛ R ⋅ C + L ⎞
⎛ 1 − L ⋅ C ⋅ω2 + R ⎞ + ω2 ⋅⎛ R ⋅ C + L ⎞
где ⎝
= P (ω)+ RНАГР ⎠ ⎝ j ⋅ Q (ω) = A (ω)⋅ e j ⋅ϕ(ω), RНАГР ⎠
P (ω) =
1 − L ⋅ C ⋅ ω 2 + R
(2.25)
– 2 2 ⎛ 1− L ⋅ C ⋅ω2 + R ⎞ + ω2 ⋅⎛ R ⋅ C + L ⎞
⎝ RНАГР ⎠ ⎝ RНАГР ⎠ – вещественно-частотная характеристика (ВЧХ) ФНЧ, ω⋅⎛ R ⋅ C + L ⎞ (2.26)
⎝ RНАГР ⎠ Q (ω)=− ⎛ 1 − L ⋅ C ⋅ω2 + 2 2 – R ⎞ +ω2 ⋅⎛ R ⋅ C + L ⎞
⎝ RНАГР ⎠ ⎝ RНАГР ⎠
P (ω)2 + Q (ω)2 – (2.27) – амплитудно-частотная характеристика (АЧХ) ФНЧ,
P (ω)
– фазо-частотная характеристика (ФЧХ) ФНЧ.
(2.28) Вектор (2.24) на комплексной плоскости частотных характеристик можно описать либо с помощью пары P (ω) и Q (ω), либо с помощью
A (ω)
и ϕ(ω). Наибольший интерес с практической точки зрения пред- ставляют A (ω) и ϕ(ω). Введём исходные данные в MathCAD(рис. 2.64).
Введём функции (2.25-2.28) в MathCAD(рис. 2.65).
Рис. 2.66
Приравняем производную к нулю и решим нелинейное уравнение с помощью процедуры solve (рис. 2.67).
Отбросим первый и третий полученные корни, а второй корень представим в виде функции, затем определим резонансные частоты при трёх значениях сопротивления нагрузки (рис. 2.68).
Амплитудно-частотные характеристики ФНЧ при разных сопро- тивлениях нагрузки представлены на рис. 2.69.
Рис. 2.69 Резонансная частота ФНЧ нелинейно зависит от сопротивления нагрузки (рис. 2.70).
Фазо-частотные характеристики ФНЧ при разных сопротивлениях нагрузки представлены на рис. 2.71.
Если повышать частоту входного сигнала ФНЧ начиная от резо-
снизится в 2 раз по сравнению с амплитудой при частоте, стремящей- ся к нулю. Такая частота определяет полосу пропускания ФНЧ. Опреде- лим полосу пропускания ФНЧ при ненагруженном режиме, решив не- линейное уравнение с помощью процедур solve. Результат представим в формате float (с плавающей точкой), взяв первые 6 значащих цифр ре- зультата (рис. 2.72).
Истинным решением будет первый корень, так как он является действительным положительным числом. Найдём полосы пропускания ФНЧ при втором и третьем сопро- тивлениях нагрузки (рис. 2.73).
Аналогично истинным решением будет в обоих случаях первый корень, так как он является действительным положительным числом. Численные результаты расчётов в ной главе внесём в табл. 2.2.
MathCAD, полученные в дан- Таблица 2.2
Как видно из табл. 2.2 резонансная частота и полоса пропускания ФНЧ при увеличении загруженности фильтра смещаются в сторону низких частот.
ГЛАВА 11. РАЗЛОЖЕНИЕ В РЯД ФУРЬЕ И АНАЛИЗ СИГНАЛОВ В MATHCAD
Как известно из курсов высшей математики и ТОЭ, любую пе- риодическую функцию можно разложить на гармонические составляю- щие – это составляет задачу гармонического или спектрального анализа. Обратная задача – задача гармонического синтеза состоит в генерации сигналов заданной формы методом суперпозиции гармонических сигна- лов разной амплитуды, фазы и частоты. MathCAD позволяет решать за- дачи гармонических анализа и синтеза с использованием встроенных процедур (рис. 2.74), либо непосредственно с помощью классических математических выражений.
Гармонический анализ сигналов находит применение в электро- технике, энергетике, электромеханике, электроприводе, системах управления. Обозначим исследуемый сигнал – периодическую функцию, ко- торую необходимо проанализировать, как f(t). Заменим функцию f(t) на конечную сумму Sn(t) по следующей формуле
a Sn (t) = 0 + a
cosω t + a
cos 2ω t +… + a
cos n ω t +
2 1 2 n (2.29) + b sin ω t + b sin 2ω t +… + b sin n ω t,
где 1 2 n a – постоянная составляющая, a,..., a – коэффициенты синусных составляющих, 1 n b,..., b – коэффициенты косинусных составляющих, 1 n ω –частота основной гармоники, n – количество членов разложения или количество гармоник. Средняя квадратичная ошибка, возникающая из-за конечного ко- личества гармоник, определим как
T δ2 =
⎡ f (t)− S
(t)⎤2 dt. ∫ ⎣ n ⎦ (2.30) где T – период повторяемости функции f(t). Коэффициент при косинусных составляющих разложения опреде- лим как 2 T
f (t)cos k ω tdt.
(2.31) Коэффициент при синусных составляющих разложения опреде- лим как 2 T
f (t)sin k ω tdt.
(2.32)
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.71.13 (0.01 с.) |

 (L ⋅ j ⋅ω+ R)⋅⎛ C ⋅ j ⋅ω+
(L ⋅ j ⋅ω+ R)⋅⎛ C ⋅ j ⋅ω+ ⎜ ⎟
⎜ ⎟ R + j ⋅ω⋅⎛ R ⋅ C + L ⎞
R + j ⋅ω⋅⎛ R ⋅ C + L ⎞



 1 ⋅ a −
1 ⋅ a − a = 1 − L ⋅ C ⋅ ω 2 +
a = 1 − L ⋅ C ⋅ ω 2 + ⎜ ⎟
⎜ ⎟
 RНАГР
RНАГР


 RНАГР
RНАГР ⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜ ⎟ – мнимо-частотная характеристика (МЧХ) ФНЧ,
– мнимо-частотная характеристика (МЧХ) ФНЧ,
 A (ω) = W (j ⋅ω) =
A (ω) = W (j ⋅ω) = ϕ(ω) = arg W (j ⋅ω) = arctgQ (ω) –
ϕ(ω) = arg W (j ⋅ω) = arctgQ (ω) –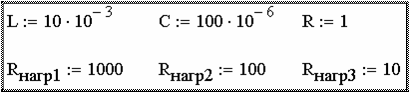 Рис. 2.64
Рис. 2.64 Рис. 2.65
Рис. 2.65 Для нахождения резонансной частоты ФНЧ необходимо АЧХ продифференцировать по частоте ω и ввести результат соответствую- щую функцию (рис. 2.66).
Для нахождения резонансной частоты ФНЧ необходимо АЧХ продифференцировать по частоте ω и ввести результат соответствую- щую функцию (рис. 2.66). Рис. 2.67
Рис. 2.67 Рис. 2.68
Рис. 2.68

 Рис. 2.70
Рис. 2.70 Рис. 2.71
Рис. 2.71 нансной, то амплитуда выходного напряжения при некоторой частоте
нансной, то амплитуда выходного напряжения при некоторой частоте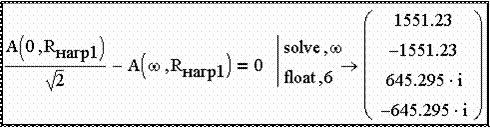 Рис. 2.72
Рис. 2.72 Рис. 2.73
Рис. 2.73 Рис. 2.74
Рис. 2.74 ak = T ∫
ak = T ∫ bk = T ∫
bk = T ∫


