
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы линейных алгебраических уравненийСодержание книги
Поиск на нашем сайте
Многие задачи на расчёт линейных электрических цепей постоян- ного и переменного тока легко и быстро решаются с применением MathCAD, однако пользователь должен уметь грамотно и безошибочно составлять системы линейных алгебраических уравнений (СЛАУ). Па- кет MathCAD позволяет решать системы линейных алгебраических уравнений практически неограниченной размерности всеми известными в настоящее время способами. Запишем систему n линейных алгебраических уравнений с n неиз- вестными a 11 ⋅ x 1 + a 12 ⋅ x 2 +...+ a 1 n ⋅ xn = b 1, a 21 ⋅ x 1 + a 22 ⋅ x 2 +...+ a 2 n ⋅ xn = b 2, ................................................. an 1 ⋅ x 1 + an 2 ⋅ x 2 +...+ ann ⋅ xn = bn. Совокупность коэффициентов этой системы запишем в виде матри- цы коэффициентов: ⎡ a 11 a 12 ... a 1 n ⎤ ⎢ ⎥ A = ⎢ a 21 a 22 ... a 2 n ⎥ ⎢..........................⎥ ⎢ ⎥ ⎢⎣ an 1 an 2 ... ann ⎥⎦ Система уравнений с учётом матрицы Aзапишется в виде A ⋅ X = B, где X и B – вектор-столбец неизвестных и вектор-столбец правых частей соответственно: ⎡ x 1 ⎤ ⎢ ⎥ ⎡ b ⎤ X = ⎢ x 2 ⎥, B = ⎢ b 2⎥. ⎢... ⎥ ⎢ ⎥ ⎢⎣ xn ⎥⎦ ⎢... ⎥ ⎢ ⎥ ⎢⎣ bn ⎥⎦ Методы решения СЛАУ делятся на прямые и итерационные. Прямые методы используют конечные соотношения (формулы) для вычисления неизвестных. К прямым методам решения СЛАУ относятся метод Гаус- са, метод обратной матрицы, метод Крамера. Прямые методы исполь- зуют обычно для сравнительно небольших систем (n < 200) с плотно за- полненной матрицей и не близким к нулю определителем. Итерацион- ные методы — это методы последовательных приближений. В них не- обходимо задать некоторое приближенное решение — начальное при- ближение. После этого с помощью некоторого алгоритма проводится один цикл вычислений, называемый итерацией. В результате итерации находят новое приближение. Итерации проводятся до получения реше- ния с требуемой точностью. К итерационным методам относятся метод простых итераций, метод Якоби, метод Зейделя. Подробно с методами решения СЛАУ можно ознакомиться в литературе [1, с. 114-154], [2, с. 216-226], [3, с. 126-155], [4, с. 24-93], [5, с. 41-65], [6, с. 133-145], [7, с. 21-36, 184-220], а также в [8, с. 7-21].
Расчёт цепи постоянного тока методами обратной матрицы и Кра- Мера
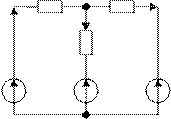
Пусть дана электрическая цепь (рис. 2.30), состоящая из трёх вет- вей. Известны величины ЭДС источников и сопротивлений в каждой ветви. Необходимо определить токи, протекающие в каждой ветви.
I1 I2 R2
E1 E2 E3
Рис. 2.30. Линейная электрическая цепь
Для трёх неизвестных токов I1, I2, I3 составим систему из трёх уравнений согласно первому и второму законам Кирхгофа
⎨ E 1 = I 1 ⋅ R 1 + I 3 ⋅ R 3 + E 3
и преобразуем её следующим образом
⎨ I 1 ⋅ R 1 + I 2 ⋅0 + I 3 ⋅ R 3 = E 1 − E 3. ⎪ I ⋅1− I ⋅1− I ⋅1 = 0 ⎩ 1 2 3
Рис. 2.31 На первом этапе задаём в единицах СИ величину параметров электрической цепи - сопротивление R (Ом), ЭДС источников E (В). На втором и третьем этапах формируем матрицы коэффициентов и свободных членов. Искомое решение на четвёртом этапе легко полу- чить методом обратной матрицы. Здесь Mr-1 – обратная матрица от мат- рицы коэффициентов, Mi– матрица токов (матрица решений СЛАУ). Следовательно величины искомых токов составят соответственно I1=1.6⋅10-3 А, I2=1⋅10-3 А, I3=6⋅10-3 А. Проведём проверку найденных решений, используя первое урав- нение СЛАУ Mi ⋅ R 1+ Mi ⋅ R 2+ E 2 = 20. 0 1 Проверка показывает правильность найденных решений. Данная СЛАУ несложно решается в пакете MathCAD и методом Крамера. Для решения СЛАУ методом Крамера введём три дополнитель- ных матрицы, получаемых заменой соответствующего столбца в матри- це коэффициентов на вектор-столбец правых частей (рис. 2.32).
Решение системы методом Крамера J1, J2, J3 определяется как от- ношение соответствующих частных определителей (от матриц M1, M2, M3) к полному определителю (от матрицы MR) (рис. 2.33).
Как видим решения J1, J2, J3, полученные методом Крамера совпа- дают с решениями, полученными методом обратной матрицы. Для студентов, желающих самостоятельно решить вышеприве- дённую систему в пакете MathCAD методами Гаусса, Якоби и Зейделя, рекомендуем обратиться к [8, с. 16-18]. СЛАУ, описывающая цепь переменного тока, решается аналогич- но, ответ получается в комплексном виде.
ГЛАВА 7. ГРАФИЧЕСКОЕ И ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Системы нелинейных уравнений важны при решении многих за- дач электротехники. Существует графический и численные способы решения систем нелинейных уравнений. Рассмотрим пример решения типовой задачи.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 538; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |

 3
3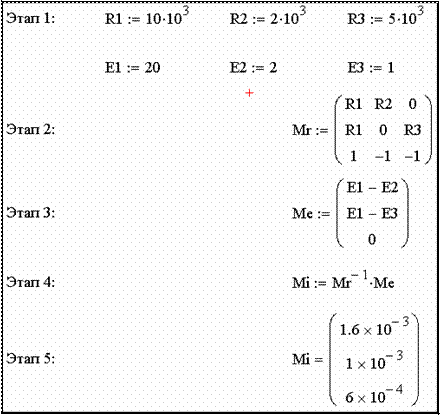 Решение задачи по этапам в MathCADприведено на рис. 2.31.
Решение задачи по этапам в MathCADприведено на рис. 2.31. Рис. 2.32
Рис. 2.32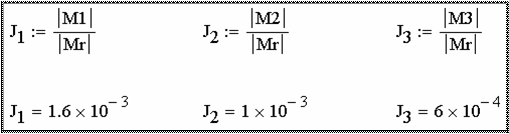 Рис. 2.33
Рис. 2.33


