
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение параметров рабочей точки по внешней характери- стике асинхронного двигателя и нагрузочной характеристике тур- бомеханизма встроенными средствами MathCADСодержание книги
Поиск на нашем сайте
На основе решения задачи, приведённого в предыдущем парагра- фе, покажем определение параметров рабочей точки встроенными сред- ствами MathCAD. Введём разностную функцию (рис. 2.45),
график которой представлен на рис. 2.46.
Разностная функция пересекает ось абсцисс при такой величине ω, которая соответствует искомой. Задача сводится к решению нели- нейного уравнения в окрестности точки ω=154 рад/с, определённой в предыдущем параграфе. Покажем три способа решения. Первый способ представлен на рис. 2.47. Вводим начальное при- ближение ω1=154 рад/с по данным графического решения. Вызываем функцию root. В качестве переменных этой функции указываем разно- стную функцию f1(ω1) и переменную ω1. Функция возвращает ответ ω=154.351 рад/с.
Второй способ представлен на рис. 2.48. Вводим начальное при- ближение ω2=154 рад/с по данным графического решения. Вводим ключевое слово Given. Вводим нелинейное уравнение. Переменной w1 присваиваем результат вычисления функции find. В качестве перемен- ной этой функции указываем переменную ω2. Полученный ответ w1=154.351 рад/с совпадает с ответом, полученным с помощью первого способа.
Третий способ представлен на рис. 2.49. Для решения задачи вы- бран метод дихотомии – метод половинного деления отрезка, на кото- ром ведётся поиск. На первом этапе задаются концы отрезка: ωmin=154 рад/с – начало, ωmax=155 рад/с – конец, что соответствует данным, полу- ченным при графическом решении (рис. 2.44). Задаём функцию fω(∆), где ∆ – точность ответа, с применением элементов программирования, встроенных в MathCAD, доступных для пользователя (см. панель 4, рис. 2.1). В теле программы используются кнопки Add Line (добавить строку программы), ← (локальное определение), while (цикл с условием про- должения), логическое «больше или равно», if(условный оператор), otherwise (оператор «иначе»), функция знака sign(x) (равна 1, если число x положительное, -1 – если x отрицательное и 0, если x=0). Нетрудно проследить работу представленной программы. Чем выше требуется точность ответа, тем больше итераций потребуется для решения задачи. При ∆=0.01 в ответе получим ω=154.351 рад/с.
Подставив ω=154.351 рад/с, найденное одним из вышеописанных способов, в выражение для механической характеристики АД (рис. 2.41), получим вторую искомую координату Mэ=27.355 Нм (рис. 2.50).
В данной главе на примере решения типовой задачи показана возможность автоматизации расчётов с применением MathCAD.
ГЛАВА 8. ПРЯМОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ОПЕРАТОРНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
Операционное исчисление широко применяется для решения за- дач электротехники. Существует множество преобразований, используемых математи- ками: преобразования Лапласа, Карсона, Фурье и другие. Все они име- ют свои достоинства и недостатки, но преобразование Лапласа получи- ло наибольшее распространение – MathCAD имеет встроенную под- держку данного преобразования (рис. 2.51).
Более подробно применение операционного исчисления для ре- шения линейных дифференциальных уравнений и систем можно рас- смотреть в [14]. Рассмотрим подробно вывод операторной передаточной функции однозвенного LC-фильтра низких частот (ФНЧ) (рис. 2.52).
L R
C R НАГР
L = 10 ⋅10−3 Гн C = 100 ⋅10−6 Ф R = 1 Ом
Рис. 2.52
На первом этапе необходимо составить систему дифференциаль- ных уравнений, описывающих состояние ФНЧ. На вход ФНЧ подаётся гармонический сигнал. Будем использовать следующие обозначения переменных: U ВХ (t) - входное напряжение, UВЫХ (t) - выходное напряжение, iL (t) iC (t) iН (t) - ток катушки индуктивности, - ток конденсатора, - ток нагрузки. По второму закону Кирхгофа входное напряжение уравновешива- ется как
(t)⋅ R + U
(t). (2.7) ВХ dt L ВЫХ Согласно первому закону Кирхгофа ток катушки индуктивности iL расщепляется на ток конденсатора iC и ток нагрузки iН iL (t) = iC (t)+ iН (t). (2.8) Известно, что ток конденсатора определяется как
C dt а ток нагрузки по закону Ома выразим как
RНАГР (2.10) Система дифференциальных уравнений, описывающих состояние ФНЧ с учётом 2.7-2.10, выглядит следующим образом
⎧ ⎪ U ВХ ⎪ ⎨
(t) ⋅ R + U
ВЫХ
(t) (2.11)
⎪ i ⎪⎩ L (t) = C dU ВЫХ (t) + U ВЫХ (t).
Применим к выражению 2.11 прямое преобразование Лапласа и получим систему алгебраических уравнений в изображениях и прове- дём алгебраические преобразования ⎧ U ВХ (s) = (L ⋅ s + R)⋅ iL (s)+ U ВЫХ (s) ⎪ ⎨ ⎪ iL
R
⎞ ⎟⋅ U
ВЫХ
(s), (2.12) ⎩ ⎝ НАГР ⎠ где s – оператор Лапласа. Подставим второе уравнение системы (2.12) в первое и проведём алгебраические преобразования U (s) = (L ⋅ s + R)⋅⎛ C ⋅ s + 1 ⎞⋅ U
(s)+ U
(s),
ВЫХ ВЫХ ⎝ RНАГР ⎠
(2.13) ⎛ ⎛ U (s) = (L ⋅ s + R)⋅ C ⋅ s + 1 ⎞ ⎞
(s). ВХ ⎜ ⎜ R ⎟ ⎟ ВЫХ ⎝ ⎝ НАГР ⎠ ⎠ Операторной передаточной функцией ФНЧ W (s) называется от- ношение изображение выходного сигнала U ВЫХ (s) ко входному U ВХ (s)
U ВХ (s) С учётом 2.14 и 2.13 запишем выражение для операторной пере- даточной функции ФНЧ
W (s) =
. 1 ⎞ +1 (2.15)
⎝ RНАГР ⎠
ГЛАВА 9. ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ПЕРЕХОДНЫЕ ФУНКЦИИ
Рассмотрим задачу получения и анализа импульсных переходных характеристик однозвенного нагруженного Г-образного LC -фильтра низких частот (ФНЧ). Пусть ФНЧ коммутируют на источник постоянного тока Uвх при трёх значениях сопротивления нагрузки: 10·R (нагруженный режим), 100·R (нормальный режим), 1000·R (ненагруженный режим) (рис 2.53). Необходимо с применением обратного преобразования Лапласа полу- чить импульсные переходные характеристики для всех значений сопро- тивления нагрузки, определить время переходного процесса и перерегу- лирование. Результаты внести в таблицу.
U ВХ C R НАГР
Рис. 2.53
Вводим в MathCADисходные данные (рис. 2.54).
С учётом (2.15) запишем выражение для выходного напряжения ФНЧ в операторной форме
UВЫХ
s
(L ⋅ s + R)⋅⎛ C ⋅ s +
, 1 ⎞ +1
(2.16)
⎝ RНАГР ⎠
где UВХ
– операторная форма входного напряжения, прикладываемого ступенчато при коммутации ключа (рис. 2.53). Упростим в MathCADвыражение (2.16) с применением оператора упрощения выражений simplify для RНАГР 1 =1000 ⋅ R (рис. 2.55).
К выражению, полученному в результате упрощения, применим обратное преобразование Лапласа с учётом нулевых начальных условий (до коммутации токи и напряжения ФНЧ равны нулю) (рис. 2.56).
Получаем переходную функцию ФНЧ в ненагруженном режиме
⋅ exp (−55 ⋅ t)⋅ 39919 ⋅ sin (5 ⋅ 39919 ⋅ t) и вводим её в MathCAD. Напомним, что операция присвоения в Math- CAD производится как:=. Аналогично получим в MathCADпереходные функции ФНЧ: h 2 (t) h 3(t) – в нормальном (RНАГР 2 = 100 ⋅ R) и – в нагруженном режимах (рис. 2.57).
Как видно из рис. 2.57 переходные процессы имеют колебатель- ный характер с перерегулированием и стремятся при t→∞ к установив- шимся значениям h 1(∞) ≈ h 1(100), h 2 (∞) ≈ h 2 (100), h 3(∞) ≈ h 3(100). Переходный процесс
h 1(t) заканчивается, если h 1(t) ≤1.05 ⋅ h 1(∞) и h 1(t) ≥ 0.95 ⋅ h 1(∞), или, по-другому, h 1(t) последний раз входит в зону допустимых отклонений h 1(∞) ± 0.05 ⋅ h 1(∞). Время переходного про- цесса в MathCADможно определить графически и численно. Переход- ный процесс h 1(t) последний раз пересекает нижнюю границу зоны до- пустимых отклонений при 0.051 с (рис. 2.58), верхнюю – при 0.054 с
Рис. 2.58
Аналогично в MathCADопределяем: – для h 2 (t) время переходного процесса t ПП2 = 0.029 с и – для h 3(t) время переходного процесса t ПП3 = 0.005 с. Перерегулирование для переходной характеристики делим как h 1(t) опре- h 1(tm 1)− h 1(∞) h 1(tm 1)− h 1(100) (2.18)
h 1(∞) h 1(100) где tm 1 – время достижения функцией h 1(t) первого максимума. Для определения tm 1найдём в MathCAD производную
h 1(t) по t
Объявим функцию
dh 1(t) Рис. 2.60
(рис. 2.61).
Графически определим время tm 1в первом приближении (рис. 2.62). tt 1 = 0.00314 c, что соответствует
Используя процедуру findи учитывая (2.18) определяем, что пе- ререгулирование переходной функции (рис. 2.63). h 1(t) составит ∆ h 1 = 84.117%
Аналогично в MathCADопределяем: – для h 2 (t) перерегулирование ∆ h 2 = 73.04% и – для h 3(t) перерегулирование ∆ h 3 = 13.04%. Полученные в данной главе результаты внесём в табл. 2.1. Таблица 2.1
Как видно из табл. 2.1, с увеличением загруженности ФНЧ уменьшается время переходного процесса и перерегулирование.
ГЛАВА 10.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.167.89 (0.013 с.) |

 Рис. 2.45
Рис. 2.45 Рис. 2.46
Рис. 2.46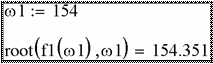 Рис. 2.47
Рис. 2.47 Рис. 2.48
Рис. 2.48 Рис. 2.49
Рис. 2.49 Рис. 2.50
Рис. 2.50 Рис. 2.51
Рис. 2.51
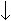 U ВХ (t) =1⋅sin(ω t)
U ВХ (t) =1⋅sin(ω t)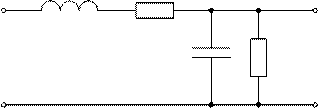

 U ВЫХ
U ВЫХ U (t) = L diL (t) + i
U (t) = L diL (t) + i i (t) = C dU ВЫХ (t), (2.9)
i (t) = C dU ВЫХ (t), (2.9)
 (t) = L diL (t) + i dt L
(t) = L diL (t) + i dt L
 dt RНАГР
dt RНАГР
 ВХ ⎜ ⎟
ВХ ⎜ ⎟ + 1 ⋅ U
+ 1 ⋅ U W (s) = U ВЫХ (s). (2.14)
W (s) = U ВЫХ (s). (2.14) (L ⋅ s + R)⋅⎛ C ⋅ s +
(L ⋅ s + R)⋅⎛ C ⋅ s + ⎜ ⎟
⎜ ⎟ L R
L R Рис. 2.54
Рис. 2.54 (s) = U ВХ
(s) = U ВХ s
s Рис. 2.55
Рис. 2.55 Рис. 2.56
Рис. 2.56

 1001 1001
1001 1001 39919 ⋅ t)−
39919 ⋅ t)− (2.17)
(2.17) − 1000
− 1000 Рис. 2.57
Рис. 2.57 (рис. 2.59), следовательно, t ПП1 = 0.054 с.
(рис. 2.59), следовательно, t ПП1 = 0.054 с.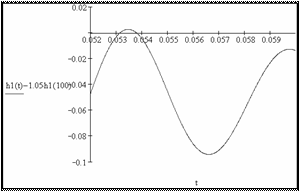 Рис. 2.59
Рис. 2.59
 ∆ h 1 = ⋅100% ≈ ⋅100%,
∆ h 1 = ⋅100% ≈ ⋅100%, (рис. 2.60).
(рис. 2.60). Рис. 2.61
Рис. 2.61 Рис. 2.62
Рис. 2.62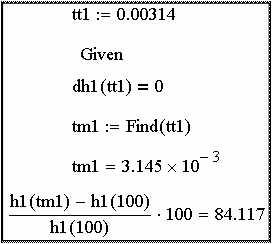 Рис. 2.63
Рис. 2.63


