
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт методом Эйлера переходного процесса пуска вхолостую двигателя постоянного тока независимого возбужденияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть двигатель постоянного тока с независимым возбуждением (ДПТ с НВ) подключается к источнику постоянного тока U(рис. 3.50).
Необходимо рассчитать переходный процесс пуска ДПТ с НВ при пуске вхолостую, определить величины броска тока якоря, наибольший противоток и перерегулирования по скорости в процентах. В начале пе- реходного процесса скорость и ток были равны нулю. Якорная цепь ДПТ с НВ на схеме замещения (рис. 3.50) состоит из: R – суммарного сопротивления якорной цепи, L – суммарной индуктивности якорной цепи, E – электродвижущей силы, пропорциональной скорости вала ω. ЭДС ДПТ с НВ рассчитывается как E = ω⋅ c, (3.41) где c – электромеханический коэффициент ДПТ с НВ. Электромеханический коэффициент определяется как
ω Н где U Н, I Н, ω Н вала ДПТ с НВ. – номинальные напряжение якоря, ток якоря и скорость Система дифференциальных уравнений, описывающих процесс пуска ДПТ с НВ вхолостую, выглядит как
⎪ dt ⎨
+ ω ⋅ c
(3.43)
⎩⎪ dt где J – момент инерции вала двигателя. Явно выделим правые части дифференциальных уравнений
= U − I ⋅ R −ω⋅ c
⎨
(3.44)
= I ⋅ c.
В качестве индексной переменной выберем переменную j. На нулевом шаге имеем исходные данные t 0 = 0, ω0 = 0, I 0 = 0. (3.45) Согласно методу Эйлера на шаге расчёта j+1 имеем следующие соотношения
⎧ ⎪ tj +1 = tj + ∆ t ⎪
(3.46)
⎨ j +1 ⎪
= I j U − I ⋅ R −ω⋅ c
L ⎪ ⎪ω j +1 ⎩
= ω j I ⋅ c
J
J ⋅ R ⋅ L
(3.47) Зададимся численными параметрами для решения задачи в Excel (см. табл. 3.2).
Таблица 3.2
В ячейке A1 рассчитаем коэффициент c (рис. 3.51).
Рис. 3.51
В ячейке B1 рассчитаем шаг интегрирования (рис. 3.52).
Рис. 3.52 В столбце A, начиная с ячейки A3, будет размещён массив време- ни. В столбце B, начиная с ячейки B3, будет размещён массив тока. В столбце C, начиная с ячейки C3, будет размещён массив скорости. В массив A3-C3 внесем нули, так как переходный процесс рассчитывается с нулевыми начальными условиями (рис. 3.53).
Рис. 3.53
Выделим ячейку B1, скопируем содержимое ячейки в буфер с по- мощью сочетания клавиш <Ctrl> + <C>. Вставим содержимое буфера в ячейку A4 с помощью сочетания клавиш <Ctrl> + <V>. В правом ниж- нем углу выберем раскрывающийся маркированный список и в нём от- метим пункт «Значения и форматы чисел». Аналогично внесём скопи- рованную информацию из B1 в E3. Содержимое ячейки E3 удвоим (рис. 3. 54).
Рис. 3.54
Удвоенное значение шага интегрирования внесём в ячейку А5, выделив в параметрах вставки пункт «Значения и форматы чисел». Вы- делим ячейки A4-A5 и продолжим выделение до ячейки A250. В ячейку B4 внесём формулу для второй итерации расчёта тока (рис. 3.55).
Рис. 3.55 В ячейку C4 внесём формулу для второй итерации расчёта скоро- сти (рис. 3.56).
Рис. 3.56
Выделим массив ячеек A4-C4 и продолжим выделение до A250- C250. Получен числовой массив решения системы дифференциальных уравнений. Выделим массив A3-C250. Вызовем «мастер диаграмм», по аналогии с предыдущими диаграммами построим графики переходных процессов тока и скорости (рис. 3.57).
Рис. 3.57
Определим величину броска тока. Для этого в ячейку F3 вставим функцию МАКС из категории «Статистические». В меню функции вве- дём диапазон значений тока: B3-B250.
Рис. 3.58
В ячейке F3 получим величину броска тока якоря: 135,7589 А (рис. 3.59).
Рис. 3.59
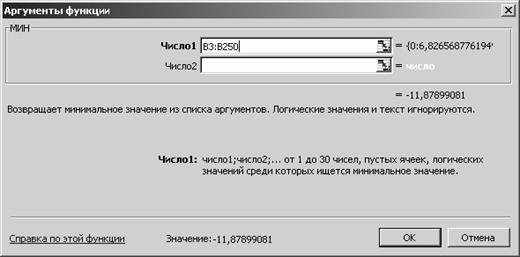
Определим максимум противотока или минимум тока и запишем его в ячейке G3. Для этого воспользуемся функцией МИН из категории «Статистические». В меню функции выделяем диапазон B3-B250 (рис. 3.60).
Рис. 3.60 Величина противотока составит -11.879 А (рис. 3.61).
Рис. 3.61
Определим перерегулирование по скорости как
−ω У
⋅100%,.
где ω М ω У ω У – максимальная скорость во время переходного процесса,
– установившаяся скорость. (3.48) Установившаяся скорость в данной задаче равна номинальной ω У = 157 рад/с. Для определения максимальной скорости в ячейку H3 введём функцию МАКС с диапазоном C3-C250 (рис. 3. 62).
Рис. 3.62
В ячейке I3 согласно (3.48) рассчитаем, что перерегулирование по скорости при пуске ДПТ с НВ составит 19.626% (рис. 3.63).
Рис. 3.63
Итак в данной главе средствами Excel рассчитан переходный про- цесс пуска ДПТ с НВ, определено, что бросок тока и противоток соста- вят соответственно 135,7589 А и -11.879 А, перерегулирование составит 19.626%. ГЛАВА 6. ПОСТРОЕНИЕ ХАРАКТЕРИСТИК В ПРОГРАММЕ EXCEL, ЗА- ГРУЖАЕМЫХ ИЗ ВНЕШНИХ ФАЙЛОВ
Пусть имеется файл с расчётными или экспериментальными дан- ными, полученными из различных источников – из прикладной программы, например «Electronics Workbench» (EWB), MathCAD, Matlab, Maple и т. п., – из цифрового осциллографа. Необходимо изменить расширение файла с данными на такое, ко- торое будет доступно программе Excel, например на *.xls. Далее произ- водим загрузку файла в Excel. На рис. 3.64 приведен пример загрузки в Excel данных из файла OE_upt.xls (см. раздел 1, посвящённый EWB). На рисунке приведены только первые десять строк.
Рис. 3.64
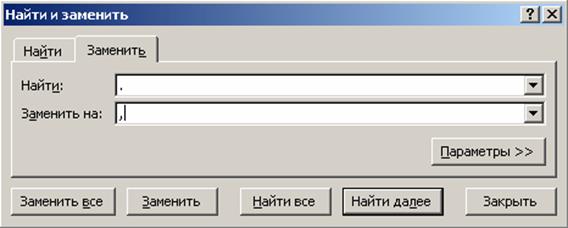
В качестве разделителя целой и дробной части числа в Excel должна быть использована запятая, а не точка, поэтому необходимо произвести замену точек на запятые во всём файле. При нажатии кла- виш <Ctrl> + <H> появляется диалоговое окно «Найти и заменить» (рис. П1.2). После ввода точки в поле «Найти» и ввода запятой в поле «Заменить на:» необходимо нажать кнопку «Заменить всё».
Рис. 3.65
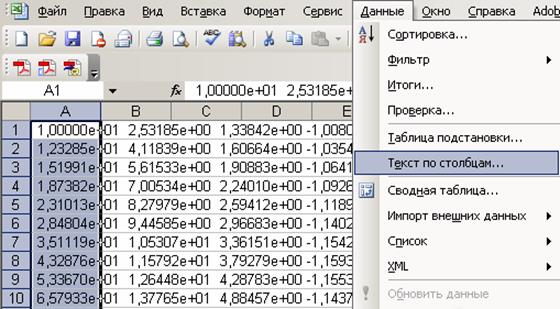
Из рис. 3.64, на примере выделенной ячейки A1 видно, что дан- ные располагаются в одном столбце A и каждая ячейка содержит четы- ре числа, разделённых пробелом. Необходимо разделить данные по столбцам так, чтобы в одной ячейке было записано одно число. Для это- го выделяем данные в столбце A и в разделе меню «Данные» выбираем подраздел «Текст по столбцам» (рис. 3.66).
Рис. 3.66
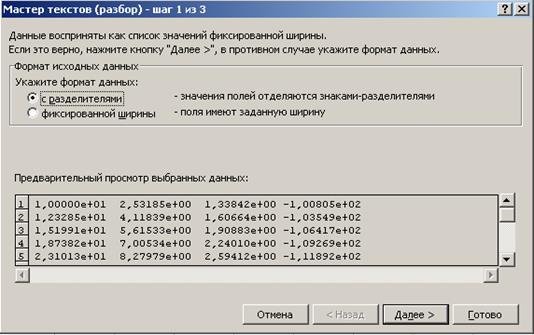
Появляется диалоговое окно «Мастер текстов (разбор) – шаг 1 из 3» (рис. 3.67). В разделе меню «Формат исходных данных» укажите формат данных «с разделителями» и нажмите кнопку «Далее». Поя- вится следующее диалоговое окно «Мастер текстов (разбор) – шаг 2 из 3» (рис. 3.68).
Рис. 3.67
Рис. 3.68 Отметьте в диалоговом окне, что символом-разделителем являет- ся пробел, ограничителем строк является апостроф «”» и необходимо считать последовательные разделители одним. Нажмите кнопку «Да- лее». Появится диалоговое окно «Мастер текстов (разбор) – шаг 3 из 3» (рис. 3.69). Нажать кнопку «Готово».
Рис. 3.69
Выделить область данных. С помощью сочетания клавиш <Ctrl>+<1> вызвать диалоговое окно «Формат ячеек» (рис. 3.70). Вы- брать вкладку «Число», отметить числовой формат «Общий» и нажать кнопку «Ок». В столбце B будет расположен аргумент частотной харак- теристики – частота, измеряемая в Герцах (Гц). В столбце C будет рас- положена логарифмическая амплитудно-частотная характеристика (ЛАЧХ) усилителя переменного тока (УПТ), измеряемая в децибелах (дБ). В столбце D будет расположена амплитудно-частотная характери- стика (АЧХ) УПТ, измеряемая в относительных единицах (безразмер- ная). В столбце E будет расположена фазо-частотная характеристика (ФЧХ) УПТ, измеряемая в градусах угловой шкалы. Для построения ЛАЧХ выделим данные в столбце C. В основном меню выделим раздел «Вставка».
Рис. 3.70
Рис. 3.71 На вкладке «Нестандартные» выбираем тип диаграммы «Лога- рифмическая» и нажимаем кнопку «Далее». Затем выполняются шаги 2, 3 и 4 диалогового окна «Мастер диаграмм» и получаем ЛАЧХ УПТ (рис. 3.72).
Рис. 3.72. Логарифмическая АЧХ УПТ, построенная в Excel
ЛАЧХ, полученную в Excel, можно вставить в текстовый редактор Word. Для этого с помощью сочетания клавиш < Alt > + < Print Screen > или < Print Screen > помещаем копию экрана в буфер. Затем копию экра- на вставляем в один из графических редакторов, например Adobe Photo- shop, Paint или другой им подобный. После обработки копии экрана по- лучаем рисунок, подобный рис. 3.72. АЧХ и ФЧХ построенные в Excel с помощью стандартных диа- грамм, приведены на рис. 1.24-1.26 и 3.72. ГЛАВА 7. ПРАКТИЧЕСКАЯ РАБОТА «РЕШЕНИЕ ТИПОВЫХ ЭЛЕКТРОТЕХНИЧЕСКИХ ЗАДАЧ В ПРОГРАММЕ EXCEL»
Цель работы: получение практических навыков решения числен- ных задач средствами программы Excel.
Работа выполняется каждым студентом самостоятельно. Номерварианта определяется по последней цифре номера зачётной книжкистудента. Решить в Excel задания, приведённые в программе работы.
Программа работы
Тема 1.
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 463; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.205.149 (0.008 с.) |

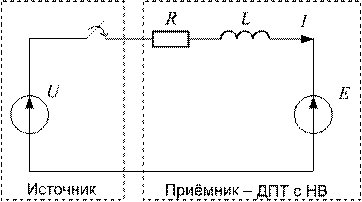 Рис. 3.50
Рис. 3.50 c = UН − IН ⋅ R, (3.42)
c = UН − IН ⋅ R, (3.42)
 ⎪ I ⋅ c = J ⋅ d ω,
⎪ I ⋅ c = J ⋅ d ω, ⎧ dI
⎧ dI ⎪ dt L
⎪ dt L ⎪⎩ dt J
⎪⎩ dt J + ∆ t ⋅ j j
+ ∆ t ⋅ j j + ∆ t ⋅ j.
+ ∆ t ⋅ j. Шаг интегрирования рассчитаем следующим образом
Шаг интегрирования рассчитаем следующим образом









 ∆ω%= ω М
∆ω%= ω М




 В этом разделе запустим подраздел «Диаграмма». Появляется диалоговое окно «Мастер диаграмм (шаг 1 из 4): тип диаграммы» (рис. 3.71).
В этом разделе запустим подраздел «Диаграмма». Появляется диалоговое окно «Мастер диаграмм (шаг 1 из 4): тип диаграммы» (рис. 3.71).




