
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 6. Частотные характеристикиСодержание книги
Поиск на нашем сайте
Понятие частотных характеристик Если подать на вход системы с передаточной функцией W(p) гармонический сигнал
то после завершения переходного процесса на выходе установится гармонические колебания
с той же частотой Подставим выражения для x(t) и y(t) в уравнение динамики (aоpn + a1pn - 1 + a2pn - 2 +... + an) y = (bоpm + b1pm-1 +... + bm) x. Учтем, что
а значит pnx = pnUmejwt = Um (jw)n e jwt = (jw)n x. Аналогичные соотношения можно записать и для левой части уравнения. Получим:
По аналогии с передаточной функцией можно записать:
W(j
W(j
где P(
 ( ( ) - фазовая ЧХ (ФЧХ): ) - фазовая ЧХ (ФЧХ):
АЧХ дает отношение амплитуд выходного и входного сигналов, ФЧХ - сдвиг по фазе выходной величины относительно входной. Если W(j
В ТАУ широко используются логарифмические частотные характеристики (ЛЧХ) (рис.49): логарифмическая амплитудная ЧХ (ЛАЧХ) L(  ) и логарифмическая фазовая ЧХ (ЛФЧХ) ) и логарифмическая фазовая ЧХ (ЛФЧХ)  . Они получаются путем логарифмирования передаточной функции: . Они получаются путем логарифмирования передаточной функции:
ЛАЧХ получают из первого слагаемого, которое из соображений масштабирования умножается на 20, и используют не натуральный логарифм, а десятичный, то есть L(
lg(P2/P1) = lg(A22/A12) = 20lg(A2/A1). По оси абсцисс откладывается частота
ЛФЧХ, получаемая из второго слагаемого, отличается от ФЧХ только масштабом по оси ЧХ являются исчерпывающими характеристиками системы. Зная ЧХ системы можно восстановить ее передаточную функцию и определить параметры. Частотные характеристики типовых звеньев Зная передаточную функцию звена W(p) легко получить все его частотные характеристики. Для этого необходимо подставить в нее j
Безынерционное звено Передаточная функция: W(p) = k. АФЧХ: W(j ВЧХ: P( МЧХ: Q( АЧХ: A( ФЧХ: ЛАЧХ: L(
Некоторые ЧХ показаны на рис.50. Звено пропускает все частоты одинаково c увеличением амплитуды в k раз и без сдвига по фазе.
Интегрирующее звено
Передаточная функция: W(p) = k/p. Рассмотрим частный случай, когда k = 1, то есть W(p) = 1/p. АФЧХ: ВЧХ: P( МЧХ: Q( АЧХ: A( ФЧХ: ЛАЧХ: L( ЧХ показаны на рис.51. Все частоты звено пропускает с запаздыванием по фазе на 90о. Амплитуда выходного сигнала увеличивается при уменьшении частоты, и уменьшается до нуля при росте частоты (звено "заваливает" высокие частоты). ЛАЧХ представляет собой прямую, про
ходящую через точку L(  ) = 0 при ) = 0 при  = 1. При увеличении частоты на декаду ордината уменьшается на 20lg10 = 20дб, то есть наклон ЛАЧХ равен - 20 дб/дек (децибел на декаду). = 1. При увеличении частоты на декаду ордината уменьшается на 20lg10 = 20дб, то есть наклон ЛАЧХ равен - 20 дб/дек (децибел на декаду).
Апериодическое звено При k = 1 получаем следующие выражения ЧХ:
;
Здесь A1 и A2 - амплитуды числителя и знаменателя ЛФЧХ; ЛФЧХ: L( ЧХ показаны на рис.52.
АФЧХ есть полуокружность радиусом 1/2 с центром в точке P = 1/2. При построении асимптотической ЛАЧХ считают, что при ЛФЧХ асимптотически стремится к нулю при уменьшении w до нуля (чем меньше частота, тем меньше искажения сигнала по фазе) и к -
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.37.178 (0.009 с.) |

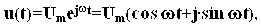
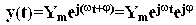

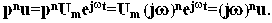
 .
.



 от 0 до +
от 0 до + 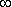 его конец будет вычерчивать кривую, называемую годографом вектора W(j
его конец будет вычерчивать кривую, называемую годографом вектора W(j  от -
от - 

 откладывается по оси ординат в градусах или радианах. Для элементарных звеньев она не выходит за пределы: -p ≤
откладывается по оси ординат в градусах или радианах. Для элементарных звеньев она не выходит за пределы: -p ≤ 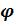 ≤+p.
≤+p.

 /2.
/2.
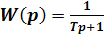 ;
;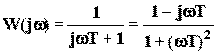
 ;
; ;
;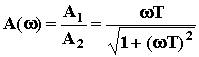 ;
;
 - 10lg1 = 0.. При
- 10lg1 = 0.. При 


