
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотные характеристики разомкнутых одноконтурных САУСодержание книги
Поиск на нашем сайте
При исследовании и проектировании САУ часто используют АФЧХ, ЛАЧХ и ЛФЧХ разомкнутых систем. Это объясняется тем, что разомкнутые САУ более просто исследовать экспериментально, чем замкнутые. В то же время по ним можно получить исчерпывающую информацию о поведении данной САУ в замкнутом состоянии. Любую многоконтурную САУ можно привести к одноконтурной. Разомкнутая одноконтурная САУ состоит из цепочки последовательно соединенных динамических звеньев. Зная передаточную функцию разомкнутой САУ можно построить ее ЧХ. И наоборот, зная ЧХ разомкнутой САУ, снятую, например, опытным путем, можно найти ее передаточную функцию. Передаточная функция разомкнутой одноконтурной системы равна произведению передаточных функций отдельных звеньев:
Заменив в этом выражении p на j w получим ее АФЧХ:
АЧХ: значит ЛАЧХ равна сумме ЛАЧХ звеньев: ЛФЧХ: Таким образом ЛАЧХ и ЛФЧХ разомкнутой САУ строят путем графического сложения ЛАЧХ и ЛФЧХ звеньев. При этом ограничиваются построением асимптотической ЛАЧХ. Для построения ЛАЧХ и ЛФЧХ рекомендуется следующий порядок: 1. раскладывают сложную передаточную функцию на множители, являющиеся передаточными функциями типовых динамических звеньев (порядок полиномов числителя и знаменателя не выше второго); 2. вычисляют сопрягающие частоты отдельных звеньев и строят асимптотические ЛАЧХ и ЛФЧХ каждого элементарного звена; 3. путем графического суммирования ЛАЧХ и ЛФЧХ звеньев строят результирующие ЧХ.
Рассмотрим конкретный пример: W(p) = Раскладываем данную передаточную функцию на передаточные функции элементарных звеньев: 1) безынерционное звено: W1 = K1 = 100 => L(w) = 20lg100 = 40; 2) форсирующее звено: W2 = p + 1; его параметры: K2 = 1, T2 = 1, 3) интегрирующее звено: W3 = 1/p; его ЛАЧХ проходит через точку L = 0 при частоте 4) апериодическое звено: W4 = 1/(0.1p + 1); его параметры: K4 = 1, T4 = 0.1, Порядок построения ЛАЧХ и ЛФЧХ показан на рис.57.
Иногда требуется решить обратную задачу, то есть определить передаточную функцию по известной ЛАЧХ. Процедура определения передаточной функции состоит из следующих этапов: 1) известная ЛАЧХ представляется в асимптотическом виде, для этого непрерывная кривая заменяется отрезками прямых либо горизонтальных, либо с наклоном, кратным ±20 дб/дек; 2) асимптотическая ЛАЧХ раскладывается на ЛАЧХ элементарных звеньев; 3) для каждой из полученных ЛАЧХ определяются k и 4) передаточная функция САУ определяем путем перемножения передаточных функций типовых звеньев.
Описанный порядок иллюстрируется на рис.58. Здесь ЛАЧХ может быть представлена суммой ЛАЧХ четырех типовых звеньев: пропорционального W1 = 100, апериодического W2 = 1/(p + 1), форсирующего W3 = 0.1p + 1 и апериодического W4 = 1/(0.01p + 1). Таким образом, передаточная функция разомкнутой САУ имеет вид
В более сложных случаях наклоны ЛАЧХ на некоторых участках превышают ± 20дб/дек. Тогда помимо параметров K и T приходится определять еще и коэффициенты демпфирования r. Зная передаточную функцию разомкнутой САУ можно построить ее уравнение динамики
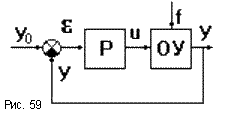
Таким образом можно определить уравнение динамики реальных звеньев и всей реальной САУ, если оно теоретически это сделать затруднительно. Для снятия частотных характеристик реальной разомкнутой САУ на ее вход подают гармонический сигнал с изменяемой частотой и определяют изменение амплитуды и фазы выходного сигнала в зависимости от частоты. По полученным характеристикам определяют уравнение динамики, после чего САУ можно исследовать теоретически. Законы регулирования Пусть задана какая-то САР (рис.59).
Законом регулирования называется математическая зависимость, в соответствии с которой
управляющее воздействие на объект вырабатывалось бы безынерционным регулятором.
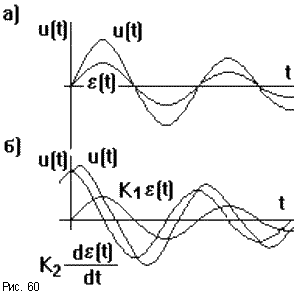
Простейшим из них является пропорциональный закон регулирования, при котором u(t) = Ke(t) (рис.60а), где u(t) - это управляющее воздействие, формируемое регулятором, e(t) - отклонение регулируемой величины от требуемого значения, K - коэффициент пропорциональности регулятора Р.
То есть для создания управляющего воздействия необходимо наличие ошибки регулирования и чтобы величина этой ошибки была пропорциональна возмущающему воздействию f(t). Другими словами САУ в целом должна быть статической. Такие регуляторы называют П-регуляторами. Так как при воздействии возмущения на объект управления отклонение регулируемой величины от требуемого значения происходит с конечной скоростью (рис.60б), то в начальный момент на вход регулятора подается очень малая величина e, вызывая при этом слабые управляющие воздействия u. Для повышения быстродействия системы желательно форсировать процесс управления. Для этого в регулятор вводят звенья, формирующие на выходе сигнал, пропорциональный производной от входной величины, то есть дифференцирующие или форсирующие звенья. Такой закон регулирования называется пропорционально - дифференциальным: u(t) = K1e(t) + K2 В соответствии с ним работают ПД-регуляторы. Чем быстрее нарастает отклонение регулируемой величины от требуемого значения, тем интенсивнее работает ПД-регулятор, что препятствует дальнейшему нарастанию данного отклонения. Кроме того при увеличении отклонения (de(t)/dt > 0) управляющий сигнал u будет больше, чем при уменьшении (de(t)/dt < 0), что также играет положительную роль, снижая колебательность процеса управления. Добавление в регулятор двух дифференцирующих звеньев позволяет формировать управляющее воздействие по второй производной отклонения e, такой регулятор называется ПДД-регулятором. Интегральный закон регулирования реализуется И-регулятором, его формулировка:
Этот регулятор наращивает управляющее воздействие до тех пор пока управляемая величина отличается от требуемого значения, то есть пока e(t) И-регулятор обеспечивает астатическое регулирование. При малых e управляющее воздействие изменяется с малой скоростью, поэтому данный регулятор очень инерционный. Чтобы увеличить быстродействие обычно последовательно с ним включают усилитель, это дает пропорционально-интегральный закон регулирования (ПИ-регулятор), его формула:
Первое слагаемое обеспечивает быстродействие, второе - астатичность, то есть точность регулирования. Еще большее быстродействие обеспечивается при добавлении слагаемого, пропорционального производной от отклонения управляемой величины de/dt, такой закон регулирования обеспечивается ПИД-регулятором, его формула:
. Контрольные вопросы
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.123.10 (0.009 с.) |

 .
.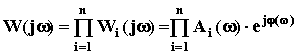 .
.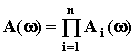 ,
, .
.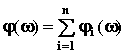 .
.
 = W1W2W3W4.
= W1W2W3W4. 2 = 1/T2 = 1;
2 = 1/T2 = 1;
 .
.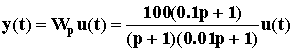 =>
=>  =>
=> =>
=>  .
.
 de(t)/dt.
de(t)/dt. .
. 0.
0. .
.
 .
. 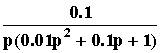 .
. 


