
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 4. Структурные схемы САУСодержание книги
Поиск на нашем сайте
4.1. Эквивалентные преобразования структурных схем
Структурная схема САУ в простейшем случае строится из элементарных динамических звеньев. Но несколько элементарных звеньев могут быть заменены одним звеном со сложной передаточной функцией. Для этого существуют правила эквивалентного преобразования структурных схем. Рассмотрим возможные способы преобразований. 1. Последовательное соединение (рис.28) - выходная величина предшествующего звена подается на вход последующего.
При этом можно записать: y1 = W1 yn = W1 Таким образом, есть цепочка последовательно соединенных звеньев преобразуется в эквивалентное звено с передаточной функцией, равной произведению передаточных функций отдельных звеньев. 2. Параллельно - согласное соединение (рис.29) - на вход каждого звена подается один и тот же сигнал, а выходные сигналы складываются.
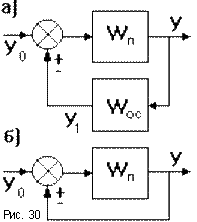
Тогда: y = y1 + y2 +... + yn = (W1 + W2 +... + W3) yo = Wэкв То есть цепочка звеньев, соединенных параллельно - согласно, преобразуется в звено с передаточной функцией, равной сумме передаточных функций отдельных звеньев. 3. Параллельно - встречное соединение (рис. 30а) - звено охвачено положительной или отрицательной обратной связью. Участок цепи, по которому сигнал идет в противоположном направлении по отношению к системе в целом (то есть с выхода на вход) называется цепью обратной связи с передаточной функцией Wос.
При этом для отрицательной обратной связи:
следовательно
Аналогично: Если Замкнутую систему называют одноконтурной, если при ее размыкании в какой либо точке получают цепочку из последовательно соединенных элементов (рис.31а). Участок цепи, состоящий из последовательно соединенных звеньев, соединяющий точку приложения входного сигнала с точкой съема выходного сигнала называется прямой цепью (рис.31б, передаточная функция прямой цепи Wп = Wo
системы с отрицательной ОС равна передаточной функции прямой цепи, деленной на единицу плюс передаточная функция разомкнутой цепи. Для положительной ОС в знаменателе знак минус.
Если сменить точку снятия выходного сигнала, то меняется вид прямой цепи. Так, если считать выходным сигнал y1 на выходе звена W1, то Wp = Wo Замкнутые системы бывают одноконтурными и многоконтурной (рис.32).Чтобы найти эквивалентную передаточную функцию для данной схемы нужно сначала осуществить преобразование
отдельных участков. Если многоконтурная система имеет перекрещивающиеся связи (рис.33), то для вычисле
ния эквивалентной передаточной функции нужны дополнительные правила:
4. При переносе сумматора через звено по ходу сигнала необходимо добавить звено с передаточной функцией того звена, через которое переносится сумматор. Если сумматор переносится против хода сигнала, то добавляется звено с передаточной функцией, обратной передаточной функции звена, через которое переносим сумматор (рис.34).
Так с выхода системы на рис.34а снимается сигнал y2 = (f + yo W1) W2. Такой же сигнал должен сниматься с выходов систем на рис.34б: y2 = f W2 + yo W1 W2 = (f + yo W1) W2,
и на рис.34в: y2 = (f (1/W1) + yo) W1 W2 = (f + yo W1) W2. При подобных преобразованиях могут возникать неэквивалентные участки линии связи (на рисунках они заштрихованы). 4. При переносе узла через звено по ходу сигнала добавляется звено с передаточной функцией, обратной передаточной функции звена, через которое переносим узел. Если узел переносится против хода сигнала, то добавляется звено с передаточной функцией звена, через которое переносится узел (рис.35).
Так с выхода системы на рис.35а снимается сигнал y1 = yoW1. Такой же сигнал снимается с выходов рис.35б: y1 = yoW1W2/W2 = yoW1 и рис.35в: y1 = yoW1. 5. Возможны взаимные перестановки узлов и сумматоров: узлы можно менять местами (рис. 36а); сумматоры тоже можно менять местами (рис.36б); при переносе узла через сумматор необходимо добавить сравнивающий элемент (рис.36в: y = y1 + f1 = > y1 = y - f1) или сумматор
(рис.36г: y = y1 + f1).
Во всех случаях переноса элементов структурной схемы возникают неэквивалентные участки линии связи, поэтому надо быть осторожным в местах съема выходного сигнала. При эквивалентных преобразованиях одной и той же структурной схемы могут быть получены различные передаточные функции системы по разным входам и выходам. Так на рис.48 имеется два входа: по управляющему воздействию x и возмущению f при одном выходе y. Такая схема может быть преобразована к одному звену с двумя передаточными функциями Wuy и Wfy.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.117.89 (0.008 с.) |


 yo; y2 = W2
yo; y2 = W2  .
.
 .
.
 ;
;  ;
; 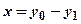 ,
, = >
= > = >
= >  , где
, где  .
. - для положительной обратной связи.
- для положительной обратной связи. , то обратная связь называется единичной (рис.30б), тогда
, то обратная связь называется единичной (рис.30б), тогда  .
.








