
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 1. От классических задач регулирования к интеллектуальному управлениюСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Введение Лекция 1. От классических задач регулирования к интеллектуальному управлению 1.1. Основные определения Согласно определению, данному выдающимся ученым А.М. Летовым[1], теория управления «есть совокупность методов, позволяющих выработать и обосновать решение, которое принимается для достижения заранее поставленной цели, в условиях как-либо определенной ситуации». В частности, теория автоматического управления – «наука о методах определения законов управления какими-либо объектами, допускающих реализацию с помощью технических средств автоматики». Часть 1. Классическая теория автоматического управления Лекция 2. Основные принципы автоматического управления Общие понятия Управление каким-либо объектом (объект управления будем обозначать ОУ) есть воздействие на него в целях достижения требуемых состояний или процессов. В качестве объекта управления может служить самолет, станок, электродвигатель и т.п. Управление объектом с помощью технических средств без участия человека называется автоматическим управлением. Совокупность объекта управления и средств автоматического управления называется системой автоматического управления (САУ).
Теория автоматического управления (ТАУ) появилась во второй половине 19 века сначала как теория регулирования. Широкое применение паровых машин вызвало потребность в регуляторах, то есть в специальных устройствах, поддерживающих устойчивый режим работы паровой машины. Это дало начало научным исследованиям в области управления техническими объектами. Оказалось, что результаты и выводы данной теории могут быть применимы к управлению объектами различной природы с различными принципами действия. В настоящее время сфера ее влияния расширилась на анализ динамики таких систем, как экономические, социальные и т.п. Поэтому прежнее название «Теория автоматического регулирования» заменено на более широкое – «Теория автоматического управления».
Основной задачей автоматического управления является поддержание определенного закона изменения одной или нескольких физических величин, характеризующих процессы, протекающие в объекте управления, без непосредственного участия человека. Эти величины называются управляемыми величинами. Если в качестве объекта управления рассматривается хлебопекарная печь, то управляемой величиной будет температура, которая должна изменяться по заданной программе в соответствии с требованиями технологического процесса.
Фундаментальные принципы управления
Принято различать три фундаментальных принципа управления: принцип разомкнутого управления, принцип компенсации, принцип обратной связи.
Принцип компенсации
Если возмущающий фактор искажает выходную величину до недопустимых пределов, то применяют принцип компенсации (рис.6, КУ - корректирующее устройство).
Пусть yо - значение выходной величины, которое требуется обеспечить согласно программе. На самом деле из-за возмущения f на выходе регистрируется значение y. Величина e = yо - y называется отклонением от заданной величины. Если каким-то образом удается измерить величину f, то можно откорректировать управляющее воздействие х на входе объекта управления, суммируя сигнал устройства управления с корректирующим воздействием, пропорциональным возмущению f и компенсирующим его влияние. Примеры систем компенсации: биметаллический маятник в часах, компенсационная обмотка машины постоянного тока и т.п. На рис.6 в цепи нагревательного элемента (НЭ) стоит термосопротивление R t, величина которого меняется в зависимости от колебаний температуры окружающей среды, корректируя напряжение на нагревательном элементе. Достоинство принципа компенсации: быстрота реакции на возмущения. Он более точен, чем принцип разомкнутого управления. Недостаток: невозможность учета подобным образом всех возможных возмущений. Принцип обратной связи
Наибольшее распространение в технике получил принцип обратной связи (рис.7). Здесь управляющее воздействие корректируется в зависимости от выходной величины y(t). И уже не важно, какие возмущения действуют на объект управления. Если значение y(t) отклоняется от требуемого, то происходит корректировка сигнала х(t) с целью уменьшения данного отклонения. Связь выхода объекта управления с его входом называется главной обратной связью (ОС).
В частном случае (рис.8) задающее формирует требуемое значение выходной величины yо(t), которое сравнивается с действительным значением на выходе САУ y(t).
Отклонение e = yо - y с выхода сравнивающего устройства подается на вход регулятора (Р), объединяющего в себе устройство управления (УУ), управляющий орган (УО), чувствительный элемент (ЧЭ). Если e ≠ 0, то регулятор формирует управляющее воздействие х(t), действующее до тех пор, пока не обеспечится равенство e = 0, или y = yо. Так как на регулятор подается разность сигналов, то такая обратная связь называется отрицательной, в отличие от положительной обратной связи, когда сигналы складываются. Такое управление в функции отклонения называется регулированием, а подобную САУ называют системой автоматического регулирования (САР). Так на рис.9 изображена упрощенная схема САР хлебопекарной печи.
Роль задающего устройства здесь выполняет потенциометр, напряжение на котором U з сравнивается с напряжением на термопаре U т. Их разность DU через усилитель подается на исполнительный двигатель (ИД), регулирующий через редуктор положение движка реостата в цепи нагревательного элемента (НЭ). Наличие усилителя говорит о том, что данная САР является системой непрямого регулирования, так как энергия для функций управления берется от посторонних источников питания, в отличие от систем прямого регулирования, в которых энергия берется непосредственно от объекта управления, как, например, в САР уровня воды в баке (рис.10).
Недостатком принципа обратной связи является инерционность системы. Поэтому часто применяют комбинацию данного принципа с принципом компенсации, что позволяет объединить достоинства обоих принципов: быстроту реакции на возмущение принципа компенсации и точность регулирования независимо от природы возмущений принципа обратной связи. Контрольные вопросы 1. Что называется управлением? 2. Что называется автоматическим управлением? 3. Что называется системой автоматического управления? 4. Что является основной задачей автоматического управления? 5. Что называется объектом управления? 6. Что называется управляемой величиной? 7. Что называется управляющим органом? 8. Что называется чувствительным элементом? 9. Что такое входная и выходная величины? 10. Что называется управляющим воздействием? 11. Что называется возмущением? 12. Что называется отклонением от заданной величины? 13. Что называется управляющим устройством? 14. Что называется задающим устройством? 15. Что называется функциональной схемой и из чего она состоит? 16. В чем отличие сигнала от физической величины? 17. В чем суть принципа разомкнутого управления? 18. В чем суть принципа компенсации? 19. В чем суть принципа обратной связи? 20. Перечислите достоинства и недостатки принципов управления? 21. Какой частный случай управления называется регулированием? 22. В чем отличие систем прямого и непрямого регулирования? Общие понятия
В зависимости от принципа и закона функционирования задающего устройства, определяющего программу изменения выходной величины, различают основные виды САУ: системы стабилизации, программные, следящие и самонастраивающиеся системы, среди которых можно выделить экстремальные, оптимальные и адаптивные системы.
В системах стабилизации (рис. 9, 10) обеспечивается неизменное значение управляемой величины при всех видах возмущений, т.е. y(t) = const. Задающее устройство формирует эталонный сигнал, с которым сравнивается выходная величина. Задающее устройство, как правило, допускает настройку эталонного сигнала, что позволяет менять по желанию значение выходной величины.
В программных системах обеспечивается изменение управляемой величины в соответствии с программой, формируемой задающим устройством. В качестве задающего устройства может использоваться кулачковый механизм, устройство считывания с перфоленты или магнитной ленты и т.п. К этому виду САУ можно отнести заводные игрушки, магнитофоны, проигрыватели и т.п. Различают системы с временной программой (например, рис. 1), обеспечивающие y = f(t), и системы с пространственной программой, в которых y = f(x), применяемые там, где на выходе САУ важно получить требуемую траекторию в пространстве, например, в копировальном станке (рис. 11), закон движения во времени здесь роли не играет.
Следящие системы отличаются от программных лишь тем, что программа y = f(t) или y = f(x) заранее неизвестна. В качестве задающего выступает устройство, следящее за изменением какого-либо внешнего параметра. Эти изменения и будут определять изменения выходной величины САУ. Например, рука робота, повторяющая движения руки человека.
Все три рассмотренные вида САУ могут быть построены по любому из трех фундаментальных принципов управления. Для них характерно требование совпадения выходной величины с некоторым предписанным значением на входе САУ, которое само может меняться. То есть в любой момент времени требуемое значение выходной величины определено однозначно. В самонастраивающихся системах задающее устройство ищет такое значение управляемой величины, которое в каком-то смысле является оптимальным.
Так в экстремальных системах (рис.12) требуется, чтобы выходная величина всегда принимала экстремальное значение из всех возможных, которое заранее не определено и может непредсказуемо изменяться. Для его поиска система выполняет небольшие пробные движения и анализирует реакцию выходной величины на эти пробы. После этого вырабатывается управляющее воздействие, приближающее выходную величину к экстремальному значению. Процесс повторяется непрерывно. Так как в данных САУ происходит непрерывная оценка выходного параметра, то они выполняются только в соответствии с третьим принципом управления: принципом обратной связи. Оптимальные системы являются более сложным вариантом экстремальных систем. Здесь происходит, как правило, сложная обработка информации о характере изменения выходных величин и возмущений, о характере влияния управляющих воздействий на выходные величины, может быть задействована теоретическая информация, информация эвристического характера и т.п. Поэтому основным отличием экстремальных систем является использование компьютера. Эти системы могут работать в соответствии с любым из трех фундаментальных принципов управления.
В адаптивных системах предусмотрена возможность автоматической перенастройки параметров или изменения принципиальной схемы САУ с целью приспособления к изменяющимся внешним условиям. В соответствии с этим различают самонастраивающиеся и самоорганизующиеся адаптивные системы.
Все виды САУ обеспечивают совпадение выходной величины с требуемым значением. Отличие лишь в программе изменения требуемого значения. Поэтому основы ТАУ строятся на анализе самых простых систем: систем стабилизации. Научившись анализировать динамические свойства САУ, мы учтем все особенности более сложных видов САУ. Статические характеристики
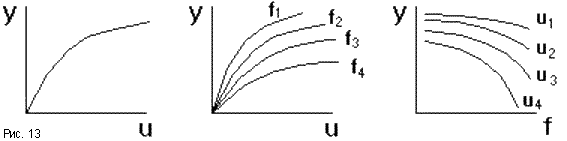
Режим работы САУ, в котором управляемая величина и все промежуточные величины не изменяются во времени, называется установившимся, или статическим режимом. Любое звено и САУ в целом в данном режиме описывается уравнениями статики вида y = F(х, f), в которых отсутствует время t. Соответствующие им графики называются статическими характеристиками. Статическая характеристика звена с одним входом х может быть представлена кривой y = F(х) (рис.13). Если звено имеет второй вход по возмущению f, то статическая характеристика задается семейством кривых y = F(х) при различных значениях f, или y = F(f) при различных х.
Так примером одного из функциональных звеньев системы регулирования воды в баке (см. выше) является обычный рычаг (рис.14). Уравнение статики для него имеет вид y = K х. Его можно изобразить звеном, функцией которого является усиление (или ослабление) входного сигнала в K раз. Коэффициент K = y / х, равный отношению выходной величины к входной называется коэффициентом усиления звена. Когда входная и выходная величины имеют разную природу, его называют коэффициентом передачи.
Статическая характеристика данного звена имеет вид отрезка прямой линии с наклоном a = arctg (L2/L1) = arctg (K) (рис.15). Звенья с линейными статическими характеристиками называются линейными. Статические характеристики реальных звеньев, как правило, нелинейны. Такие звенья называются нелинейными. Для них характерна зависимость коэффициента передачи от величины входного сигнала: K = Dy / Dх ≠ const.
Например, статическая характеристика насыщенного генератора постоянного тока представлена на рис.16. Обычно нелинейная характеристика не может быть выражена какой-либо математической зависимостью и ее приходится задавать таблично или графически.
Зная статические характеристики отдельных звеньев, можно построить статическую характеристику САУ (рис.17, 18). Если все звенья САУ линейные, то САУ имеет линейную статическую характеристику и называется линейной. Если хотя бы одно звено нелинейное, то САУ нелинейная.
Звенья, для которых можно задать статическую характеристику в виде жесткой функциональной зависимости выходной величины от входной, называются статическими. Если такая связь отсутствует и каждому значению входной величины соответствует множество значений выходной величины, то такое звено называется астатическим. Изображать его статическую характеристику бессмысленно. Примером астатического звена может служить двигатель, входной величиной которого является напряжение U, а выходной - угол поворота вала
Передаточная функция В ТАУ часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператора p = d/dt так, что, dy/dt = py, а pn = dn/dtn. Это лишь другое обозначение операции дифференцирования. Обратная дифференцированию операция интегрирования записывается как 1/p. В операторной форме исходное дифференциальное уравнение aoy(n) + a1y(n-1) +... + an - 1y’ + any = bo x(m) +... + bm – 1 x’ + bm x записывается как алгебраическое: ao pn y + a1 pn-1 y +... + an y = bo pm x + b1 pm-1 x +... + bm x или (ao p n + a1 pn-1 +... + an) y = (bo pm + b1 pm-1 +... + bm)x Не надо путать эту форму записи с операционным исчислением хотя бы потому, что здесь используются непосредственно функции времени y(t), x(t) (оригиналы), а не их изображения Y(p), X(p), получаемые из оригиналов по формуле преобразования Лапласа. Вместе с тем при нулевых начальных условиях с точностью до обозначений записи действительно очень похожи. Это сходство лежит в природе дифференциальных уравнений. Поэтому некоторые правила операционного исчисления применимы к операторной форме записи уравнения динамики. Так оператор p можно рассматривать в качестве сомножителя без права перестановки, то есть py
Дифференциальный оператор W(p) называют передаточной функцией. Она определяет отношение выходной величины звена к входной в каждый момент времени: W(p) = y(t)/x(t), поэтому ее еще называют динамическим коэффициентом усиления. В установившемся режиме d/dt = 0, то есть p = 0, поэтому передаточная функция превращается в коэффициент передачи звена K = bm/an. Знаменатель передаточной функции D(p) = aopn + a1pn - 1 + a2pn - 2 +... + an называют характеристическим полиномом. Его корни, то есть значения p, при которых знаменатель D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами передаточной функции. Числитель передаточной функции K(p) = bopm + b1pm - 1+... + bm называют операторным коэффициентом передачи. Его корни, при которых K(p) = 0 и W(p) = 0, называются нулями передаточной функции. Звено САУ с известной передаточной функцией называется динамическим звеном. Оно изображается прямоугольником, внутри которого записывается выражение передаточной функции. То есть это обычное функциональное звено, функция которого задана математической зависимостью выходной величины от входной в динамическом режиме. Для звена с двумя входами и одним выходом должны быть записаны две передаточные функции по каждому из входов. Передаточная функция является основной характеристикой звена в динамическом режиме, из которой можно получить все остальные характеристики. Она определяется только параметрами системы и не зависит от входных и выходных величин. Например, одним из динамических звеньев является интегратор. Его передаточная функция Wи(p) = 1/p. Схема САУ, составленная из динамических звеньев, называется структурной. Дифференцирующее звено Различают идеальное и реальное дифференцирующие звенья. Уравнение динамики идеального звена: Идеальное дифференцирующее звено реализовать невозможно, так как величина всплеска выходной величины при подаче на вход единичного ступенчатого воздействия всегда ограничена. На практике используют реальные дифференцирующие звенья, осуществляющие приближенное дифференцирование входного сигнала. Его уравнение: T p y + y = k T p x, или (T p + 1)y = k T p x Передаточная функция: При малых Т звено можно рассматривать как идеальное дифференцирующее звено. Переходную характеристики можно вывести с помощью формулы Хевисайда:
здесь p1 = - 1/T - корень характеристического уравнения D(p) = Tp + 1 = 0; кроме того, D’(p1) = T. При подаче на вход единичного ступенчатого воздействия выходная величина оказывается ограничена по величине и растянута во времени (рис.47). По переходной характеристике, имеющей вид экспоненты, можно определить передаточный коэффициент k и постоянную времени Т. Примерами таких звеньев могут являться четырехполюсник из сопротивления и емкости или сопротивления и индуктивности, демпфер и т.п. Дифференцирующие звенья являются главным средством, применяемым для улучшения динамических свойств САУ.
Кроме рассмотренных имеется еще ряд звеньев, на которых подробно останавливаться не будем. К ним можно отнести идеальное форсирующее звено (W(p) = Tp + 1, практически не реализуемо), реальное форсирующее звено (W(p) =  , при T1 >> T2), запаздывающее звено (W(p) = e - pT), воспроизводящее входное воздействие с запаздыванием по времени и другие. , при T1 >> T2), запаздывающее звено (W(p) = e - pT), воспроизводящее входное воздействие с запаздыванием по времени и другие.
Контрольные вопросы
Безынерционное звено Передаточная функция: W(p) = k. АФЧХ: W(j ВЧХ: P( МЧХ: Q( АЧХ: A( ФЧХ: ЛАЧХ: L(
Некоторые ЧХ показаны на рис.50. Звено пропускает все частоты одинаково c увеличением амплитуды в k раз и без сдвига по фазе.
Интегрирующее звено
Передаточная функция: W(p) = k/p. Рассмотрим частный случай, когда k = 1, то есть W(p) = 1/p. АФЧХ: ВЧХ: P( МЧХ: Q( АЧХ: A( ФЧХ: ЛАЧХ: L( ЧХ показаны на рис.51. Все частоты звено пропускает с запаздыванием по фазе на 90о. Амплитуда выходного сигнала увеличивается при уменьшении частоты, и уменьшается до нуля при росте частоты (звено "заваливает" высокие частоты). ЛАЧХ представляет собой прямую, про
ходящую через точку L(  ) = 0 при ) = 0 при  = 1. При увеличении частоты на декаду ордината уменьшается на 20lg10 = 20дб, то есть наклон ЛАЧХ равен - 20 дб/дек (децибел на декаду). = 1. При увеличении частоты на декаду ордината уменьшается на 20lg10 = 20дб, то есть наклон ЛАЧХ равен - 20 дб/дек (децибел на декаду).
Апериодическое звено При k = 1 получаем следующие выражения ЧХ:
;
Здесь A1 и A2 - амплитуды числителя и знаменателя ЛФЧХ; ЛФЧХ: L( ЧХ показаны на рис.52.
АФЧХ есть полуокружность радиусом 1/2 с центром в точке P = 1/2. При построении асимптотической ЛАЧХ считают, что при ЛФЧХ асимптотически стремится к нулю при уменьшении w до нуля (чем меньше частота, тем меньше искажения сигнала по фазе) и к -
Вопросы
Законы регулирования Пусть задана какая-то САР (рис.59).
Законом регулирования называется математическая зависимость, в соответствии с которой
управляющее воздействие на объект вырабатывалось бы безынерционным регулятором.
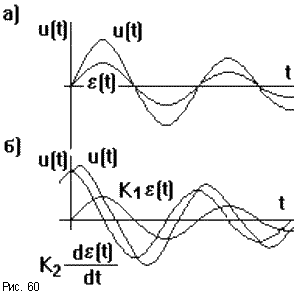
Простейшим из них является пропорциональный закон регулирования, при котором u(t) = Ke(t) (рис.60а), где u(t) - это управляющее воздействие, формируемое регулятором, e(t) - отклонение регулируемой величины от требуемого значения, K - коэффициент пропорциональности регулятора Р.
То есть для создания управляющего воздействия необходимо наличие ошибки регулирования и чтобы величина этой ошибки была пропорциональна возмущающему воздействию f(t). Другими словами САУ в целом должна быть статической. Такие регуляторы называют П-регуляторами. Так как при воздействии возмущения на объект управления отклонение регулируемой величины от требуемого значения происходит с конечной скоростью (рис.60б), то в начальный момент на вход регулятора подается очень малая величина e, вызывая при этом слабые управляющие воздействия u. Для повышения быстродействия системы желательно форсировать процесс управления. Для этого в регулятор вводят звенья, формирующие на выходе сигнал, пропорциональный производной от входной величины, то есть дифференцирующие или форсирующие звенья. Такой закон регулирования называется пропорционально - дифференциальным: u(t) = K1e(t) + K2 В соответствии с ним работают ПД-регуляторы. Чем быстрее нарастает отклонение регулируемой величины от требуемого значения, тем интенсивнее работает ПД-регулятор, что препятствует дальнейшему нарастанию данного отклонения. Кроме того при увеличении отклонения (de(t)/dt > 0) управляющий сигнал u будет больше, чем при уменьшении (de(t)/dt < 0), что также играет положительную роль, снижая колебательность процеса управления. Добавление в регулятор двух дифференцирующих звеньев позволяет формировать управляющее воздействие по второй производной отклонения e, такой регулятор называется ПДД-регулятором. Интегральный закон регулирования реализуется И-регулятором, его формулировка:
Этот регулятор наращивает управляющее воздействие до тех пор пока управляемая величина отличается от требуемого значения, то есть пока e(t) И-регулятор обеспечивает астатическое регулирование. При малых e управляющее воздействие изменяется с малой скоростью, поэтому данный регулятор очень инерционный. Чтобы увеличить быстродействие обычно последовательно с ним включают усилитель, это дает пропорционально-интегральный закон регулирования (ПИ-регулятор), его формула:
Первое слагаемое обеспечивает быстродействие, второе - астатичность, то есть точность регулирования. Еще большее быстродействие обеспечивается при добавлении слагаемого, пропорционального производной от отклонения управляемой величины de/dt, такой закон регулирования обеспечивается ПИД-регулятором, его формула:
. Контрольные вопросы
Критерий Рауса
Раус предложил критерий устойчивости САУ в виде алгоритма, по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения: 1. в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания; 2. во второй строке - с нечетными; 3. остальные элементы таблицы определяется по формуле: ck,i = ck+ 1,i - 2 - ri 4. Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.
Критерий Рауса: для того, чтобы САУ была устойчива, необходимо и
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-15; просмотров: 454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.105.110 (0.016 с.) |













 , величина которого при U = const может принимать любые значения. Выходная величина астатического звена даже в установившемся режиме является функцией времени.
, величина которого при U = const может принимать любые значения. Выходная величина астатического звена даже в установившемся режиме является функцией времени. yp. Его можно выносить за скобки и т.п. Поэтому уравнение динамики можно записать также в виде:
yp. Его можно выносить за скобки и т.п. Поэтому уравнение динамики можно записать также в виде:
 , или y = k p x. Здесь выходная величина пропорциональна скорости изменения входной величины. Передаточная функция: W(p) = kp. При k = 1 звено осуществляет чистое дифференцирование W(p) = p. Переходная характеристика: h(t) = k
, или y = k p x. Здесь выходная величина пропорциональна скорости изменения входной величины. Передаточная функция: W(p) = kp. При k = 1 звено осуществляет чистое дифференцирование W(p) = p. Переходная характеристика: h(t) = k  1’(t) = d(t).
1’(t) = d(t). .
.
 ,
,
 (
(

 /2.
/2.
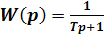 ;
;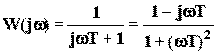
 ;
; ;
;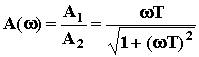 ;
;
 - 10lg1 = 0.. При
- 10lg1 = 0.. При 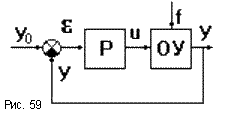
 .
. .
.
 .
. 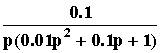 .
.  3 - номер строки, k - номер столбца.
3 - номер строки, k - номер столбца.


