
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 10. Статистический анализ взаимосвязи явлений в правовой сфереСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Роль и задачи статистического анализа социально-правовых явлений. 2. Закон больших чисел. 3. Случайное событие и случайная величина. 4. Частота и вероятность случайного события. 5. Центральная предельная теорема. 6. Законы распределения случайной величины. 7. Особенности нормального распределения. 8. Виды взаимосвязи явлений и факторов: статистическая и динамическая закономерность. 9. Функционально-детерминированная и стохастически-детерминированная (корреляционная) связи. 10. Задача корреляционного анализа явлений в правовой сфере. 11. Методы выявления и оценки статистических связей. 12. Метод параллельных рядов. 13. Понятие и виды корреляционной связи. 14. Показатели корреляции. 15. Определение тесноты связи качественных признаков. 16. Коэффициент контингенции. 17. Коэффициенты взаимной сопряженности Чупрова и Пирсона. 18. Определение тесноты связи количественных признаков. 19. Коэффициент парной линейной корреляции Пирсона. 20. Регрессионный анализ. 21. Линейное уравнение парной регрессии и расчет его параметров. Роль и задачи статистического анализа социально-правовых явлений. Статистический анализ является третьим, завершающим этапом любого статистического исследования и заключается в изучении обобщенных количественных данных о различных аспектах рассматриваемых явлений, определении, сопоставлении и истолковании статистико-математических характеристик этих данных. Статистический анализ социально-правовых явлений может быть направлен на решение как частных, так и общих задач. При решении частных задач целью анализа является выяснение реального состояния явления и его составляющих в конкретных условиях места и времени, роли каждого из влияющих факторов, определение динамики, причин данного состояния явления и прогнозов его развития. При решении общих задач целью анализа является получение полной и всесторонней картины развития изучаемого явления в целом, во взаимосвязи со смежными явлениями, выработка научных и практических выводов и рекомендаций по совершенствованию функционирования государственных и общественных механизмов в изучаемой сфере общественных отношений. Для понимания сущности статистических закономерностей, раскрывающих связи между разнородными явлениями, освоения методов количественной оценки этих связей, необходимо предварительно рассмотреть понятия случайных событий, случайных величин и вероятности. Случайные события и величины. Понятие вероятности. Наблюдаемое событие (факт) является случайным, если оно в процессе наблюдения может наступить, а может не наступить. Для идентификации и математического описания случайных событий и величин им принято присваивать имена, состоящие обычно из одной буквы (реже используются имена из нескольких букв). Например, буквой «А», «В» и т.д. Наблюдаемая величина является случайной, если она в процессе наблюдения может принять любое значение из определенного интервала (перечня). Важнейшим элементом как практических наблюдений за случайными событиями и величинами, так и их математического моделирования является фиксация наблюдателем исхода конкретного наблюдения или результата очередного испытания. Благоприятным исходом наблюдения называется появление изучаемого факта или тот случай, когда возможное (ожидаемое) событие произошло. После проведения серии наблюдений за некоторым случайным событием и фиксации их результатов, можно определить количественную характеристику того, как часто, в целом, появлялся благоприятный исход, называемую частотой появления случайного события. Частота появления случайного события А – это отношение числа благоприятных исходов к общему числу наблюдений. f(А) = В / N, где f(A) – частота появления случайного события А; В – количество благоприятных исходов; N – общее количество наблюдений. Так как В всегда меньше или равно N, то f(A) всегда принимает значения в диапазоне от 0 до 1. В теории вероятностей это фундаментальное для данной науки понятие определено в центральной предельной теореме, которая может быть сформулирована следующим образом: Вероятность события – это предел, к которому стремится частота появления события при стремлении числа наблюдений к бесконечности. Вероятность случайного события А обычно обозначается как Р(А). Выявление и оценка статистических связей в правовой сфере Выявление и количественная оценка причинно-следственных связей, определение степени влияния факторных признаков на результатные является одной из важнейших задач статистического анализа. Особое место в правовой статистике занимает изучение связей между криминогенными факторами и преступным поведением или факторами, снижающими вероятность противоправных действий и фактическим уровнем преступности. Корреляционный анализ. Важнейшим частным случаем статистической связи является корреляционная связь*, которая состоит в том, что в зависимости от изменения значения факторного признака меняется средняя величина значений результатного признака. Для числового выражения тесноты (силы) корреляционной статистической связи применяются различные показатели (коэффициенты) корреляции. Указанные показатели (коэффициенты) корреляции (обозначим их обобщённо – ПК) могут принимать значения от -1 до +1. При этом чем больше абсолютная величина ПК, тем сильнее связь. Знак ПК при изучении взаимосвязи между количественными признаками показывает направление этой связи. При изучении взаимосвязи между качественными (атрибутивными) признаками знак ПК не имеет универсальной интерпретации. Определение тесноты связи качественных (атрибутивных) признаков. Наиболее простым случаем связи качественных признаков является связь между двумя альтернативными признаками. Тесноту связи таких признаков можно определить с помощью коэффициента контингенции:
К - коэффициент контингенции; а, b, с, d – частоты всех возможных сочетаний вариантов изучаемых признаков в статистической совокупности. Для получения значений частот предварительно создаётся частотная таблица (Таблица 10). Таблица 10 Общий вид частотной таблицы для двух альтернативных признаков
Определение тесноты связи количественных признаков. Одним из наиболее простых и распространённых показателей тесноты связи двух количественных признаков X и Y является коэффициент парной линейной корреляции Пирсона, рассчитываемый по формуле:
R – коэффициент корреляции Пирсона; n – количество эмпирических значений признака X и соответствующих им средних значений признака Y; i – текущий номер пары значений х, у; xi – значение с номером i факторного признака; хср – среднее значение факторного признака; yi – среднее значение с номером i результатного признака; Уср._ усредненное значение всех наблюдаемых средних значений результатного признака. Регрессионный анализ. Регрессионный анализ, также как и корреляционный позволяет выявлять наличие и направление связи между количественными признаками, судить о её силе. В практике правовой статистики для регрессионного анализа в большинстве случаев применяется линейное уравнение парной регрессии: yti = а + b xi, где, (4) i – текущий номер пары значений х, у; yti – теоретическое среднее значение результатного признака, соответствующее значению с номером i факторного признака; xi – значение с номером i факторного признака; а - постоянный параметр уравнения, отражающий значение yti при xi = 0 (при наличии нулевого значения в поле допустимых значений факторного признака). При отсутствии нулевого значения в поле допустимых значений факторного признака параметр а не интерпретируется. b – коэффициент регрессии (постоянный параметр уравнения, показывающий на какую величину изменяется среднее значение результатного признака при изменении факторного признака на 1 единицу в единицах измерения этого признака). Знак указывает на направление связи («+» означает прямую связь, «-» означает обратную связь). Формулы для расчёта параметров линейного уравнения регрессии, выводимые на основе метода наименьших квадратов, имеют следующий вид:
n – количество эмпирических значений признака X и соответствующих им средних значений признака Y; yi – среднее эмпирическое значение с номером i результатного признака. Кроме того, используя формулу (4), можно вычислить теоретические (ожидаемые) значения результатного признака для фактически отсутствующих в составе исходных данных значений х, получив тем самым определённый прогноз состояния изучаемого явления.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 758; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.97.1 (0.009 с.) |

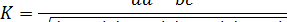
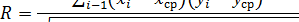
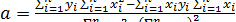
 где
где


