
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. История развития статистики и формирования правовой статистикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Тема 4. Статистическая информация и методы ее представления 1. Законодательное определение понятий «Информация», «Документированная информация», «Официальная статистическая информация». 2. Понятие и особенности статистической таблицы. 3. Обязательные реквизиты и структура статистической таблицы (строки, графы, графоклетки, статистические подлежащее и сказуемое). 4. Разработка статистической таблицы. 5. Последовательность создания макета таблицы. 6. Виды статистических таблиц. 7. Понятие и элементы статистического графика. 8. Виды статистических графиков. Тема 5. Основные категории и понятия статистической науки 1. Общефилософские категории («качество» и «количество», «сущность» и «явление», «необходимость» и «случайность»), используемые при описании статистической методологии. 2. Понятия статистической совокупности и единицы совокупности. 3. Понятие статистического признака. 4. Варианты статистических признаков. 5. Виды признаков. 6. Понятие статистического показателя. 7. Виды показателей. 8. Понятие вариации. 9. Цель определения показателей вариации. Качество – философская категория, выражающая совокупность существенных признаков, особенностей и свойств, которые отличают один предмет или явление от других и придают ему определённость. Качество предмета или явления, как правило, не сводится к отдельным его свойствам. Оно связано с предметом как целым, охватывает его полностью и неотделимо от него. Поэтому понятие качества связывается с бытием предмета. Предмет не может, оставаясь самим собой, потерять свое качество. Например, переход в новое качество Количество – категория, выражающая внешнее, формальное взаимоотношение предметов или их частей, а также свойств, связей: их величину, число, степень проявления того или иного свойства. Сущность – смысл данной вещи, то, что она есть сама по себе, в отличие от всех других вещей и в отличие от изменчивых, под влиянием тех или иных обстоятельств, состояний вещи. Явление – вообще всё, что чувственно воспринимаемо, особенно бросающееся в каком-то отношении в глаза (например, какое-либо явление природы). Необходимость – характеристика явления, однозначно определённого некоторой областью действительности, предсказуемого в рамках знания о ней. Необходимость противопоставляют случайности. Случайность – философская категория, выражающая один из предельных видов (классов) взаимосвязей и взаимоотношений в мире, характеризующийся отсутствием прямых закономерных связей в поведении и функционировании объектов и систем. Предметом исследования статистики является количественная сторона массовых общественных явлений в неразрывной связи с их качественной стороной или их содержанием, а также количественное выражение закономерностей общественного развития в конкретных условиях места и времени. Именно потому, что статистика изучает массовые явления, она позволяет выявить и измерить закономерности развития этих процессов, а также взаимосвязь между ними, т.к. закономерности общественной жизни в полной мере проявляются лишь в массовом явлении. В каждом отдельном явлении есть необходимое (то, что присуще явлениям данного вида) и случайное (индивидуальное – то, что присуще только конкретному отдельному явлению). Причем необходимое проявляется в единстве со случайным. Закономерности, в которых необходимость неразрывно связана в каждом отдельном явлении со случайностью, и только во множестве явлений проявляет себя как закон, называют статистическими закономерностями. Рассмотрим основные понятия, используемые в статистике. Статистическая совокупность – совокупность социально-экономических объектов или явлений общественной жизни, объединенных некоей качественной основой, общей связью, но отличающихся друг от друга отдельными признаками. Совокупности могут быть: - однородными, если один или несколько изучаемых существенных признаков ее объектов являются общими для всех единиц. Совокупность оказывается однородной именно с точки зрения этих признаков. - разнородными, в которую входят явления разного типа. Совокупность может быть однородна в одном отношении и разнородна в другом. В каждом отдельном случае однородность совокупности устанавливается путем проведения качественного анализа, выяснения содержания изучаемого общественного явления.
Единица совокупности – первичный элемент статистической совокупности, являющийся носителем признаков, подлежащих регистрации, и основой ведущегося при обследовании счета. Признак – качественная особенность единицы совокупности. По характеру отображения свойств единиц изучаемой совокупности признаки делятся на две основные группы: - признаки, имеющие непосредственное количественное выражение, например возраст, стаж работы, средний заработок и т. д. Они могут быть дискретными и непрерывными; - признаки, не имеющие непосредственного количественного выражения. В этом случае отдельные единицы совокупности различаются своим содержанием (например, профессии – характером труда: учитель, водитель и т. д.). Такие признаки обычно называют атрибутивными (в философии «атрибут» – неотъемлемое свойство предмета). В случае, когда имеются противоположные по значению варианты признака, говорят об альтернативном признаке (да, нет). Например, продукция может быть годной или бракованной (негодной) и т. д. Особенностью статистического исследования является то, что в нем изучаются только варьирующие признаки, т. е. признаки, принимающие различные значения (для атрибутивных, альтернативных признаков) или имеющие различные количественные уровни у отдельных единиц совокупности. Вариация – это изменение величины либо значения признака при переходе от одной единицы совокупности к другой. Статистический показатель – понятие, отображающее количественные характеристики соотношения признаков общественных явлений. Каждый показатель формируется под действием ряда причин, часть из которых носит индивидуальный (случайный) характер. В обобщающих статистических показателях отчетливо проявляются следствия, обусловленные общими причинами и сглаживаются, обусловленные индивидуальными. В этом проявляется действие закона больших чисел. Законом больших чисел называется свойство статистических закономерностей проявляться в массовых числах. Система статистических показателей – совокупность статистических показателей, отражающая взаимосвязи, которые объективно существуют между явлениями. Система статистических показателей охватывает все стороны жизни общества на различных уровнях: страны и региона (макроуровень), предприятий, фирм, объединений, семей и домохозяйств и т.д. (микроуровень). Совокупность приемов, пользуясь которыми статистика исследует свой предмет, составляет метод статистики. Можно выделить три группы статистических методов: 1) метод массовых наблюдений. Известно, что первый этап всякого статистического исследования – это статистическое наблюдение. Оно заключается в сборе первичного статистического материала, в научно организованной регистрации всех существенных фактов, относящихся к рассматриваемому объекту; 2) метод группировок, суть которого заключается в том, чтобы все собранные в результате массового статистического наблюдения факты подвергнуть систематизации и классификации (второй этап статистического исследования); 3) метод обобщающих показателей, позволяющий характеризовать изучаемые явления и процессы при помощи статистических величин — абсолютных, относительных и средних с целью выявить взаимосвязи и масштабы явлений, закономерности их развития, дать прогнозные оценки.
Тема 8. Ряды динамики 1. Ряды динамики абсолютных, относительных и средних величин. 2. Аддитивная и мультипликативная модели рядов динамики. 3. Тренд, сезонный и циклический компоненты рядов динамики. 4. Понятие временного лага. 5. Сопоставимость данных в рядах динамики. 6. Смыкание рядов динамики. 7. Абсолютный прирост, темп роста, темп прироста. 8. Базисная, цепная и средняя формы показателей динамики. 9. Сглаживание рядов динамики. 10. Метод укрупнения интервалов. 11. Аналитическое сглаживание рядов динамики методом наименьших квадратов. 12. Экстраполяция динамического ряда.
Понятие, виды и назначение статистических рядов динамики Ряд динамики (или временной ряд, динамический ряд) – это расположенные в хронологическом порядке числовые значения, отражающие развитие изучаемого явления за определённый период времени. В структуру ряда динамики входят два основных элемента: 1. моменты или интервалы времени (tn); 2. уровни динамического ряда (Yn), представляющие собой числовые значения, количественно характеризующие изучаемое явление в указанные моменты (или интервалы) времени. Общее число моментов (интервалов) времени, отражённых в ряду динамики или время от первого до последнего называется длиной динамического ряда. Ряды динамики классифицируют по нескольким различным основаниям. По способу указания времени различают интервальные и моментные динамические ряды. В интервальных динамических рядах временной элемент ряда указывается в виде определённого интервала, промежутка времени, отображаемого на временной шкале в виде отрезка, имеющего чётко обозначенные границы. При этом каждый уровень такого ряда отражает общее значение изучаемого показателя за соответствующий интервал времени, получаемое путём суммирования значений этого показателя, зарегистрированных за все более мелкие отрезки времени, входящие в данный интервал. В моментных динамических рядах временной элемент ряда указывается в виде определённого момента, одной точки на шкале времени. При этом, каждый уровень такого ряда отражает значение изучаемого показателя, зафиксированное на указанный момент (дату, час и т.д.). При внешней схожести моментных и интервальных динамических рядов принципиальная разница между ними заключается в том, что в состав разных уровней одного моментного ряда могут входить одни и те же единицы изучаемой совокупности, а в интервальном ряду - не могут. Из сказанного следует, что сложение уровней допустимо только для интервальных динамических рядов, в которых эти уровни выражены в абсолютных величинах. Для всех других видов интервальных рядов и для всех моментных рядов сложение уровней одного ряда недопустимо. По расстоянию между датами или интервалам времени выделяют полные и неполные ряды. В полных интервальных рядах динамики все интервалы равны друг другу по продолжительности, а в полных моментных рядах даты (моменты) регистрации также отстоят друг от друга на равные промежутки времени. В неполных рядах динамики принцип равенства интервалов не соблюдается. По количеству одновременно изучаемых показателей - выделяют изолированные и комплексные (многомерные) ряды. При этом в изолированном ряду динамики всегда представлено развитие во времени одного показателя, а в комплексном ряду в хронологической последовательности рассматривается система из двух и более связанных между собой показателей. Компоненты уровней и назначение рядов динамики. Наблюдаемая изменчивость уровней рядов динамики объясняется одновременным действием двух составляющих: детерминированной (закономерной) и случайной. Детерминированная (закономерная) составляющая, в свою очередь, состоит из следующих компонентов: тренд (TRi), сезонный компонент (Si) и циклический компонент (Ci). Di = TRi + Si + Ci Тренд – это не циклический, плавно изменяющийся компонент уровней ряда динамики, показывающий основную тенденцию развития изучаемого явления под воздействием существенных устойчивых факторов в течение длительного времени. Структура рядов динамики тесно связана с их назначением. Ряды динамики используются для анализа закономерностей в изучаемых явлениях по следующим основным направлениям: 1. характеристика уровней развития явления во времени; 2. измерение динамики явления посредством системы специальных статистических показателей (абсолютный прирост, темп роста, темп прироста); 3. выявление и количественная оценка основной тенденции развития явления (тренда); 4. изучение сезонных и циклических колебаний регистрируемых показателей; 5. прогнозирование развития изучаемого явления.
Анализ скорости (интенсивности) динамики изучаемых показателей Визуальное восприятие динамического ряда позволяет количественно оценить уровни изучаемого явления в определённые интервалы (моменты) времени, констатировать наличие изменчивости этих уровней, и, в некоторых случаях, выявить общее направление динамики (рост или снижение значений показателя), однако, определить скорость (интенсивность) происходивших изменений можно лишь рассчитав специальные показатели динамики. Наиболее распространёнными показателями динамики являются: абсолютный прирост, темп роста, темп прироста, каждый из которых имеет три формы - базисную, цепную и среднюю.
Базисный абсолютный прирострассчитывается по формуле: ΔБi = Yi – Y1, где i - текущий номер уровня в ряду, начиная со второго; Yi – текущий уровень ряда; Y1 – начальный уровень ряда;
Цепной абсолютный прирост рассчитывается по формуле: ΔЦ i = Yi – Yi-1, где i – текущий номер уровня в ряду; Yi – текущий уровень ряда; Yi-1 – уровень ряда, предшествующий текущему;
Средний абсолютный прирост рассчитывается по формуле: ΔСР = ΣΔЦi / (n – 1), где i – текущий номер уровня в ряду, начиная со второго; ΔЦi – цепной абсолютный прирост для текущего уровня ряда; n – количество уровней в ряду (длина ряда).
Данный показатель можно рассчитать и по более простой формуле: ΔСР = (Yn – Y1)/ (n – 1), где Yn – последний (конечный) уровень ряда; Y1 – первый (начальный) уровень ряда, n – количество уровней в ряду (длина ряда);
Сглаживание рядов динамики Как уже отмечалось, среди задач, решаемых с использованием рядов динамики, одной из важнейших является задача выявления тренда. Процесс нивелирования слишком сильных колебаний уровней ряда с целью выявления тренда называется сглаживанием динамического ряда. Различают два вида сглаживания: эмпирическое (механическое) и аналитическое, которые, в свою очередь, могут реализовываться различными методами. Наиболее распространённым методом эмпирического сглаживания является метод скользящей средней, который заключается в замене уровней сглаживаемого ряда на средние значения уровней за несколько смежных интервалов. Построение сглаженного ряда осуществляется следующим образом. Определённое количество интервалов (в случае интервального ряда) или периодов времени между фиксированными моментами (в случае моментного ряда), начиная с первого, объединяются в укрупнённый интервал сглаживания. Количество уровней, входящих в интервал сглаживания, называется порядком скользящей средней (К). Вычисляется средняя арифметическая уровней, входящих в интервал сглаживания (сумма всех уровней, вошедших в этот интервал, делённая на К) и полученное значение заносится в создаваемый сглаженный ряд качестве первого уровня. Затем интервал сглаживания сдвигается и в качестве его начального уровня выбирается второй уровень исходного ряда при неизменном значении К (т.е. интервал сглаживания смещается по исходному ряду на один уровень от его начала к концу) и по новому составу интервала сглаживания вновь вычисляется средняя арифметическая входящих в него уровней, значение которой заносится в создаваемый сглаженный ряд качестве второго уровня. Таким образом, интервал сглаживания как бы скользит по исходному ряду динамики, и эта процедура повторяется до тех пор, пока не достигает конечного уровня этого исходного ряда. Чтобы увеличить степень сглаженности ряда можно увеличить величину порядка скользящей средней (К), но следует иметь в виду, что при этом уменьшится и длина ряда (на К – 1 уровней), а значит и его информативность. В отличие от эмпирического сглаживания сущность всех методов аналитического сглаживания состоит в определении параметров математической модели рассматриваемого явления (т.е. функции, описывающей изменение изучаемого показателя) и использовании этой модели для вычисления теоретических (сглаженных) уровней показателя как в пределах фактически наблюдаемого временного ряда, так и за его пределами. Конкретный метод аналитического сглаживания определяется тем, какой из следующих наиболее применимых видов функции выбран: - линейная: Yt = а + b . t; - показательная: Yt = а . bt; - параболическая: Yt = a + b . t +c . t2 Наиболее применяемым методом аналитического сглаживания является сглаживание по прямой методом наименьших квадратов, при котором для линейной функции вычисляются такие значения параметров (а и b), при которых выполняется следующее условие:
n – длина ряда (количество уровней); i – текущий номер уровня; YFi – уровни фактического (исходного) ряда; YRi – уровни расчётного (теоретического) ряда, определяемые из уравнения: YRi = а + b . ti, где (2) а – уровень ряда на момент времени t = 0; b – коэффициент расчётной скорости ряда; ti – условный номер интервала (момента) времени. Поскольку значения ti всегда известны, то для вычисления теоретических уровней остаётся определить значения параметров а и b. Для упрощения вычисления данных параметров необходимо заменить реальные номера интервалов (моментов) времени исходного ряда на условные номера таким образом, чтобы сумма этих номеров стала равной нулю. Осуществляется эта замена следующим образом: если длина исходного ряда (количество имеющихся уровней) выражается нечётным числом, то срединному уровню присваивается номер 0, предыдущий уровень получает отрицательный условный номер -1, предшествующий ему уровень – условный номер -2 и т.д. Уровни, следующие за срединным в сторону увеличения номеров, получают положительные условные номера +1, +2 и т.д. Если же длина исходного ряда – число чётное, то уровни первой половины ряда получают отрицательные нечётные условные номера (считая от последнего уровня этой половины к первому) -1, -3, -5 и т.д., а уровни второй половины ряда получают положительные нечётные условные номера (считая от первого уровня этой половины к последнему) +1, +3, +5 и т.д. После выполнения указанной замены параметры а и b уравнения (2) могут быть определены по следующим упрощённым формулам:
tui - условные номера интервалов (моментов). Таким образом, параметр а представляет собой средний уровень исходного ряда, а параметр b - коэффициент скорости динамики расчётного (теоретического) ряда. Заменив в уравнении (2) параметры а и b их вычисленными числовыми значениями, мы получим простую формулу, на основе которой для каждого условного номера интервала рассчитывается свой теоретический уровень. Последовательность этих расчётных уровней, соотнесённых с имеющимися в исходном ряду интервалами (моментам) времени и будет представлять собой аналитически сглаженный ряд динамики. Если последовательность условных номеров интервалов продолжить за временные пределы исходного ряда (в будущее), то вычисление для них по той же формуле теоретических уровней будет являться экстраполяцией исходного ряда, а сами эти уровни будут представлять собой статистический прогноз значения изучаемого показателя на предстоящие периоды.
Тема 1. История развития статистики и формирования правовой статистики 1. Этимология слова «статистика». 2. Государствоведческие работы Аристотеля как пример зарождения статистических описаний в Древнем мире. 3. Три школы статистической науки. 4. Развитие в России системы государственной статистики. 5. В. Н. Татищев и М. В. Ломоносов как авторы первых в России научно-методических работ по статистике. 6. Появление в России системы губернских статистических органов и их задачи. 7. Выделение и развитие правового раздела статистики. 8. Роль А. Н. Радищева как родоначальника правового («морального») раздела статистики. 9. Причины развития правовой статистики под именем «моральная». 10. Этапы развития земской статистики. 11. Особенности советского периода развития статистики. 12. Направление реформирования российской государственной статистики в период перехода к рыночной экономике. В современном обществе важную роль в механизме управления экономикой выполняет статистика. Независимо от уровня и стадии экономического развития, характера политической системы, статистика на протяжении сотен лет своего существования всегда выступала как необходимый и эффективный инструмент государственного управления и одновременно как наука, исследующая количественную сторону массовых явлений. Особенность статистики заключается в том, что статистические данные сообщаются в количественной форме, т.е. статистика говорит языком цифр, отображающих общественную жизнь во всем многообразии ее проявлений. При этом статистику прежде всего интересуют те выводы, которые можно сделать на основе анализа надлежащим образом собранных и обработанных цифровых данных. Выполняя самые разнообразные функции сбора, систематизации и анализа сведений, характеризующих экономическое и социальное развитие общества, она всегда играла роль главного поставщика факторов для управленческих, научно-исследовательских и прикладных практических нужд различного рода структур, организаций и населения. Слово «статистика» многолико, многозначно и согласно одному из статистических терминов многомерно. В настоящее время насчитывается около тысячи определений статистики. Дать определение статистики как науке пытались философы, математики, экономисты, социологи, государственные деятели и, конечно, сами статистики. Сам термин «статистика» произошел от латинского слова «статус», что означает «определенное положение вещей». Термин «статистика» употребляется в различных значениях. Под статистикой понимается практическая деятельность по сбору, накоплению, обработке и анализу цифровых данных, характеризующих население, экономику, культуру, образование и другие явления в жизни общества. Употреблялся он первоначально в значении слова «государствоведение». Статистикой также называют особую науку, т. е. отрасль знаний, изучающую явления в жизни общества с их количественной стороны. Как учебная дисциплина статистика составляет важный блок учебного плана подготовки коммерсантов, менеджеров, экономистов высшей квалификации. Статистика как практическая деятельность людей зародилась в глубокой древности. Ее возникновение и развитие были обусловлены общественными потребностями: подсчет населения, скота, учет земельных угодий, имущества и т.д. Наиболее ранние сведения о таких работах в Китае относятся к V веку II тыс. до н.э. В Древнем Риме проводились учеты свободных граждан и их имущества. Учёт осуществлялся по полу и возрасту, собирались сведения о состоянии промышленности и сельского хозяйства. В античном мире учитывали родившихся; в специальные списки вносились юноши, достигшие возраста военнообязанных (18 лет), а также 20 лет (возраст полноправных граждан). Составлялись земельные списки (кадастры), в которые включались сведения о строениях, рабах, скоте, инвентаре, доходах. Греческий философ Аристотель ещё за триста лет до нашей эры составил описание 157 городов государств. В 1061 г. в Англии проведена всеобщая перепись населения, в ходе которой обследовано 240 тысяч дворов. Монгольские ханы проводили переписи в середине XIIIв. для взимания дани с захваченных русских земель. На Руси первыми статистическими источниками были летописи, в которых упоминается о сборе различной информации в IX-XIвв.: возникновении и развитии городских поселений, расположенных на водных путях, о наличии в них храмов, церквей, монастырей, жилых строений. В XVIв. в Венеции, Голландии появляются сборники, характеризующие политическое устройство, население, основные занятия, производимую продукцию в странах, с которыми устанавливалась торговля. В процессе практических статистических работ начали складываться определённые правила сбора и обработки данных, приёмы анализа информации. Появляется необходимость теоретического научного осмысления накопленной практики. Начали складываться и исторические черты познания массовых явлений и формы их количественного измерения. Каждый этап в этом движении есть современность, и каждая современность есть отрезок по пути исторического развития. Каждая отрасль научного знания и практической деятельности имеет свою историю, т. е. процесс обогащения общества этими знаниями, их становления. Знакомство с историей - ключ познания современности. Без знания прошедшего нет вдохновляющих перспектив будущего. У истоков статистики как науки, а не только практической деятельности стояли две школы: английская научная школа политических арифметиков и немецкая описательная школа. Английская научная школа политических арифметиков возникла в середине XVIIв. и ставила целью изучать общественные явления с помощью числовых характеристик. В центре исследования были статистические методы, теория статистики. Явления изучались не в статике, а в динамике. Предметом статистического изучения являлись не отдельные, а массовые общественные явления, поскольку закономерность может проявиться лишь при достаточно большом объёме анализируемой совокупности. Школа английских арифметиков имела два направления: демографическое, представленное Д. Граунтом и Э. Галлеем, и статистико-экономическое, разработанное В. Петти. Английские учёные впервые не описывали социально-экономические явления, а давали им числовую оценку. Конкретными цифрами они стремились охарактеризовать состояние и развитие общества, показать закономерности развития общественных явлений на основе изучения массовых данных. Идеи Д.Граунта, Э. Галлея, В. Петти имели последователей в Англии и других европейских государствах. Наибольшее развитие школа политических арифметиков получила в XVII и XVIIIвв. в Англии, Голландии, Франции. История показала, что именно эта научная школа явилась истоком современной теории статистики. Представители описательной статистики стремились систематизировать существующие способы описания государств, создать теорию плохого описания, разработать её детальную схему. Однако они вели описание только в словесной форме, без цифр, вне динамики и связи явлений, т.е. без отражения особенностей развития государства. Собирался информационный материал, который впоследствии не анализировался. Описывался последний период, предмет и методы науки не были чётко определены. В трудах немецких учёных описывались государства, их устройство, быт и нравы населения, климат, финансы, армия, религия. Основанием описательной школы был немец Г. Конрринг, который разработал систему описания государственного устройства. Дальнейшее развитие направление получило в работах Г. Ахенвалля (описание политического состояния и достопримечательностей государсв) и А. Шлицера (опроверг представление Ахенвалля и считал, что предметом статистики является все общество). Школа просуществовала более 150 лет, не меняя своих теоретических основ. Содержание, задачи, предмет изучения статистики в понимании представителей этого направления были далеки от современного взгляда на статистику как на науку. В первой половине XIXв. возникло третье направление статистической науки - статистико-математическое. Особый вклад в это направление внёс бельгийский статистик Адольф Кетле. По правилам, разработанным А. Кетле, с середины XIXв. в развитых странах проводятся регулярные переписи населения. Он стал основоположником учения о средних величинах. По инициативе учёного для координации развития статистики проводились международные статистические конгрессы, в 1885 г. основан международный статистический институт, существующий до настоящего времени. В XIX в. развитию статистической методологии способствовали также труды английских учёных Ф. Гальтона, К. Пирсона, М. Митчела, В. Госсета, внёсших значительный вклад в разработку теории корреляции, изучения взаимосвязей явлений. Ф. Гальтон применил статистические методы к проблеме наследственности. К. Пирсон разрабатывал вопросы количественной оценки связи между явлениями. М. Митчелу принадлежит идея «экономического барометра», т.е. показателя, сигнализирующего об изменении ситуации. В. Госсет, писавший под псевдонимом Стьюдент, разработал теорию малой выборки. С начала XX в. при социально-экономических исследованиях уровня жизни населения, покупательского спроса, качества продукции начали применяться методы теории вероятностей, составляющей одну из отраслей прикладной математики. Наиболее известным учёным в этой области является Р.Фишер. В России развитие математической статистики интенсивно проходило с начала XX в. Появились исследования А.В. Монтовича о кривых распределения; Е.Е. Слуцкого, А.А. Чупрова о корреляционном анализе. Продолжателем А.А. Чупрова стал Н.К. Дружинин - один из ведущих специалистов по математической статистике двадцатого столетия и истории статистической науки. В 1949 г. был издан учебник Н.К. Дружинина, в котором статистика определена как наука о количественных закономерностях массовых явлений, как учение о тех принципах, на которых основывается сбор обработки этих сведений. Н.К. Дружинин последовательно отстаивал в своих трудах мысль, что статистические методы применимы не только в общественных науках, но и науках о природе. Становление статистической науки в России не обнаруживает столь чёткого обособления школ и направлений, и тем не менее можно отметить русскую описательную школу, русскую школу политических арифметиков, статистическую мысль революционеров-демократов русской социологической школы, различные технологии в русской академической статистике. Начало государственной статистики в России можно отнести к концу XII - началу XIII в., хотя первые переписи земель и населения с постоянно усложнявшейся программой проводились еще в Киевской Руси (IX - XII вв.). Реформы Петра I (1672-1725), которыми были охвачены все основные направления общественной жизни: экономика страны, административное управление, армия, культура и быт населения, а также войны вызывали потребность в полном и точном учете материальных ресурсов и населения. В этот период высший правительственный орган - Сенат - через систему коллегий не только руководил экономикой страны, но и являлся центром по проведению важнейших статистических работ, там собирались полученные материалы обследований, отчеты подведомственных коллегиям производств и заведений, а также местной администрации. Петровская реформа налоговой системы связана с появлением новой единицы, ею стала «душа» мужского пола, что потребовало подушной переписи населения - ревизии. Первая ревизия была объявлена 26 ноября 1718 г., ревизию проводила армия. В начале XVIII в. в России зарождался и текущий учет населения. Так, в 1702 г. был издан указ о подаче в Патриарший Духовный приказ приходскими священниками недельных ведомостей о родившихся и умерших. В первой половине XVIII в. проводились уже переписи рабочих фабрик и мануфактур. Первая половина XIX в. связана с новым этапом в развитии отечественной статистики. В сентябре 1802 г. в соответствии с Высочайшим манифестом императора Александра I вводится письменная отчетность министерств. Так началось операционно-структурное оформление государственной статистики в России. Этот год принято считать годом рождения российской государственной статистики. В 1811 г. впервые был создан официальный центр правительственной статистики - Статистическое отделение при Министерстве внутренних дел; сюда поступала отчетность губерний. Первым руководителем Статистического отделения был К.Ф. Герман. Среди ярких представителей русской описательной школы статистики выделяется один из первых просветителей России В.Н.Татищев (1686-1750), который поставил вопрос о едином текущем учёте населения, указал на недостатки ревизий, разработал конкретные предложения по их проведению; рост народонаселения он рассматривал в неразрывной связи с развитием экономики и культуры России. В развитии статистики видное место принадлежит представителям отечественной науки и практики. В эпоху Петра I в работах И.К. Кирилова (1689-1737) и В.Н. Татищева (1686-1750) статистика трактовалась преимущественно как описательная наука. Но уже со второй половины XIX в. на первый план выдвигается познавательное значение статистики. К представителям описательной школы относят и учённого энциклопедических знаний - М.В.Ломоносова (1711-1765). М.В. Ломоносов усовершенствовал программу обследования Татищева, разослал её в города и уезды. Материалы о населении, о природных богатствах, финансах и экономике России в разрезе сельского хозяйства, промышленности, торговли, транспорта в течение длительного времени поступали в Российскую академию наук в виде иллюстрированных статистических данных и были обработаны уже после смерти М.В.Ломоносова. Его работы не были чисто описательными, им был присущ аналитический характер. Также яркими представителями русской описательной школы являются И.К. Кириллов (1689-1737), И.И. Голиков (1735-1801), С.Н. Плещев (1752-1802), М.И. Чулков (1740-1793) и другие. Собранные ими материалы стали источником сведений по экономической теории России с древних времён до XVIII в. Основными представителями этого направления русской статистики были Д. Бернулли (1700-1782), И.Ф. Герман (1755-1815) и другие. Уже в начале XIX в. статистика нуждалась в уточнении организационных и методологических основ, что было вызвано изменениями в системе государственного управления и распространением прогрессивно-демократических идей. В этот период выходит ряд крупных работ по теории статистики. В книги «Всеобщая теория статистики. Для обучающих сей науке» К.Ф. Герман(1767-1838) изложил основные положения, раскрывающие статистику как науку. В истории развития статистики большое значение имеют работы К.И. Арсеньева (1789-1856), в которых он утверждал, что статистика в состоянии дать адекватную характеристику жизни государства. Наиболее прогрессивные для этого времени теоретические основы статистики как самостоятельной науки были созданы Д.П. Журавским (1810-1856). Он дал системное изложение основ теоретической базы статистики как науки, определение статистической науки, уделил большое внимание вопросу достоверности данных, методу группировок, раскрыл принцип единства количественного и качественного анализа. Определив статистику как «счет по категориям», Журавский отмечал, что статистика необходима для «изучения всего, относящегося к человеку». Журавский определил важнейшие разделы социальной статистики: - статистика народонаселения - необходимость его исчисления по классам и занятиям; - изучение народного быта, жилища, питания; - статистика театров, клубов, дворянских собраний, народных увеселений; - статистика учреждений, охраняющих права собственности; - статистика нищеты, бедности, сиротства; - статистика самоубийств с указанием средств, причин, званий, возраста и прочих характеристик лиц, лишивших себя жизни. Во всех предло
|
||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 911; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.025 с.) |

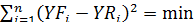 , где (1)
, где (1) (3)
(3)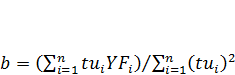 (4)
(4)


