
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. Сводка, группировка и статистические ряды распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Понятие статистической сводки как второго этапа статистического исследования. 2. Сводка в узком и широком понимании. 3. Понятие и виды статистических группировок. 4. Основные правила выбора группировочных признаков. 5. Порядок построения группировочных таблиц. 6. Понятие статистических рядов распределения и их виды. 7. Частоты вариантов статистических признаков. 8. Типологическая группировка: понятие, технология и наиболее распространенные группировочные признаки. 9. Структурная группировка: понятие, технология и наиболее распространенные группировочные признаки. 10. Назначение и особенности аналитической группировки. 11. Понятие и виды рядов динамики. 12. Основные элементы рядов динамики. 13. Моментные и интервальные, полные и неполные, изолированные и комплексные ряды динамики. Понятие статистической сводки и группировки. Виды группировок. Второй этап статистического исследования – сводка – представляет собой научную обработку первичных статистических сведений с целью выявления характерных черт изучаемой совокупности в целом и обнаружения связей между ее элементами. Статистическая группировка – это распределение единиц изучаемой совокупности на внутренне однородные группы по существенным для данного исследования признакам, которые называются группировочными. В зависимости от типа решаемой задачи и выбранного группировочного признака различают три вида статистических группировок: 1. типологическая; 2. структурная (вариационная); 3. аналитическая.
1 Типологическая группировка Типологическая группировка заключается в разделении изучаемой статистической совокупности на качественно различающиеся между собой группы. Для осуществления данной группировки обычно выбирается качественный признак или такой количественный признак, который позволяет выделить определённые устойчивые социально-экономические типы, каждый из которых соответствует одному из возможных вариантов выбранного группировочного признака. Каждому из разделов правовой статистики по отраслям права присущ свой набор наиболее распространённых группировочных признаков. Рассмотрим такой набор признаков на примере наиболее объёмного уголовно-правового раздела статистики. В частности, при статистическом изучении совершённых преступлений типологические группировки производятся по следующим основным качественным признакам: 1. форма вины (умышленные действия с прямым или косвенным умыслом, неосторожные действия); 2. категория тяжести (небольшой тяжести, средней тяжести, тяжкие, особо тяжкие); 3. мотивация (хулиганские, корыстные побуждения и т.д.); 4. характеристика личности фигурантов дела (пол, возрастная категория, занятость, семейное положение, судимость и т.д.); 5. статус фигурантов дела (подозреваемые, обвиняемые, подсудимые, осужденные, заключенные).
2 Структурная (вариационная) группировка Структурная (или вариационная) группировка заключается в разделении статистической совокупности на группы по значению количественного (варьирующего) признака и предназначена для выявления структуры и структурных сдвигов в развитии явлений и процессов. Для уменьшения количества строк и повышения наглядности группировочной таблицы всё числовое поле возможных вариантов группировочного признака разбивается на несколько интервалов. При этом границы интервалов обычно выбираются таким образом, чтобы получившиеся группы существенно различались в правовом или социально- экономическом смысле. В уголовно-правовом разделе наиболее часто применяются следующие количественные группировочные признаки: 1. возраст правонарушителей; 2. количество соучастников преступления; 3. количество потерпевших; 4. сумма ущерба; 5. сроки расследования и рассмотрения дел; 6. срок наказания; 7. число судимостей.
3 Аналитическая группировка Аналитическая группировка предназначена для изучения явлений и процессов путем выявления взаимосвязи между причинными (факторными) и результатными признаками, присущими единицам наблюдаемых статистических совокупностей. Причинными (факторными) называются признаки, под воздействием которых изменяются значения других, зависящих от них, результатных признаков. Аналитические группировки дают возможность выявить скрытые зависимости и взаимосвязи явлений в правовой сфере, что имеет важное значение для принятия практических решений и развития юридической науки.
Тема 8. Ряды динамики 1. Ряды динамики абсолютных, относительных и средних величин. 2. Аддитивная и мультипликативная модели рядов динамики. 3. Тренд, сезонный и циклический компоненты рядов динамики. 4. Понятие временного лага. 5. Сопоставимость данных в рядах динамики. 6. Смыкание рядов динамики. 7. Абсолютный прирост, темп роста, темп прироста. 8. Базисная, цепная и средняя формы показателей динамики. 9. Сглаживание рядов динамики. 10. Метод укрупнения интервалов. 11. Аналитическое сглаживание рядов динамики методом наименьших квадратов. 12. Экстраполяция динамического ряда.
Понятие, виды и назначение статистических рядов динамики Ряд динамики (или временной ряд, динамический ряд) – это расположенные в хронологическом порядке числовые значения, отражающие развитие изучаемого явления за определённый период времени. В структуру ряда динамики входят два основных элемента: 1. моменты или интервалы времени (tn); 2. уровни динамического ряда (Yn), представляющие собой числовые значения, количественно характеризующие изучаемое явление в указанные моменты (или интервалы) времени. Общее число моментов (интервалов) времени, отражённых в ряду динамики или время от первого до последнего называется длиной динамического ряда. Ряды динамики классифицируют по нескольким различным основаниям. По способу указания времени различают интервальные и моментные динамические ряды. В интервальных динамических рядах временной элемент ряда указывается в виде определённого интервала, промежутка времени, отображаемого на временной шкале в виде отрезка, имеющего чётко обозначенные границы. При этом каждый уровень такого ряда отражает общее значение изучаемого показателя за соответствующий интервал времени, получаемое путём суммирования значений этого показателя, зарегистрированных за все более мелкие отрезки времени, входящие в данный интервал. В моментных динамических рядах временной элемент ряда указывается в виде определённого момента, одной точки на шкале времени. При этом, каждый уровень такого ряда отражает значение изучаемого показателя, зафиксированное на указанный момент (дату, час и т.д.). При внешней схожести моментных и интервальных динамических рядов принципиальная разница между ними заключается в том, что в состав разных уровней одного моментного ряда могут входить одни и те же единицы изучаемой совокупности, а в интервальном ряду - не могут. Из сказанного следует, что сложение уровней допустимо только для интервальных динамических рядов, в которых эти уровни выражены в абсолютных величинах. Для всех других видов интервальных рядов и для всех моментных рядов сложение уровней одного ряда недопустимо. По расстоянию между датами или интервалам времени выделяют полные и неполные ряды. В полных интервальных рядах динамики все интервалы равны друг другу по продолжительности, а в полных моментных рядах даты (моменты) регистрации также отстоят друг от друга на равные промежутки времени. В неполных рядах динамики принцип равенства интервалов не соблюдается. По количеству одновременно изучаемых показателей - выделяют изолированные и комплексные (многомерные) ряды. При этом в изолированном ряду динамики всегда представлено развитие во времени одного показателя, а в комплексном ряду в хронологической последовательности рассматривается система из двух и более связанных между собой показателей. Компоненты уровней и назначение рядов динамики. Наблюдаемая изменчивость уровней рядов динамики объясняется одновременным действием двух составляющих: детерминированной (закономерной) и случайной. Детерминированная (закономерная) составляющая, в свою очередь, состоит из следующих компонентов: тренд (TRi), сезонный компонент (Si) и циклический компонент (Ci). Di = TRi + Si + Ci Тренд – это не циклический, плавно изменяющийся компонент уровней ряда динамики, показывающий основную тенденцию развития изучаемого явления под воздействием существенных устойчивых факторов в течение длительного времени. Структура рядов динамики тесно связана с их назначением. Ряды динамики используются для анализа закономерностей в изучаемых явлениях по следующим основным направлениям: 1. характеристика уровней развития явления во времени; 2. измерение динамики явления посредством системы специальных статистических показателей (абсолютный прирост, темп роста, темп прироста); 3. выявление и количественная оценка основной тенденции развития явления (тренда); 4. изучение сезонных и циклических колебаний регистрируемых показателей; 5. прогнозирование развития изучаемого явления.
Анализ скорости (интенсивности) динамики изучаемых показателей Визуальное восприятие динамического ряда позволяет количественно оценить уровни изучаемого явления в определённые интервалы (моменты) времени, констатировать наличие изменчивости этих уровней, и, в некоторых случаях, выявить общее направление динамики (рост или снижение значений показателя), однако, определить скорость (интенсивность) происходивших изменений можно лишь рассчитав специальные показатели динамики. Наиболее распространёнными показателями динамики являются: абсолютный прирост, темп роста, темп прироста, каждый из которых имеет три формы - базисную, цепную и среднюю.
Базисный абсолютный прирострассчитывается по формуле: ΔБi = Yi – Y1, где i - текущий номер уровня в ряду, начиная со второго; Yi – текущий уровень ряда; Y1 – начальный уровень ряда;
Цепной абсолютный прирост рассчитывается по формуле: ΔЦ i = Yi – Yi-1, где i – текущий номер уровня в ряду; Yi – текущий уровень ряда; Yi-1 – уровень ряда, предшествующий текущему;
Средний абсолютный прирост рассчитывается по формуле: ΔСР = ΣΔЦi / (n – 1), где i – текущий номер уровня в ряду, начиная со второго; ΔЦi – цепной абсолютный прирост для текущего уровня ряда; n – количество уровней в ряду (длина ряда).
Данный показатель можно рассчитать и по более простой формуле: ΔСР = (Yn – Y1)/ (n – 1), где Yn – последний (конечный) уровень ряда; Y1 – первый (начальный) уровень ряда, n – количество уровней в ряду (длина ряда);
Сглаживание рядов динамики Как уже отмечалось, среди задач, решаемых с использованием рядов динамики, одной из важнейших является задача выявления тренда. Процесс нивелирования слишком сильных колебаний уровней ряда с целью выявления тренда называется сглаживанием динамического ряда. Различают два вида сглаживания: эмпирическое (механическое) и аналитическое, которые, в свою очередь, могут реализовываться различными методами. Наиболее распространённым методом эмпирического сглаживания является метод скользящей средней, который заключается в замене уровней сглаживаемого ряда на средние значения уровней за несколько смежных интервалов. Построение сглаженного ряда осуществляется следующим образом. Определённое количество интервалов (в случае интервального ряда) или периодов времени между фиксированными моментами (в случае моментного ряда), начиная с первого, объединяются в укрупнённый интервал сглаживания. Количество уровней, входящих в интервал сглаживания, называется порядком скользящей средней (К). Вычисляется средняя арифметическая уровней, входящих в интервал сглаживания (сумма всех уровней, вошедших в этот интервал, делённая на К) и полученное значение заносится в создаваемый сглаженный ряд качестве первого уровня. Затем интервал сглаживания сдвигается и в качестве его начального уровня выбирается второй уровень исходного ряда при неизменном значении К (т.е. интервал сглаживания смещается по исходному ряду на один уровень от его начала к концу) и по новому составу интервала сглаживания вновь вычисляется средняя арифметическая входящих в него уровней, значение которой заносится в создаваемый сглаженный ряд качестве второго уровня. Таким образом, интервал сглаживания как бы скользит по исходному ряду динамики, и эта процедура повторяется до тех пор, пока не достигает конечного уровня этого исходного ряда. Чтобы увеличить степень сглаженности ряда можно увеличить величину порядка скользящей средней (К), но следует иметь в виду, что при этом уменьшится и длина ряда (на К – 1 уровней), а значит и его информативность. В отличие от эмпирического сглаживания сущность всех методов аналитического сглаживания состоит в определении параметров математической модели рассматриваемого явления (т.е. функции, описывающей изменение изучаемого показателя) и использовании этой модели для вычисления теоретических (сглаженных) уровней показателя как в пределах фактически наблюдаемого временного ряда, так и за его пределами. Конкретный метод аналитического сглаживания определяется тем, какой из следующих наиболее применимых видов функции выбран: - линейная: Yt = а + b . t; - показательная: Yt = а . bt; - параболическая: Yt = a + b . t +c . t2 Наиболее применяемым методом аналитического сглаживания является сглаживание по прямой методом наименьших квадратов, при котором для линейной функции вычисляются такие значения параметров (а и b), при которых выполняется следующее условие:
n – длина ряда (количество уровней); i – текущий номер уровня; YFi – уровни фактического (исходного) ряда; YRi – уровни расчётного (теоретического) ряда, определяемые из уравнения: YRi = а + b . ti, где (2) а – уровень ряда на момент времени t = 0; b – коэффициент расчётной скорости ряда; ti – условный номер интервала (момента) времени. Поскольку значения ti всегда известны, то для вычисления теоретических уровней остаётся определить значения параметров а и b. Для упрощения вычисления данных параметров необходимо заменить реальные номера интервалов (моментов) времени исходного ряда на условные номера таким образом, чтобы сумма этих номеров стала равной нулю. Осуществляется эта замена следующим образом: если длина исходного ряда (количество имеющихся уровней) выражается нечётным числом, то срединному уровню присваивается номер 0, предыдущий уровень получает отрицательный условный номер -1, предшествующий ему уровень – условный номер -2 и т.д. Уровни, следующие за срединным в сторону увеличения номеров, получают положительные условные номера +1, +2 и т.д. Если же длина исходного ряда – число чётное, то уровни первой половины ряда получают отрицательные нечётные условные номера (считая от последнего уровня этой половины к первому) -1, -3, -5 и т.д., а уровни второй половины ряда получают положительные нечётные условные номера (считая от первого уровня этой половины к последнему) +1, +3, +5 и т.д. После выполнения указанной замены параметры а и b уравнения (2) могут быть определены по следующим упрощённым формулам:
tui - условные номера интервалов (моментов). Таким образом, параметр а представляет собой средний уровень исходного ряда, а параметр b - коэффициент скорости динамики расчётного (теоретического) ряда. Заменив в уравнении (2) параметры а и b их вычисленными числовыми значениями, мы получим простую формулу, на основе которой для каждого условного номера интервала рассчитывается свой теоретический уровень. Последовательность этих расчётных уровней, соотнесённых с имеющимися в исходном ряду интервалами (моментам) времени и будет представлять собой аналитически сглаженный ряд динамики. Если последовательность условных номеров интервалов продолжить за временные пределы исходного ряда (в будущее), то вычисление для них по той же формуле теоретических уровней будет являться экстраполяцией исходного ряда, а сами эти уровни будут представлять собой статистический прогноз значения изучаемого показателя на предстоящие периоды.
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |

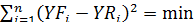 , где (1)
, где (1) (3)
(3)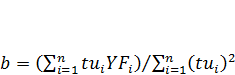 (4)
(4)


