
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Статистическая сводка и группировкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
3.1. Понятие сводки и группировки, их виды · Процесс упорядочения, систематизации и обобщения данных статистического наблюдения называется СТАТИСТИЧЕСКОЙ СВОДКОЙ. Сводка включает комплекс операций: 1) группировка единиц наблюдения; 2) разработка системы статистических показателей для характеристики групп и объекта в целом; 3) подсчёт итогов по каждой выделенной группе и по всему объекту; 4) представление результатов группировки и сводки в виде статистических таблиц. Отдельные единицы статистической совокупности объединяются в группы при помощи метода группировки. · ГРУППИРОВКОЙ называется расчленение множества единиц изучаемой совокупности на группы (подсистемы, классы, подгруппы) по определённым существенным для них признакам. · Признак, по которому производится разбивка единиц совокупности на отдельные группы, называется ГРУППИРОВОЧНЫМ ПРИЗНАКОМ (или, основанием группировки). В зависимости от целевого назначения выделяют следующие виды статистических группировок. 1. ТИПОЛОГИЧЕСКАЯ группировка служит для выделения социально-экономических типов в разнородной совокупности (группировка государств по уровню экономического развития; населения по принадлежности к общественным группам) 2. СТРУКТУРНАЯ группировка используется для разделения однородной совокупности на группы, характеризующие её структуру, по величине (значению) варьирующего признака. 3. АНАЛИТИЧЕСКАЯ группировка служит для исследования взаимосвязи между явлениями и их признаками. Взаимосвязь проявляется в том, что с возрастанием значений факторного признака систематически возрастает или убывает среднее значение результативного признака. Особенности аналитической группировки: в основу группировки положен факторный признак; каждая выделенная группа характеризуется средним значением результативного признака. В зависимости от количества группировочных признаков группировки бывают простые и сложные (комбинационные) группировки. По очерёдности обработки информации выделяют первичные и вторичные группировки. 3.2. Принципы определения числа групп (интервалов) группировки Число групп в группировке зависит от вида группировочного признака (атрибутивный или количественный), характера его вариации, а также от задач исследования.
ü Если в качестве группировочного выбран атрибутивный признак, то число групп в группировке будет таким, каково число разновидностей (видов, градаций) этого признака. В случаях, когда атрибутивный признак имеет большое число разновидностей (профессия, наименование выпускаемой продукции, наименование товара) и перечислить их все невозможно или нецелесообразно, то используют классификации. ü Если группировка проводится по количественному признаку, то число групп определяется исходя из объема совокупности (числа единиц исследуемого объекта) и степень вариации группировочного признака: а) при группировке по дискретному признаку, принимающему небольшое число значений, число групп будет равно числу этих значений (напр., разряд рабочего); б) если дискретный признак принимает много значений, и выделение такого числа групп невозможно, или группировочный признак – непрерывный, в этом случае для определения числа групп (n) можно использовать формулу Стерджесса: n = 1 + 3,322 lgN, где N - число единиц совокупности. После определения числа групп определяют интервалы группировки. · ИНТЕРВАЛ – промежуток между максимальным и минимальным значениями признака в группе. Интервалы бывают: равные и неравные (в свою очередь, могут быть произвольными, прогрессивно возрастающими или убывающими, специализированными); открытые и закрытые. Если строится группировка с равными интервалами (т.е. разность между максимальным и минимальным значением признака для каждой группы одинакова), то величина интервала (h) определяется по формуле: 3.3. Статистические ряды распределения После определения группировочного признака и границ групп строится ряд распределения (табл. 3). · ВАРИАНТА (ВАРИАНТ) – это отдельные значения признака, которые он принимает в ряду распределения. · ЧАСТОТА – число единиц совокупности, принимающих данное значение признака, численность каждой группы вариационного ряда. Сумма всех частот определяет численность всей совокупности, её объём. · Частоты, выраженные в долях единицы или в процентах к итогу, называют ЧАСТОСТЯМИ (относительными частотами).
Таблица 3 - Понятие и виды статистических рядов распределения
Для анализа рядов распределения используется их графическое изображение, позволяющее судить о форме распределения. Для изображения дискретного ряда применяется ПОЛИГОН ЧАСТОТ (ЧАСТОСТЕЙ), а интервального – ГИСТОГРАММА. 3.4. Анализ частотных распределений В вариационных рядах распределения можно заметить определённую зависимость между изменением значений варьирующего признака и частот: частоты в этих рядах с увеличением значения варьирующего признака сначала увеличиваются, а затем после достижения какой-то максимальной величины в середине ряда уменьшаются. Это свидетельствует о том, что частоты в вариационных рядах изменяются ЗАКОНОМЕРНО в связи с изменением варьирующего признака. Такие закономерности называются ЗАКОНОМЕРНОСТЯМИ РАСПРЕДЕЛЕНИЯ. Цель статистического изучения вариационных рядов - выявление закономерности распределения и оценка ее характера. Закономерности распределения наиболее отчётливо проявляются только при массовом наблюдении. Поэтому основной путь выявления таких закономерностей состоит в правильном построении вариационных рядов распределения для достаточно большой численности статистической совокупности, оптимальных числе групп и величине интервала, при которых закономерность распределения видна более отчётливо. Из математической статистики известно, что если увеличить объём совокупности и уменьшить интервал группировки, то полигон (гистограмма) распределения всё более и более будет приближаться к некоторой плавной линии - кривой распределения. КРИВАЯ РАСПРЕДЕЛЕНИЯ - графическое изображение вариационного ряда в виде непрерывной линии изменения частот, функционально связанного с изменением вариант. Получение кривой распределения на основе полигона (гистограммы) можно представить лишь для гипотетического случая (бесконечно большое число единиц совокупности и бесконечно малая ширина интервала ряда). Только при этих идеализированных условиях кривая распределения будет отражать функциональную связь между значениями признака и соответствующими им частотами и представлять так называемое теоретическое распределение.
ТЕОРЕТИЧЕСКОЙ КРИВОЙ РАСПРЕДЕЛЕНИЯ называется кривая, выражающая общую закономерность данного типа распределения в чистом виде, исключающая влияние случайных для него факторов. При проведении анализа вариационных рядов целесообразно свести эмпирическое распределение к одному из хорошо известных видов теоретического (рассматриваются математической статистикой). При этом теоретическое распределение играет роль некоторой идеализированной модели эмпирического распределения, а сам анализ вариационных рядов сводится к сопоставлению эмпирического и теоретического распределений и определению степени различия между ними. В статистической практике встречаются следующие разновидности кривых распределения: а) ОДНОВЕРШИННЫЕ КРИВЫЕ - характерны для однородных совокупностей: симметричные (в симметричных распределениях частоты любых двух вариант, равноотстоящих в обе стороны от центра распределения, равны между собой, значения средней, моды и медианы совпадают), умеренно асимметричные, крайне асимметричные; б) МНОГОВЕРШИННЫЕ КРИВЫЕ (многовершинность свидетельствует о неоднородности изучаемой совокупности; появление двух и более вершин требует перегруппировки данных с целью выделения более однородных групп). ВЫЯСНЕНИЕ ОБЩЕГО ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ предполагает: - оценку его однородности с использованием структурных средних (мода, мендиана, перцентили (квартили, децили)) и показателей вариации (см. тема 5); - вычисление показателей асимметрии и эксцесса. Наиболее распространённый способ определения показателя (коэффициента) асимметрии ( Если As = 0, то распределение считается симметричным. При As меньше нуля - левосторонняя асимметрия (правая ветвь кривой короче, мода больше медианы и больше средней). При As больше нуля - правосторонняя асимметрия (левая ветвь короче, средняя больше медианы и больше моды). As более 0,5 (независимо от знака) считается значительной; если она меньше 0,25 - незначительной. Для симметричных распределений может быть рассчитан показатель эксцесса (Ex).
Наиболее точно Ех определяется по формуле с использованием центрального момента четвёртого порядка:
Можно воспользоваться упрощенной формулой: В нормальном распределении Ex = 0, в плосковершинном распределении Ex отрицательный, и в островершинном Ех положительный. Если на практике часто встречается один и тот же тип распределения частот (например, распределение населения по уровню доходов в различных странах), его целесообразно описать с помощью математической формулы, которая может служить для сравнения и обобщения различных совокупностей аналогичных данных. В статистике широко используются следующие ВИДЫ ТЕОРЕТИЧЕСКИХ РАСПРЕДЕЛЕНИЙ: нормальное, биномиальное, распределение Пуассона и др. Каждое из теоретических распределений имеет свою специфику и область применения в различных отраслях знания. Чаще всего обращаются к НОРМАЛЬНОМУ РАСПРЕДЕЛЕНИЮ, так как оно отражает распределение частот в совокупности под действием большого числа независимых факторов и причин, из которых ни одна не является преобладающей. Такая закономерность проявляется, например, в распределении отклонений в производственном процессе при нормальном уровне организации производства и технологии; в разбросе отклонений параметров качества от среднего значения; в распределении населения определённого возраста по размерам. Нормальное распределение полностью определяется двумя параметрами (средней арифметической и СКО) и описывается формулой
Часто возникают распределения, хотя и не отвечающие строго нормальному закону (нормальному распределению), но имеющие с ним сходство. СВОЙСТВА НОРМАЛЬНОЙ КРИВОЙ РАСПРЕДЕЛЕНИЯ: 1) функция нормального распределения - ЧЁТНАЯ, т. е. f(-t) = f(+t). Следовательно, изображающая её кривая расположена симметрично относительно оси ординат, т. е. 2) функция имеет бесконечно малые значения при t = ± 3) функция имеет максимум при t = 0, т.е. кривая распределения модального значения достигает при t = 0 или при 4) при t = ± 1 функция даёт точки перегиба, следовательно, при отклонении значений признака
5) если случайная величина представляет сумму двух независимых случайных величин, следующих каждая нормальному закону, то она тоже следует нормальному закону. Объективную оценку соответствия эмпирического распределения нормальному можно получить с использованием особых статистических показателей - КРИТЕРИЕВ СОГЛАСИЯ (К.Пирсона (хи - квадрат), В.И. Романовского, А.Н. Колмогорова и Б.С. Ястремского).
3.5. Структурные характеристики вариационного ряда В качестве характеристик вариационных рядов рассчитываются так называемые структурные средние – мода и медиана. МОДА (модальное значение признака) отражает типичное, наиболее распространённое значение признака в изучаемой совокупности. МОДА (Мо) - это варианта, наиболее часто повторяющаяся в изучаемой совокупности. Пример определения моды по несгруппированным данным: рабочие бригады, состоящей из 9 человек, имеют следующие тарифные разряды: 4 3 4 5 3 3 6 2 6; в данной бригаде больше всего рабочих имеют 3-й разряд, он и будет модальным. В дискретных рядах распределения модой является варианта с наибольшей частотой. Если в ряду распределения два или несколько значений признака встречаются чаще других и одинаково часто, ряд называют мультимодальным или бимодальным. Наличие двух и более модальных значений признака говорит о неоднородности совокупности, возможно представляющей собой агрегат нескольких совокупностей с разными модами. Но всё-таки чаще встречаются ряды распределения с одной модой. В интервальном вариационном ряду при непрерывной вариации признака, каждое значение признака встречается только один раз. В этом случае модой является условное значение признака, вблизи которого ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ[2] достигает максимума. Для расчёта моды в интервальном вариационном ряду сначала определяют модальный интервал (интервал, которому соответствует наибольшая плотность распределения), а затем рассчитывают моду по формуле:
МЕДИАНОЙ (Ме) в статистике называется значение признака, расположенное в середине упорядоченного (ранжированного) ряда. Медиана выполняет функции средней величины для неоднородной (не подчиняющейся нормальному закону распределения) совокупности. Для определения медианы по несгруппированым данным необходимо сначала произвести ранжирование этих данных: ранжированный ряд разрядов рабочих бригады: 2 3 3 3 4 4 5 6 6, центральным в этом ряду является 4-й разряд, следовательно, данный разряд и будет медианным. Если ранжированный ряд имеет чётное число единиц, то медиана определяется как средняя арифметическая из двух центральных значений. В дискретном вариационном ряду медианой является не требующее расчёта значение признака в той группе, в которой накопленная частота[3] превышает половину численности совокупности. Пример: имеется распределение рабочих участка по уровню квалификации:
Тарифный разряд 2 3 4 5 6 Итого Число рабочих 1 5 8 4 2 20 Накопленная частота 1 6 14 18 20
В третьей группе рабочих с 4-м разрядом накопленная частота превышает половину численности совокупности, следовательно, Ме = 4. В интервальном вариационном ряду медиана определяется по формуле:
Медианным считается интервал, для которого накопленная частота превышает половину суммы всех частот ряда. КВАРТИЛИ, ДЕЦИЛИ, ПЕРСЕНТИЛИ (перцентили, процентили) – это значения вариант, отделяющие соответственно 1/4, 2/4, 3/4 (квартили), 1/10, 2/10, …, 9/10 (децили), 1/100, 2/100, …, 99/100 (персентили) упорядоченной совокупности. Порядок расчета этих характеристик аналогичен расчету медианы.
УПРАЖНЕНИЯ Задача 3.1. Имеются данные о расходах, связанных с подготовительными работами при разведочном бурении нефтяных скважин в различных нефтеносных районах страны (в тыс. руб. на 1 м проходки). Произведите разведочный анализ выборки: 1) постройте статистический ряд распределения; 2) изобразите результаты группировки в таблице, изобразите ряд распределения с помощью гистограммы, полигона и кумуляты, оцените характер распределения; 3) вычислите характеристики вариационного ряда (размах, среднее значение, моду, медиану, дисперсию, среднее квадратическое отклонение (СКО), коэффициент, вариации, структурные характеристики вариационного ряда (децили и квартили), асимметрию (скос), эксцесс). Сформулируйте выводы.
Результаты построения статистического ряда распределения
Результаты расчета описательных статистик распределения
Задача 3.1. По данным об обводненности нефти по фонду насосных скважин (%):
Произведите разведочный анализ выборки: 1) постройте статистический ряд распределения; 2) изобразите результаты группировки в таблице, изобразите ряд распределения с помощью гистограммы, полигона и кумуляты, оцените характер распределения; 3) вычислите характеристики вариационного ряда (размах, среднее значение, моду, медиану, дисперсию, среднее квадратическое отклонение (СКО), коэффициент, вариации, структурные характеристики вариационного ряда (децили и квартили), асимметрию (скос), эксцесс). Сформулируйте выводы. Результаты построения статистического ряда распределения
Результаты расчета описательных статистик распределения
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 996; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.112.2 (0.011 с.) |

 , где xmax и xmin – соответственно, максимальное и минимальное значение группировочного признака в совокупности.
, где xmax и xmin – соответственно, максимальное и минимальное значение группировочного признака в совокупности. ):
):  или
или  , где
, где 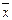 - среднее значение признака;
- среднее значение признака;  - мода, модальное значение признака (варианта, расположенная в центре упорядоченного ряда);
- мода, модальное значение признака (варианта, расположенная в центре упорядоченного ряда);  - среднее квадартическое отклонение; Р – удельный вес (в %) количества тех вариант, которые превосходят среднюю арифметическую в общем количестве вариант данного ряда; 50 – удельный вес (в %) вариант, превосходящих среднюю арифметическую ряда нормального распределения.
- среднее квадартическое отклонение; Р – удельный вес (в %) количества тех вариант, которые превосходят среднюю арифметическую в общем количестве вариант данного ряда; 50 – удельный вес (в %) вариант, превосходящих среднюю арифметическую ряда нормального распределения. , где -
, где - 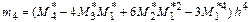 - условный центральный момент четвертого порядка.
- условный центральный момент четвертого порядка.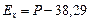 , где Р – удельный вес (в %) количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения (в ту или другую сторону от величины средней в общем количестве вариант данного ряда); 38,29 – удельный вес (в %) количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения (в ту или другую сторону от величины средней в общем количестве вариант ряда нормального распределения).
, где Р – удельный вес (в %) количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения (в ту или другую сторону от величины средней в общем количестве вариант данного ряда); 38,29 – удельный вес (в %) количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения (в ту или другую сторону от величины средней в общем количестве вариант ряда нормального распределения). , где
, где  - ордината кривой нормального распределения;
- ордината кривой нормального распределения;  - стандартизованная (нормированная) величина;
- стандартизованная (нормированная) величина;  - математические постоянные;
- математические постоянные;  - варианты вариационного ряда и их средняя величина;
- варианты вариационного ряда и их средняя величина;  - среднее квадратическое отклонение.
- среднее квадратическое отклонение.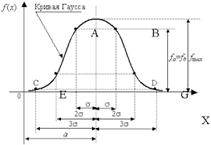

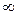 , т.е. ветви кривой удалены в бесконечность и асимптотически приближаются к оси абсцисс; чем больше значения признака отклоняются от средней, тем реже встречаются;
, т.е. ветви кривой удалены в бесконечность и асимптотически приближаются к оси абсцисс; чем больше значения признака отклоняются от средней, тем реже встречаются; ; величина максимума составляет
; величина максимума составляет 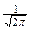 .
. от средней
от средней 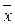 в положительном и отрицательном направлениях на одно стандартное (нормированное) отклонение (±
в положительном и отрицательном направлениях на одно стандартное (нормированное) отклонение (±  от х) кривая даёт переход от выпуклости к вогнутости;
от х) кривая даёт переход от выпуклости к вогнутости; , где
, где 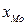 - нижняя граница модального интервала;
- нижняя граница модального интервала;  - величина модального интервала;
- величина модального интервала;  - частота модального интервала;
- частота модального интервала;  - частота предмодального и постмодального интервала.
- частота предмодального и постмодального интервала. , где
, где  - нижняя граница интервала, содержащего медиану;
- нижняя граница интервала, содержащего медиану;  - сумма частот, численность совокупности;
- сумма частот, численность совокупности;  - сумма накопленных частот, предшествующих медианному интервалу;
- сумма накопленных частот, предшествующих медианному интервалу;  - частота медианного интервала.
- частота медианного интервала.


