
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Теоретические основы и методологияСодержание книги
Поиск на нашем сайте КОНСПЕКТ ЛЕКЦИЙ И ЗАДАНИЯ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ Для обучающихся по направлению подготовки магистров Нефтегазовое дело»
Составитель: к. с. н., доцент Дружинина И.В.
Ó Федеральное государственное бюджетное образовательное Учреждение высшего образования «Тюменский государственный нефтегазовый университет», 2015 г. ТЕМА 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И МЕТОДОЛОГИЯ СТАТИСТИКИ
Термин «статистика» (от латинского слова «status» – состояние, определенное положение вещей) в настоящее время употребляется в основном в трех значениях: 1) ОТРАСЛЬ ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ, направленная на сбор, обработку и анализ данных, характеризующих социально-экономическое развитие страны, ее регионов, отраслей экономики, отдельных предприятий; 2) ОТРАСЛЬ ОБЩЕСТВЕННЫХ НАУК, занимающаяся разработкой теоретических положений и методов, которые используются статистической практикой; как наука, статистика – это еще и УЧЕНИЕ О СИСТЕМЕ ПОКАЗАТЕЛЕЙ, дающих всестороннее представление об общественных явлениях, о народном хозяйстве в целом и отдельных его отраслях; - это ИНСТРУМЕНТ ПОЗНАНИЯ, используемый в различных науках для установления специфических закономерностей, которые действуют в конкретных массовых явлениях, изучаемых данной наукой; 3) СИНОНИМ СЛОВА "ДАННЫЕ", т.е. числовые (или цифровые) данные, характеризующие различные стороны жизни государства: политические отношения, культуру, население, производство, торговлю и т.д. Как наука статистика имеет свой предмет и специфические методы исследования. · ПРЕДМЕТ СТАТИСТИКИ - количественная сторона качественно определённых массовых социально-экономических явлений и процессов, их структура и распределение, размещение в пространстве, движение во времени. Статистика также выявляет действующие количественные зависимости, тенденции и закономерности развития явлений, причём в конкретных условиях места и времени. Теоретическую основу статистикисоставляют следующие важнейшие категории: совокупность; вариация; признак; закономерность. · СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ - объект статистического исследования (в каждом конкретном случае), т.е. множество единиц, обладающих массовостью, качественной однородностью и наличием вариации. Например, множества промышленных предприятий, семей, студентов, граждан какой-либо страны. · Каждый отдельно взятый элемент данного множества называется ЕДИНИЦЕЙ СОВОКУПНОСТИ. Единицы совокупности обладают определёнными свойствами, качествами. · Свойство, качество единицы совокупности, отличающее её от других единиц, называется ПРИЗНАКОМ. Признаки различаются способами их измерения, характером выражения, вариации и другими особенностями, влияющими на приёмы статистического изучения (табл. 1). · Под КАЧЕСТВЕННОЙ ОДНОРОДНОСТЬЮ СТАТИСТИЧЕСКОЙ СОВОКУПНОСТИ понимается сходство единиц по каким-либо существенным признакам (т.е. определяющим главное содержание изучаемого явления), но различие по каким-либо другим. Например, качественная однородность множества студентов заключается в принадлежности этих лиц к определённой социальной группе.
Таблица 1 - КЛАССИФИКАЦИЯ ПРИЗНАКОВ В СТАТИСТИКЕ
· ВАРИАЦИЯ ПРИЗНАКОВ - различие величины того или иного признака у разных единиц совокупности - обусловлена различным сочетанием условий, в которых развиваются или существуют единицы совокупности. Именно наличие вариации предопределяет необходимость статистики. Вариация признаков отражается статистическим распределением, которое имеет большое практическое и научное значение. Важнейшей категорией статистики является статистическая закономерность. · СТАТИСТИЧЕСКАЯ ЗАКОНОМЕРНОСТЬ – это количественная закономерность изменения в пространстве и во времени массовых явлений и процессов общественной жизни, состоящих из множества элементов (единиц совокупности). Важнейшая особенность статистической закономерности (главное ее отличие от других видов закономерностей) заключается в том, что она свойственна не отдельным единицам совокупности, а всей их массе (совокупности в целом) и проявляется только при достаточно большом числе наблюдений и только в среднем. Это обусловливает её взаимосвязь с ЗАКОНОМ БОЛЬШИХ ЧИСЕЛ, основное содержание которого заключается в том, что в сводных статистических характеристиках действия элементов случайности взаимопогашаются, хотя они и могут проявляться в индивидуальных признаках единиц статистической совокупности. Предмет статистики имеет ряд особенностей: 1) исследуются не отдельные факты, а массовые социально-экономические явления и процессы (т.е. множества отдельных фактов, обладающих как индивидуальными, так и общими признаками); 2) статистика изучает, прежде всего, количественную сторону общественных явлений и процессов в конкретных условиях места и времени; количественную характеристику статистика выражает через определённого рода числа - СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ[1]; 3) статистика характеризует структуру общественных явлений, т.е. их внутреннее строение, при этом выявляются составные части социально-экономических явлений, эти составные части сопоставляются с явлением в целом и между собой, данная структура сравнивается с другими однотипными структурами, а также с заданной (нормативной или плановой) и выявляются причины отклонений; 4) изменения уровня явления и его структуры исследуются во времени, при этом анализ динамики включает: установление уровня явления на определённые моменты или промежутки времени и среднего уровня, выявление характера изменений за каждый промежуток времени и в целом, определение величины и темпов изменения, установление основной тенденции изменений, их закономерности и составление статистического прогноза. 5) выявление связей; явления общественной жизни взаимосвязаны и взаимообусловлены: изменение одних явлений предопределяет другие; наибольшее значение имеет выявление причинно-следственных связей для того, чтобы воздействовать на общественные явления с целью их изменения в интересах общества; с помощью специальной методологии статистика определяет количественные связи между общественными явлениями. Для изучения своего предмета статистика разрабатывает и применяет разнообразные МЕТОДЫ, совокупность которых образует СТАТИСТИЧЕСКУЮ МЕТОДОЛОГИЮ. Применение в статистическом исследовании конкретных методов обусловлено поставленными при этом задачами и зависит от характера исходной информации. Всё многообразие статистических методов систематизируется по их целевому применению в трёх стадиях экономико-статистического исследования, выполняемых последовательно: 1) сбор первичной информации; 2) статистическая сводка и обработка первичной информации; 3) анализ статистической информации. На начальной стадии статистического исследования применяется МЕТОД МАССОВОГО СТАТИСТИЧЕСКОГО НАБЛЮДЕНИЯ. Важнейшим методом второй стадии является МЕТОД СТАТИСТИЧЕСКОЙ СВОДКИ И ГРУППИРОВКИ. Одним из этапов процесса группировки является построение РЯДОВ РАСПРЕДЕЛЕНИЯ, т.е. распределение единиц наблюдения по величине или значению признака. Результаты статистической сводки и группировки оформляются в виде СТАТИСТИЧЕСКИХ ТАБЛИЦ. Для третьей стадии статистического исследования характерны: - МЕТОД ОБОБЩАЮЩИХ СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ (включает применение абсолютных, относительных и средних величин); - ИНДЕКСНЫЙ МЕТОД; - ДИНАМИЧЕСКИЕ РЯДЫ; - КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ; - МЕТОДЫ МНОГОМЕРНОГО СТАТИСТИЧЕСКОГО АНАЛИЗА; - МЕТОД СТАТИСТИЧЕСКИХ ГРАФИКОВ; - БАЛАНСОВЫЙ МЕТОД. Познавательные задачи статистики, как науки: 1)изучение уровня, структуры, динамики и взаимосвязей массовых социально-экономических явлений; 2)разработка и совершенствование системы статистических показателей, приёмов и методов сбора, обработки, анализа и хранения статистической информации.
УПРАЖНЕНИЯ Задача 8.1. Для изучения использования рабочего времени рабочими цеха по ремонту промыслового оборудования было проведено 10%-е выборочное обследование 100 рабочих методом случайного бесповторного отбора. В результате обследования получены данные о распределении рабочих по времени выполнения производственной операции.
С вероятностью 0,954 определите пределы, в которых находится средняя трудоемкость выполнения операции в цехе. Коэффициент доверия t=1,99.
Задача 8.2. На машиностроительном заводе с численностью рабочих 5000 чел. было проведено 4%-ное выборочное обследование квалификации рабочих методом случайного бесповторного отбора. В результате обследования получены следующие данные:
С вероятностью 0,997 определите пределы, в которых находится средний тарифный разряд рабочих завода. Коэффициент доверия t= 2,97.
Задача 8.3. Для изучения производительности труда токарей на машиностроительном заводе проведено 10%-е выборочное обследование 100 рабочих методом случайного бесповторного отбора. В результате обследования получены данные о часовой выработке рабочих.
С вероятностью 0,954 определите пределы, в которых находится средняя выработка одного токаря завода. Коэффициент доверия t=1,99.
Задача 8.4. По действующему фонду скважин проведено 10%-ное обследование с целью измерения обводненности продукции методом случайного бесповторного отбора. В результате обследования получены следующие данные.
С вероятностью 0,990 определите пределы, в которых находится средний уровень обводненности действующего фонда скважин. Коэффициент доверия t=2,58. УПРАЖНЕНИЯ Задача 3.1. Имеются данные о расходах, связанных с подготовительными работами при разведочном бурении нефтяных скважин в различных нефтеносных районах страны (в тыс. руб. на 1 м проходки). Произведите разведочный анализ выборки: 1) постройте статистический ряд распределения; 2) изобразите результаты группировки в таблице, изобразите ряд распределения с помощью гистограммы, полигона и кумуляты, оцените характер распределения; 3) вычислите характеристики вариационного ряда (размах, среднее значение, моду, медиану, дисперсию, среднее квадратическое отклонение (СКО), коэффициент, вариации, структурные характеристики вариационного ряда (децили и квартили), асимметрию (скос), эксцесс). Сформулируйте выводы.
Результаты построения статистического ряда распределения
Результаты расчета описательных статистик распределения
Задача 3.1. По данным об обводненности нефти по фонду насосных скважин (%):
Произведите разведочный анализ выборки: 1) постройте статистический ряд распределения; 2) изобразите результаты группировки в таблице, изобразите ряд распределения с помощью гистограммы, полигона и кумуляты, оцените характер распределения; 3) вычислите характеристики вариационного ряда (размах, среднее значение, моду, медиану, дисперсию, среднее квадратическое отклонение (СКО), коэффициент, вариации, структурные характеристики вариационного ряда (децили и квартили), асимметрию (скос), эксцесс). Сформулируйте выводы. Результаты построения статистического ряда распределения
Результаты расчета описательных статистик распределения
УПРАЖНЕНИЯ Задача 4.1. Имеются следующие данные о среднедушевых денежных доходах населения Тюменской области.
Вычислите относительные показатели динамики с постоянной и переменной базой сравнения. Проверьте их взаимосвязь. В качестве постоянной базы сравнения принять уровень 1 года. При расчете показателей динамики с переменной базой сравнения каждый последующий уровень сравнивается с предыдущим смежным. Задача 4.2. По данным о себестоимости 1000 м3 газа рассчитайте относительные показатели.
Задача 4.3. По данным о составе фонда скважин определите относительные показатели структуры и координации.
Задача 4.4. По данным таблицы рассчитайте относительные показатели интенсивности (уровня развития), используя следующие данные по РФ за 2012 г.
Задача 4.5. Используя значения признаков по факультетам, определите средние показатели по вузу. Формулы запишите, используя буквенные обозначения признаков. Укажите виды использованных средних. Тема 5. ПОКАЗАТЕЛИ ВАРИАЦИИ ВАРИАЦИЯ – (в переводе с лат. – изменение, колеблемость, различие) это различие значений какого-либо признака у разных единиц совокупности в один и тот же период или момент времени. Вариация порождается комплексом условий, действующих на совокупность и её единицы, и присуща всем без исключения явлениям природы и общества (за исключением законодательно закреплённых нормативных значений отдельных социальных признаков). Измерение вариации даёт возможность оценить степень влияния на изучаемый признак других варьирующих признаков. Например, установить, какие факторы и в какой степени влияют на смертность населения, финансовое положение предприятий, урожайность пшеницы и т. п. Для измерения вариации признака применяются различные обобщающие показатели. 1. Размах колебаний (вариации) (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности: 2. Формулы для расчёта среднего линейного отклонения, дисперсии, среднего квадратического отклонения зависят от того, в каком виде представлены данные (сгруппированы они или нет) (таблица 6).
Таблица 6 – Показатели вариации
Качественные (альтернативные) признаки, так же как и количественные варьируют (изменяются). Вариация альтернативного признака оценивается с помощью показателя дисперсии, определяемого по формуле: При сравнении колеблемости различных признаков в одной и той же совокупности или при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной средней арифметической используются относительные показатели рассеивания (вариации). К относительным показателям вариации относятся: 1) коэффициент осцилляции 2) относительное линейное отклонение 3) коэффициент вариации Для оценки влияния различных факторов, определяющих колеблемость индивидуальных значений признака, используется разложение общей дисперсии на составляющие: межгрупповую дисперсию и среднюю дисперсию из внутригрупповых. Общая дисперсия рассчитывается по всей совокупности и характеризует вариацию признака, обусловленную влиянием всех факторов, действующих в совокупности:
Межгрупповая дисперсия (является мерой колеблемости частных или групповых средних вокруг общей средней) характеризует вариацию признака, обусловленную влиянием фактора, положенного в основу группировки: Вариацию признака под влиянием прочих факторов (помимо признака-фактора, положенного в основу группировки), действующих в совокупности, характеризует средняя дисперсия из внутригрупповых (частных) дисперсий: Внутригрупповая (частная) дисперсия:
Между названными видами дисперсий существует определённое соотношение, которое называют ЗАКОНОМ (правилом) сложения дисперсий:
Отношение межгрупповой дисперсии к общей даст коэффициент детерминации Показатель, полученный как корень квадратный из коэффициента детерминации, называется эмпирическим корреляционным отношением: Эмпирическое корреляционное соотношение характеризует тесноту связи между результативным и факторным признаками. Чем ближе эмпирическое корреляционное отношение к 1, тем теснее связь между признаками.
УПРАЖНЕНИЯ Задача 5.1 По данным 10 газовых промыслов вычислите показатели вариации пластового давления и среднесуточного дебита: размах, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Сформулируйте выводы о характере вариации показателей работы промыслов.
МЕЖДУ ЯВЛЕНИЯМИ 6.1. Причинность, регрессия, корреляция В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие основное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения – это связь явлений и процессов, когда изменение одного из них – причины, ведет к изменению другого – следствия. Признаки по их значению для изучения взаимосвязи делятся на два вида: факторные и результативные. Социально-экономические явления представляют собой результат одновременного воздействия большого числа причин. Следовательно, при изучении этих явлений необходимо выявлять главные, основные причины, абстрагируясь от второстепенных. В основе первого этапа статистического изучения связи лежит качественный анализ изучаемого явления, т.е. исследование его природы методами экономической теории, социологии, конкретной экономики. Второй этап – построение модели связи. Третий, последний этап – интерпретация результатов, вновь связан с качественными особенностями изучаемого явления. В статистике различают функциональную связь и стохастическую. Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Такая связь проявляется во всех случаях наблюдения и для каждой конкретной единицы исследуемой совокупности. Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков. Связи между признаками и явлениями ввиду их большого разнообразия классифицируются по ряду оснований: по степени тесноты связи, направлению и аналитическому выражению. Степень тесноты корреляционной связи количественно может быть оценена с помощью коэффициента корреляции, величина которого определяет характер связи (табл.). Количественные критерии тесноты связи
По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. В случае обратной связи с увеличением значений факторного признака значения результативного убывают, и наоборот. По аналитическому выражению выделяют связи: прямолинейные (или просто линейные) и нелинейные. Если статистическая связь между явлениями может быть приближенно выражена уравнением прямой линии, то ее называют линейной; если же она выражается уравнением какой-либо кривой линии (параболы, гиперболы, показательной, экспоненциальной и т.п.), то такую связь называют нелинейной или криволинейной. Для выявления наличия связи, ее характера и направления в статистике используются методы: приведения параллельных данных; аналитических группировок; статистических графиков; корреляции. Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получит представление о ее характере. Например, изменение двух величин представлено следующими данными.
Как видно, с увеличением величины Х величина У также возрастает. Поэтому связь между ними прямая, и описать ее можно уравнением прямой, либо уравнением параболы второго порядка.
Графически взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат – результативного. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи (рис.).
При отсутствии тесных связей имеет место беспорядочное расположение точек на графике. Для социально-экономических явлений характерно, что наряду с существенными факторами, формирующими уровень результативного признака, на него оказывают влияние многие другие неучтенные и случайные факторы. Это свидетельствует о том, что взаимосвязи явлений, которые изучает статистика, носят корреляционный характер. Корреляция – это статистическая взаимосвязь между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания (средней величины) другой. В статистике принято различать следующие виды зависимостей. 1. Парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными). 2. Частная корреляция – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков. 3. Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование. Задачей корреляционного анализа является количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Теснота связи количественно выражается величиной коэффициентов корреляции, которые дают возможность определить «полезность» факторных признаков при построении уравнений множественной регрессии. Кроме того, величина коэффициента корреляции служит оценкой соответствия уравнения регрессии выявленным причинно-следственным связям. 6.2. Оценка тесноты связи Теснота корреляционной связи между факторным и результативным признаками может исчисляться с помощью таких коэффициентов: эмпирический коэффициент корреляционной связи (коэффициент Фехнера); коэффициент ассоциации; коэффициент взаимной сопряженности Пирсона и Чупрова;
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.012 с.) |

 .
.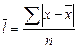





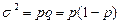 , где p – доля единиц, обладающих данным признаком; q – доля единиц, не обладающих данным признаком.
, где p – доля единиц, обладающих данным признаком; q – доля единиц, не обладающих данным признаком. ;
; ;
;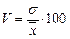 , используется для оценки типичности средней величины признака. Совокупность считается однородной, а средняя типичной для данной совокупности, если коэффициент вариации не больше 33 %.
, используется для оценки типичности средней величины признака. Совокупность считается однородной, а средняя типичной для данной совокупности, если коэффициент вариации не больше 33 %. - простая дисперсия;
- простая дисперсия;
 - взвешенная дисперсия
- взвешенная дисперсия
 .
. .
. , отражает вариацию признака только за счёт условий и причин, действующих внутри группы.
, отражает вариацию признака только за счёт условий и причин, действующих внутри группы. .
. , который характеризует долю вариации результативного признака, обусловленную признаком-фактором, положенным в основу группировки, в общей вариации признака.
, который характеризует долю вариации результативного признака, обусловленную признаком-фактором, положенным в основу группировки, в общей вариации признака. .
.



