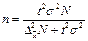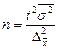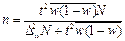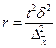Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Статистическое наблюдениеСодержание книги
Поиск на нашем сайте 2.1. Понятие и план подготовки статистического наблюдения · СТАТИСТИЧЕСКОЕ НАБЛЮДЕНИЕ - массовое, планомерное научно организованное наблюдение за явлениями социальной и экономической жизни, которое заключается в регистрации отобранных признаков у каждой единицы совокупности. Может проводиться органами государственной статистики, научно-исследовательскими институтами, экономическими и социальными службами фирм, банков, бирж. Статистическое наблюдение должно удовлетворять ряду требований: 1) наблюдаемые явления должны иметь научную (практическую) ценность; 2) непосредственный сбор массовых данных должен обеспечить полноту фактов, относящихся к рассматриваемому явлению; 3) результаты статистического наблюдения должны быть достоверны и сопоставимы. Процесс подготовки статистического наблюдения включает решение программно-методологических и организационных вопросов (таблица 2).
Таблица 2 - Содержание подготовки статистического наблюдения
Таблица 3 - Формы, виды и способы статистического наблюдения
2.2. Ошибки статистического наблюдения Как показывает практика, даже при чётко организованном и спланированном статистическом наблюдении встречаются погрешности и ошибки, требующие исправления. · Расхождение между расчетным и действительным значением изучаемых величин называется ОШИБКОЙ НАБЛЮДЕНИЯ. В зависимости от причин возникновения различают: 1) ошибки регистрации (случайные и систематические); 2) ОШИБКИ РЕПРЕЗЕНТАТИВНОСТИ ( случайные и систематические) ПРИСУЩИ ТОЛЬКО НЕСПЛОШНОМУ НАБЛЮДЕНИЮ. После получения статистических формуляров, прежде всего, проводится проверка полноты собранных в процессе статистического наблюдения данных, а затем осуществляется их логический и арифметический контроль. 2.3. Понятие выборочного метода. Ошибка выборки Статистическое исследование может осуществляться по данным несплошного наблюдения. Основная цель несплошного наблюдения – получение характеристик изучаемой совокупности по обследованной её части. Один из наиболее распространённых в статистике методов, применяющий несплошное наблюдение – выборочный метод. · Под ВЫБОРОЧНЫМ понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой её части (обычно 5 – 10 %, реже 15 – 25 % изучаемой совокупности)на основе случайного отбора. · Подлежащая изучению статистическая совокупность, из которой часть единиц отбирается для обследования, называется ГЕНЕРАЛЬНОЙ СОВОКУПНОСТЬЮ. · Некоторая часть единиц, отобранная из генеральной совокупности и подвергающаяся обследованию, называется ВЫБОРОЧНОЙ СОВОКУПНОСТЬЮ (ВЫБОРКОЙ). Значение выборочного метода состоит в следующем: 1) при минимальной численности обследуемых единиц исследование проводится в более короткие сроки и с минимальными затратами труда и денежных средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации; 2) при проведении ряда исследований выборочный метод является единственно возможным; 3) применяется для проверки данных сплошного учёта. Выборочный метод имеет важную особенность по сравнению с другими методами несплошного наблюдения: в основу отбора единиц для обследования положен принцип равных возможностей попадания в выборку каждой единицы генеральной совокупности. В результате соблюдения этого принципа исключается возможность образования выборки только за счёт лучших или худших образцов. Это предупреждает возникновение систематических ошибок. · Поскольку любая статистическая совокупность состоит из единиц с варьирующими признаками, то состав выборочной совокупности может в той или иной мере отличаться от состава генеральной совокупности. Это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности составляет ОШИБКУ ВЫБОРКИ. Величина ошибки выборки зависит от ряда факторов: 1) степени вариации изучаемого признака; 2) численности выборки; 3) методов отбора единиц в выборочную совокупность; 4) принятого уровня достоверности результата исследования. ОБЩАЯ ВЕЛИЧИНА ВОЗМОЖНОЙ ОШИБКИ ВЫБОРКИ слагается из ошибок двух видов: ошибки регистрации и ошибки репрезентативности. Первый вид ошибок при выборочном наблюдении практически исключён. Второй вид ошибок присущ только несплошному наблюдению. Ошибки репрезентативности бывают систематические и случайные. · СИСТЕМАТИЧЕСКИЕ ОШИБКИ могут возникать в связи с особенностями принятой системы отбора и обработки данных наблюдения, или в связи с нарушениями установленных правил отбора единиц для обследования. · Возникновение СЛУЧАЙНЫХ ОШИБОК РЕПРЕЗЕНТАТИВНОСТИ объясняется неравномерным распределением единиц в генеральной совокупности. Поэтому распределение отобранной для обследования совокупности единиц (выборки) не вполне точно воспроизводит распределение единиц генеральной совокупности. Величина ошибки выборки характеризует степень надёжности результатов обследования выборочной совокупности и необходима для оценки параметров генеральной совокупности. Для каждого конкретного выборочного наблюдения величина ошибки выборки может быть определена по соответствующим формулам. 2.4. Основные способы формирования выборочной совокупности Способ отбора определяет конкретный механизм или процедуру выборки единиц из генеральной совокупности и зависит от степени вариации изучаемого признака в исследуемой совокупности. В практике выборочных обследований наибольшее распространение получили следующие СПОСОБЫ ФОРМИРОВАНИЯ ВЫБОРКИ. · СОБСТВЕННО-СЛУЧАЙНАЯ ВЫБОРКА заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности. Применяется в случае незначительной вариации изучаемого признака в пределах исследуемой совокупности. При проведении отбора этим способом следует принять во внимание, что все единицы генеральной совокупности имеют равные шансы попадания в выборку. Следует также установить чёткие границы генеральной совокупности таким образом, чтобы включение или невключение в неё отдельных единиц не вызывало сомнений. Например, при обследовании студентов, необходимо чётко определиться, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов и т. п. Технически собственно-случайный отбор проводится путём жеребьёвки или с помощью таблиц случайных чисел. Собственно-случайный отбор может быть как повторным, так и бесповторным (выпавшие жребии обратно в исходную совокупность не возвращаются и в дальнейшем отборе не участвуют). МЕХАНИЧЕСКАЯ ВЫБОРКА применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определённая последовательность в расположении единиц (например, телефонные номера респондентов, списки избирателей, номера домов, квартир). Для проведения механической выборки устанавливается пропорция отбора, которая устанавливается соотнесением объёмов выборочной и генеральной совокупности. Например, при пропорции 1:50 (2%-ная выборка) отбирается каждая 50-я единица; при пропорции 1:20 (5%-ная выборка) – каждая 20 единица и т.д. ТИПИЧЕСКИЙ ОТБОР предполагает выборку из единиц из каждой типической группы собственно-случайным или механическим способом; используется в тех случаях, когда все единицы генеральной совокупности можно разбить на типические группы; вариация исследуемого признака от группы к группе – значительная. При обследованиях населения такими группами могу быть, например, районы, социальные, возрастные или образовательные группы; при обследовании предприятий – вид экономической деятельности, форма собственности и т.д. Отбор единиц в типическую выборку может быть организован либо пропорционально объёму типических групп, либо пропорционально внутригрупповой дифференциации признака. При выборке, пропорциональной объёму типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом: ni = n · Ni/N, где ni – объём выборки из i-й группы; Ni – объём i-й группы, n – численность выборочной совокупности. Отбор, пропорциональный внутригрупповой дифференциации признака, осуществляется на основе использования внутригрупповых дисперсий по каждой типической группе. СЕРИЙНЫЙ ОТБОР заключается в собственно-случайном, либо механическом отборе серий, внутри которых производится сплошное обследование единиц; удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии (упаковки с определённым количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения). КОМБИНИРОВАННЫЙ ОТБОР предполагает применение различных способов формирования выборки в комбинации. Возможно комбинировать: - типическую выборку и серийную (серии отбираются в установленном порядке из нескольких типических групп); - серийный и собственно-случайный отбор (отдельные единицы отбираются внутри серии в собственно-случайном порядке).
2.5. Средняя и предельная ошибки выборки После проведения отбора для определения возможных границ генеральных характеристик рассчитываются средняя и предельная ошибки выборки. СРЕДНЯЯ ОШИБКА ВЫБОРКИ показывает величину возможных отклонений характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности. Ошибки выборки могут быть рассчитаны для среднего значения признака и для доли альтернативного признака (табл.). В математической статистике доказывается, что генеральная средняя будет отличаться от выборочной средней на величину средней ошибки выборки (±m) только в 68,3% случаев. В 95% случаев ошибка выборки не выйдет за пределы ±2m. В 99,7% случаев разность между генеральной и выборочной средней на превзойдёт трёхкратной средней ошибки выборки (±3m) и т.д.
Таким образом, о величине ошибки выборки можно судить с определённой вероятностью, от которой зависит множитель t, называемый коэффициентом доверия. Логически связь выглядит так: чем больше пределы, в которых допускается возможная ошибка, тем с большей вероятностью судят о её величине. При заданной вероятности коэффициент доверия t определяют по таблице значений интегральной функции Лапласа j (t). Величина D = ± tm называется предельной ошибкой выборки. Зная выборочную среднюю величину признака (долю альтернативного признака в выборочной совокупности) и предельную ошибку выборки (для средней или для доли), можно определить ГРАНИЦЫ, В КОТОРЫХ ЗАКЛЮЧЕНА ГЕНЕРАЛЬНАЯ СРЕДНЯЯ (ГЕНЕРАЛЬНАЯ ДОЛЯ): для средней для доли 2.6. Определение необходимого объёма выборки При проектировании выборочного наблюдения возникает вопрос о необходимой численности выборки. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении исходя из вероятности, с которой гарантируется величина устанавливаемой ошибки, и наконец, на базе способа отбора. Для определения необходимой численности выборки исследователь должен задать уровень точности характеристики выборочной совокупности с определённой вероятностью. Необходимый объём выборки для различных способов формирования выборочной совокупности определяется исходя из формул для расчёта предельной ошибки выборки (табл.).
УПРАЖНЕНИЯ Задача 8.1. Для изучения использования рабочего времени рабочими цеха по ремонту промыслового оборудования было проведено 10%-е выборочное обследование 100 рабочих методом случайного бесповторного отбора. В результате обследования получены данные о распределении рабочих по времени выполнения производственной операции.
С вероятностью 0,954 определите пределы, в которых находится средняя трудоемкость выполнения операции в цехе. Коэффициент доверия t=1,99.
Задача 8.2. На машиностроительном заводе с численностью рабочих 5000 чел. было проведено 4%-ное выборочное обследование квалификации рабочих методом случайного бесповторного отбора. В результате обследования получены следующие данные:
С вероятностью 0,997 определите пределы, в которых находится средний тарифный разряд рабочих завода. Коэффициент доверия t= 2,97.
Задача 8.3. Для изучения производительности труда токарей на машиностроительном заводе проведено 10%-е выборочное обследование 100 рабочих методом случайного бесповторного отбора. В результате обследования получены данные о часовой выработке рабочих.
С вероятностью 0,954 определите пределы, в которых находится средняя выработка одного токаря завода. Коэффициент доверия t=1,99.
Задача 8.4. По действующему фонду скважин проведено 10%-ное обследование с целью измерения обводненности продукции методом случайного бесповторного отбора. В результате обследования получены следующие данные.
С вероятностью 0,990 определите пределы, в которых находится средний уровень обводненности действующего фонда скважин. Коэффициент доверия t=2,58.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

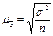




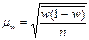


 , где r – число отобранных серий; R – число серий в генеральной совокупности;
, где r – число отобранных серий; R – число серий в генеральной совокупности;  - межсерийная дисперсия средних
- межсерийная дисперсия средних
 ,
где
,
где 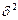 - межсерийная дисперсия доли
- межсерийная дисперсия доли

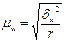
 или
или 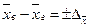 .
. или
или  .
.