
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Обобщающие статистические ПоказателиСодержание книги
Поиск на нашем сайте
Обобщающие статистические показатели получают в результате сводки и обобщения данных статистического наблюдения. Последние могут быть представлены абсолютными, относительными и средними величинами. 1. АБСОЛЮТНЫЕ СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ характеризуют абсолютные размеры изучаемых статистикой явлений и процессов в конкретных условиях места и времени: их массу, площадь, объём, протяжённость; а также могут представлять объём совокупности (т.е. число составляющих её единиц). Такие показатели всегда являются именованными числами, т.е. имеют определённую единицу измерения, они выражаются в натуральных (тонны, килограммы, мили, километры, штуки, литры и т. д.), стоимостных (рубли, доллары и др.) и трудовых единицах измерения (человеко-дни, человеко-часы, нормо-часы). 2. ОТНОСИТЕЛЬНЫЙ СТАТИСТИЧЕСКИЙ ПОКАЗАТЕЛЬ - это показатель, полученный путём сравнения статистических показателей в пространстве (между объектами), во времени (по одному и тому же объекту за разные отрезки времени) или путём сопоставления показателей разных свойств изучаемого объекта. Другими словами, - это частное от деления двух статистических показателей. Относительные показатели могут выражаться в коэффициентах, процентах, промилле, продецимилле. Относительный показатель, полученный путём сопоставления разноимённых величин, должен быть именованным. Все используемые на практике относительные статистические показатели можно подразделить на следующие виды: 1) планового задания, выполнения плана (договорных обязательств); 2) структуры; 3) динамики; 4) координации; 5) сравнения; 6) интенсивности и уровня развития и др. 1. Относительные показатели планового задания (ОППЗ) и выполнения плана (ОПВП) (договорных обязательств – ОПДО) используются для перспективного планирования деятельности предприятий и сравнения реально достигнутых результатов с намеченными ранее.
2. Относительный показатель структуры (ОПС) - соотношение структурных частей изучаемого объекта и их целого, характеризует состав совокупности: 3. Относительный показатель динамики (ОПД) - отношение уровня исследуемого процесса (явления) за данный период времени (по состоянию на данный момент времени) и уровня этого явления или процесса в прошлом:
4. Относительный показатель координации (ОПК) - соотношение двух структурных частей изучаемого объекта, также характеризует состав совокупности, но более наглядно, нежели показатели структуры:
5. Относительный показатель интенсивности (ОПИ) или уровня социально-экономического развития - соотношение разноимённых, но связанных между собой абсолютных величин, показывает насколько широко распространено изучаемое явление в той или иной среде, либо сколько единиц одной совокупности приходится на единицу другой совокупности. ОПИ – всегда величина именованная:
3. СУЩНОСТЬ И ЗНАЧЕНИЕ СРЕДНИХ ПОКАЗАТЕЛЕЙ Наиболее распространённой формой статистических показателей в статистических исследованиях является средняя величина. · СРЕДНЯЯ ВЕЛИЧИНА – это обобщённая количественная характеристика признака в статистической совокупности в конкретных условиях места и времени. Показатель в форме средней величины выражает типичные черты и даёт обобщённую характеристику однотипных явлений по одному из варьирующих признаков. Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности могут колебаться в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные. А при осреднении случайные колебания признака в силу действия закона больших чисел погашаются, уравновешиваются, и в средней величине признака белее отчётливо отражается основная линия развития, необходимость, закономерность. Главное значение средних величин состоит в их обобщающей функции, т.е. замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность. Но средняя величина только тогда будет отражать типичный уровень изучаемого признака, когда она рассчитана по качественно однородной совокупности. В таком случае метод средних должен сочетаться с методом группировок: если совокупность неоднородна – общие средние должны быть заменены или дополнены групповыми, т.е. средними величинами, рассчитанными по качественно однородным группам. Определить среднюю во многих случаях можно через ИСХОДНОЕ СООТНОШЕНИЕ СРЕДНЕЙ (ИСС) или её логическую формулу:
Для каждого показателя, используемого в социально-экономическом анализе можно составить только одно истинное исходное соотношение для расчёта средней. От того, в каком виде представлены исходные данные для расчёта средней, зависит, каким именно образом будет реализовано её исходное соотношение; для этого потребуется один из следующих видов средней величины: 1) средняя арифметическая (К = 1); 2) средняя гармоническая (К = - 1); 3) средняя геометрическая (К = 0); 4) средняя квадратическая (К = 2), кубическая (К = 3) и т.д. (табл. 4). Перечисленные средние объединяются в формуле СРЕДНЕЙ СТЕПЕННОЙ (при различной величине К): Таблица 4 - Виды средних величин
4. Средняя арифметическая и её свойства Средняя арифметическая является наиболее распространённой формой средних величин, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой и взвешенной. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ПРОСТАЯ используется в тех случаях, когда расчёт осуществляется по индивидуальным (несгруппированным) данным: СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЗВЕШЕННАЯ применяется для расчёта средней величины признака по сгруппированным данным (когда отдельные значения признака повторяются несколько раз) или по вариационным рядам распределения, которые могут быть дискретными и интервальными. Средняя арифметическая взвешенная по дискретному ряду распределения определяется по формуле: При расчёте средней по интервальному ряду (с равными интервалами) сначала вычисляют середины интервалов (переходят к дискретному ряду), а дальнейший расчёт осуществляется обычным методом определения средней арифметической взвешенной. Используя свойства средней арифметической, можно применить упрощённый способ её расчёта, называемый "способом моментов" или отсчёта от условного нуля:
УПРАЖНЕНИЯ Задача 4.1. Имеются следующие данные о среднедушевых денежных доходах населения Тюменской области.
Вычислите относительные показатели динамики с постоянной и переменной базой сравнения. Проверьте их взаимосвязь. В качестве постоянной базы сравнения принять уровень 1 года. При расчете показателей динамики с переменной базой сравнения каждый последующий уровень сравнивается с предыдущим смежным. Задача 4.2. По данным о себестоимости 1000 м3 газа рассчитайте относительные показатели.
Задача 4.3. По данным о составе фонда скважин определите относительные показатели структуры и координации.
Задача 4.4. По данным таблицы рассчитайте относительные показатели интенсивности (уровня развития), используя следующие данные по РФ за 2012 г.
Задача 4.5. Используя значения признаков по факультетам, определите средние показатели по вузу. Формулы запишите, используя буквенные обозначения признаков. Укажите виды использованных средних. Тема 5. ПОКАЗАТЕЛИ ВАРИАЦИИ ВАРИАЦИЯ – (в переводе с лат. – изменение, колеблемость, различие) это различие значений какого-либо признака у разных единиц совокупности в один и тот же период или момент времени. Вариация порождается комплексом условий, действующих на совокупность и её единицы, и присуща всем без исключения явлениям природы и общества (за исключением законодательно закреплённых нормативных значений отдельных социальных признаков). Измерение вариации даёт возможность оценить степень влияния на изучаемый признак других варьирующих признаков. Например, установить, какие факторы и в какой степени влияют на смертность населения, финансовое положение предприятий, урожайность пшеницы и т. п. Для измерения вариации признака применяются различные обобщающие показатели. 1. Размах колебаний (вариации) (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности: 2. Формулы для расчёта среднего линейного отклонения, дисперсии, среднего квадратического отклонения зависят от того, в каком виде представлены данные (сгруппированы они или нет) (таблица 6).
Таблица 6 – Показатели вариации
Качественные (альтернативные) признаки, так же как и количественные варьируют (изменяются). Вариация альтернативного признака оценивается с помощью показателя дисперсии, определяемого по формуле: При сравнении колеблемости различных признаков в одной и той же совокупности или при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной средней арифметической используются относительные показатели рассеивания (вариации). К относительным показателям вариации относятся: 1) коэффициент осцилляции 2) относительное линейное отклонение 3) коэффициент вариации Для оценки влияния различных факторов, определяющих колеблемость индивидуальных значений признака, используется разложение общей дисперсии на составляющие: межгрупповую дисперсию и среднюю дисперсию из внутригрупповых. Общая дисперсия рассчитывается по всей совокупности и характеризует вариацию признака, обусловленную влиянием всех факторов, действующих в совокупности:
Межгрупповая дисперсия (является мерой колеблемости частных или групповых средних вокруг общей средней) характеризует вариацию признака, обусловленную влиянием фактора, положенного в основу группировки: Вариацию признака под влиянием прочих факторов (помимо признака-фактора, положенного в основу группировки), действующих в совокупности, характеризует средняя дисперсия из внутригрупповых (частных) дисперсий: Внутригрупповая (частная) дисперсия:
Между названными видами дисперсий существует определённое соотношение, которое называют ЗАКОНОМ (правилом) сложения дисперсий:
Отношение межгрупповой дисперсии к общей даст коэффициент детерминации Показатель, полученный как корень квадратный из коэффициента детерминации, называется эмпирическим корреляционным отношением: Эмпирическое корреляционное соотношение характеризует тесноту связи между результативным и факторным признаками. Чем ближе эмпирическое корреляционное отношение к 1, тем теснее связь между признаками.
УПРАЖНЕНИЯ Задача 5.1 По данным 10 газовых промыслов вычислите показатели вариации пластового давления и среднесуточного дебита: размах, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Сформулируйте выводы о характере вариации показателей работы промыслов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.01 с.) |


 ,
, .
. .
. .
. .
.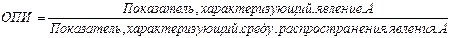

 .
.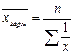
 , где W=xf
, где W=xf

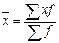




 , где А – варианта с наибольшей частотой или середина одного из центральных интервалов, имеющего как правило наибольший вес (наибольшую частоту); d – шаг или разница между любыми двумя соседними вариантами (величина интервала); m’ – момент первого порядка, т. е. средняя из значений (х – А) / d.
, где А – варианта с наибольшей частотой или середина одного из центральных интервалов, имеющего как правило наибольший вес (наибольшую частоту); d – шаг или разница между любыми двумя соседними вариантами (величина интервала); m’ – момент первого порядка, т. е. средняя из значений (х – А) / d. .
.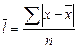





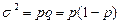 , где p – доля единиц, обладающих данным признаком; q – доля единиц, не обладающих данным признаком.
, где p – доля единиц, обладающих данным признаком; q – доля единиц, не обладающих данным признаком. ;
; ;
;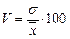 , используется для оценки типичности средней величины признака. Совокупность считается однородной, а средняя типичной для данной совокупности, если коэффициент вариации не больше 33 %.
, используется для оценки типичности средней величины признака. Совокупность считается однородной, а средняя типичной для данной совокупности, если коэффициент вариации не больше 33 %. - простая дисперсия;
- простая дисперсия;
 - взвешенная дисперсия
- взвешенная дисперсия
 .
. .
. , отражает вариацию признака только за счёт условий и причин, действующих внутри группы.
, отражает вариацию признака только за счёт условий и причин, действующих внутри группы. .
. , который характеризует долю вариации результативного признака, обусловленную признаком-фактором, положенным в основу группировки, в общей вариации признака.
, который характеризует долю вариации результативного признака, обусловленную признаком-фактором, положенным в основу группировки, в общей вариации признака. .
.


