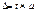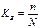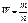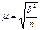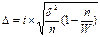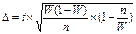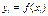Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет и задачи статистики. Закон больших чисел. Основные категории статистической методологии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Предмет и задачи статистики. Закон больших чисел. Основные категории статистической методологии. В настоящее время термин «статистика» употребляется в 3х значениях: · Под «статистикой» понимают отрасль деятельности, к-рая занимается сбором, обработкой, анализом, публикаций данных о различных явлениях общественной жизни. · Статистикой называют цифровой материал, служащий для характеристики общих явлений. · Статистикой называют отрасль знания, учебный предмет. Предметом статистики является количественная сторона массовых общих явлений в неразрывной связи с их качественной стороной. Свой предмет статистика изучает при помощи опр. категорий: · Статистическая совокупность – совокупность соц.-эк. объектов и явлений общ. Жизни, объединен. Некоторой кач. Основой н-р, совокупность пред-тий, фирм, семей. · Единица совокупности – первичный элемент статистической совокупности. · Признак – кач. Особенность единицы совокупности. · Статистический показатель – понятие отбражает количеств. харак-ки (размеры) признаков общ. явлений. · Система статистич. Показателей – совокупность статистич. показателей, отражающая взаимосвязи, к-рые существ. между явлениями. Основными задачами статистики являются: 1. всестороннее исследование глубоких преобразований эк. и соц. процессов на основе научнообоснов. системы показателей. 2. обобщение и прогнозирование тенденций развития разл. отраслей экономики в целом 3. своевременное обеспеч. надежности информации гос., хоз., эк. органов и широкой общ-сти
Особенности статистической методологии. Статистическая совокупность. Закон больших чисел. Закон больших чисел Массовый характер общественных законов и своеобразие их действий предопределяет необходимость исследования совокупных данных. Закон больших чисел порожден особыми свойствами массовых явлений. Последние в силу своей индивидуальности, с одной стороны, отличаются друг от друга, а с другой – имеют нечто общее, обусловленное их принадлежностью к определенному классу, виду. Причем единичные явления в большей степени подвержены воздействию случайных факторов, ежели их совокупность. Закон больших чисел в наиболее простой форме гласит, что количественные закономерности массовых явлений отчетливо проявляются лишь в достаточно большом их числе. Таким образом, сущность его заключается в том, что в числах, получающихся в результате массового наблюдения, выступают определенные правильности, которые не могут быть обнаружены в небольшом числе фактов. Закон больших чисел выражает диалектику случайного и необходимого. В результате взаимопогашения случайных отклонений средние величины, исчисленные для величины одного и того же вида, становятся типичными, отражающими действия постоянных и существенных фактов в данных условиях места и времени. Тенденции и закономерности, вскрытые с помощью закона больших чисел, имеют силу лишь как массовые тенденции, но не как законы для каждого отдельного случая. Свой предмет статистика изучает с помощью различных методов: · Метод массовых наблюдений · Метод статистических группировок · Метод динамических рядов · Метод индексного анализа · Метод корреляционно-регрессивного анализа связей показателей и т.д. Полит. арифметики изучали общие явления с помощью числовых характеристик. Представителями этой школы являлись Грацит – исследовал закономерности массовых явлений, Пети – создатель эк. статистики, Галей – заложил идею закона больших чисел. Статистическая совокупность - множесттво однокачественных, варьирующих явлений. Отдельные элементы,составляющие совокупности - единицы совокупности. Статист.совокупность называется однородной, если самые существенные признаки для каждой её единицы явл. в основном одинаковые и разнородные и,если объединяются разные типы явлений. Частота-повторяемость признаков в совокупности (в ряду распределения). Признак- характерная черта (свойство) или инная особенность единиц объектов явлений.Признаки делятся на:1) количественные(эти признаки выражены числами.Они играют преобладающую роль в статистике.Это признаки отдельные значения которых отличаются по величине); 2)качественные ((атрибутивные) выражаются в виде понятий, определений, выражаю-х их сущность, качественное состояние); 3) альтеранативные (качественные признаки,которые могут принимать только одно из двух противоположных значений).Признаки отдельных единиц совокупности принимают отдельные значения. Колеблиемость признаков - вариация. Единицы статистической совокупности и вариация признаков. Статистические показатели. Явления и процессы в жизни общества характеризуются статистикой с помощью статистических показателей. Статистический показаетль – это количественная оценка свойств изучаемого явления. В статистическом показателе проявляется единство качественной и количественной сторон. Если не определена качественная сторона явления, нельзя определить и его количественную сторону. Статистика при помощи стат. показателей характеризует: размеры изучаемых явлений; их особенность; закономерности развития; их взаимосвязи. Статистические показатели подразделяются на учетно – оценочные и аналитические. Учетно – оценочные показатели отражают объем или уровень изучаемого явления. Аналитические показатели используются для характеристики особенностей развития явления, распространенности в пространстве, соотношения его частей, взаимосвязи другими явлениями. В качестве аналитических показателей используются: средние величины, показатели структуры, вариации, динамики, степени тесноты и др. Вариация - это многообразие, изменяемость величины признака у отдельных единиц совокупности наблюдения. Вариация признака - пол - мужской, женский. Вариация з/п - 10000, 100000, 1000000. Отдельные значения признака называются вариантами этого признака. Каждое отдельное явление, подлежащее статистическому изучению, называется
Стадии статистического наблюдения. Статистическое наблюдение. Цели и задачи статистического наблюдения. Основные понятия. Статистическое наблюдение – это сбор необходимых данных по явлениям, процессам общественной жизни. Любое статистическое исследование состоит из следующих этапов: · Статистическое наблюдение – сбор данных об изучаемом явлении. · Сводка и группировка – подсчет итогов в целом или по группам. · Получение обобщающих показателей и их анализ (выводы). Задачей статистического наблюдения является получение достоверной исходной информации и получение ее в возможно короткий срок. Стоящие перед менеджером задачи определяют цель наблюдения. Она может вытекать из постановлений правительственных органов, администрации региона, маркетинговой стратегии фирмы. Общая цель статистического наблюдения состоит в информационном обеспечении управления. Она конкретизируется в зависимости от многих условий. Объект наблюдения – совокупность единиц изучаемых явлений, о котором должны быть собраны данные. Единица наблюдения – тот элемент объекта, который обладает изучаемым признаком. Признаки могут быть:
Для регистрации собранных данных используется формуляр – специально подготовленный бланк, имеющий обычно титульную, адресную и содержательную части. В титульной части содержится наименование обследования, организация, проводящая обследование, и кем и когда утвержден формуляр. Адресная часть содержит наименование, местонахождение объекта исследования и др. реквизиты, позволяющие его идентифицировать. В зависимости от построения содержательной части различают два вида формуляра: § Бланк-карточка, который составляется на каждую единицу наблюдения; § Бланк-список, который составляется на группу единиц наблюдения. У каждого из формуляров есть свои достоинства и недостатки. Бланк-карточка удобен для ручной обработки, но связан с дополнительными затратами в оформлении титульной и адресной книги. Бланк-список применяется для автоматической обработки и экономий затрат на подготовку титульной и адресной частей. Для сокращения затрат на сводку и ввод данных целесообразно использовать машины, читающие формуляры. Вопросы содержательной части формуляра должны быть сформулированы таким образом, чтобы на них можно было получить однозначные, объективные ответы. Лучший вопрос это тот, на который можно ответить «Да» или «Нет». Нельзя включать в формуляр вопросы, на которые трудно или нежелательно отвечать. Нельзя соединять в одной формулировке два разных вопроса. Для оказания помощи опрашиваемых в правильном понимании программы и отдельных вопросов составляются инструкции. Они могут быть как на бланке формуляра, так и в виде отдельной книги. Чтобы направить ответы респондента в правильное русло применяются статистические подсказы, то есть готовые варианты ответов. Они бывают полные и неполные. Неполные дают респонденту возможность для импровизации.
Статистические таблицы. Подлежащее и сказуемое таблицы. Простые (перечневые, территориальные, хронологические), групповые и комбинированные таблицы. Простая и сложная разработка сказуемого статистической таблицы. Правила построения таблиц в статистике. Результаты сводки и группировки должны быть представлены так, чтобы ими можно было пользоваться. Существует 3 способа представления данных: 1. данные могут быть включены в текст. 2. представление в таблицах. 3. графический способ Статистическая таблица – система строк и столбцов, в которой в определенной последовательности излагается статистическая информация о социально-экономических явлениях. Различают подлежащее и сказуемое таблицы. Подлежащим называется объект характеризующийся числами, обычно подлежащее дается в левой части таблицы. Сказуемое – система показателей с помощью которых характеризуется объект. Общий заголовок должен отражать содержание всей таблицы, располагается над таблицей по центру. Правило составления таблиц. 1. по возможности таблицу следует составлять небольшой по размеру, легко обозримой 2. общий заголовок таблицы должен кратко выражать по размеру ее осн. содержание (территория, дата) 3. нумерация граф и строк (подлежащего), которые заполняются данными 4. при заполнении таблиц нужно использовать условные обозначения 5. соблюдение правил округления чисел. Статистические таблицы делятся на 3 вида: 1. простые таблицы не содержат в подлежащем систематизации изучаемых единиц статистической совокупности, а содержит перечислений единиц изучаемой совокупности. По характеру представляемого материало эти таблицы бывают перечневые, территориальные и хронологические. Таблицы, в подлежащем которых приводится перечень территории (районов, областей и т.п.), называются перечневыми территориальными. 2. групповые статистические таблицы дают более информативный материал для анализа изучаемых явлений благодаря образованным в их подлежащем группам по существенному признаку или выявлению связи между рядом показателей. 3. при построении комбинационных таблиц каждая группа подлежащего, сформированная по одному признаку, делится на подгруппы по второму признаку, каждая вторая группа делится по третьему признаку, т.е. факторные признаки в данном случае берутся в определенном сочетании, комбинации. Комбинационная таблица устанавливает взаимное действие на результативные признаки и существенную связь связь между факторными группировки. В зависимости от задачи исследования и характера исходной информации сказуемое статистических таблиц бывает простым и сложным. Показатели сказуемого при простой разработке располагаются последовательно один за другим. Распределяя показатели на группе по одному или нескольким признаком в определенном сочетании, получают сложное сказуемое.
Статистические графики. Элементы статистического графика: графический образ, поле графика, пространственные ориентиры, масштабные ориентиры, экспликация графика. Виды графиков по форме графического образу и по образу построения. Статистический гафик – представляет собой чертеж, на котором при помощи условных геометрических фигур (линий, точек или др. символических знаков) изображаются статистические данные. Основные элементы статистического графика: 1. Поле графика – место, на котором он выполняется. 2. Графический образ – это символические знаки, с помощью которых изображаются стат. данные (точки, линии, квадраты, груги и т.д.) 3. Пространственные ориентиры определяют размещение графических образов на поле графика. Они задаются координатной сеткой или контурными линиями и делят поле графика на части, соответствие значениям изучаемых показателей. 4. Масштабные ориентиры стат. графика придают графическим образам количественную значимость, которая передается с помощью системы масштабных шкал. Масштаб графика – это мера перевода численной величины в графическую. Масштабная шкала – линия, отдельной точки которой читаются как определенного числа. Шкала графика может быть прямолинейной и криволинейной, равномерной и неравномерной. 5. Эксплуатация графика – это пояснение его содержания, включает в себя заголовокграфика, объеснение масштабных шкал, пояснения отдельных элементов графического образа. Заголовок графика в краткой и четкой форме поясняет основное содержание изображаемых данных. Также на графике дается текст, делающий возможным чтение графика. Цифровые обозначения шкалы дополняются указанием единиц измерения. Классификация графиков: По способу построения: 1. диаграмма представляет чертеж на котором стат. информация изображается посредством геометрических фигур или символических знаков. В стат. применяют след. виды диаграмм: § линейные § столбиковые § ленточные (полосовые) графики § круговые § радиальные 2. Картограмма – это схематическая (контурная) карта, или план местности, на которой отдельные территории в зависимости от величины изображаемого показателя обозначаются с помощью графических символов (штриховки, расцветки, точек). Картограмма подразделяется на: § Фоновые § Точечные В фоновых картограммах территории с различной величиной изучаемого показателя имеют различную штриховку. В точечных картограммах в качестве графического знака используются точки одинакого размера, размещенные в пределах определенных территориальных единиц. 3. Картодиаграммы (стат. карты) представляет собой сочетание контурной карты (плана) местности с диаграммой. По форме применяемых графических образов: 1. В точечных графиках в качестве граф. образов применяется совокупность точек. 2. В линейных графиках граф. образами являются линии. 3. Для плоскостных графиков граф. образами являются геометрические фигуры: прямоугольники, квадраты, окружности. 4. Фигурные графики. По характеру решаемых задач графики: Рядов распределения; структуры стат. совокупности; рядов динамики; показателей связи; показателей выполнения заданий.
Вариация признака. Абсолютные показатели вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение. Относительные показатели вариации: коэффициенты осцилляции и вариации. Показатели варьирования осредненных статичтических признаков: размах вариации, среднее линейное отклонение, среднее кватратическое отклонение (дисперсия), коэффициент вариации. Расчетные формулы и порядок расчета показателей вариации. Применение показателей вариации при анализе статистических данных в деятельности предприятий и организаций, учреждений БР, макроэкономических показателей. Средний показатель дает обобщающий, типичный уровень признака, но не показывает степень его колеблемости, вариации. Поэтому средние показатели необходимо дополнять показателями вариации. От размера и распределения от клонений зависит надежность средних показателей. Важно знать основные показатели вариации, уметь правильно их рассчитывать и использовать. Основными показателями вариации являются: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Формулы показателей вариации: 1. размах вариации.
Xμαχ - максимальное значение признака Xmin - минимальное значение признака. Размах вариации может служить лишь приближенной мерой вариации признака, т.к. он исчисляется на основе двух крайних ее значений, а остальные во внимание не принимаются; при этом крайние значения признака для данной совокупности могут быть чисто случайными. 2. среднее линейное отклонение.
[X-X] - означает, что отклонения берутся без учета их знака. Среднее линейное отклонение довольно редко используется в экономическом статистическом анализе. 3. Дисперсия.
4. Среднее квадратическое отклонение.
Индексный метод сравнения сложных совокупностей и его элементы: индексируемая величина и соизмеритель (вес). Статистический индекс. Классификация индексов по объекту исследования: индексы цен, физического объема, себестоимости и производительности труда. Слово «индекс» имеет несколько значений: -показатель, -указатель, -опись и т.д. Это слово, как понятие, используют в математике, экономике и др. науках. В статистике под индексом понимается относительный показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве. С помощью индексов решаются следующие задачи: 1. Измерение динамики, социально-экономического явления за 2 и более периода времени. 2. Измерение динамики среднего экономического показателя. 3. Измерение соотношения показателей по разным регионам. По объекту исследования индексы бывают: -производительности труда -себестоимости -цены -физического объема продукции и т.д. 1. индекс цен показывает как изменилась цена в текущем периоде по сравнению с базисным. P1- цена единицы товара в текущем периоде P0- цена единицы товара в базисном периоде 2. индекс физического объема показывает как изменился объем продукции в текущем периоде по сравнению с базисным q1- кол-во проданного или произведеннго товара в текущем периоде q0-кол-во проданного или произведенного товара в базисном периоде 3. индекс себестоимости показывает, как изменилась себестоимость единицы продукции в текущем периоде по сравнению с базисным. Z1- себестоимость единицы продукции в текущем периоде Z0- себестоимость единицы продукции в базисном периоде 4. индекс производительности труда показывает, как изменилась производительность труда одного работающего в текущем периоде по сравнению с базисным периодом t0- трудоемкость обного работающего за базисный период t1- трудоемкость одного работающего за текущий период
По методу отбора -повторный -бесповторный вид выборки При повторной выборке общая численность единиц генеральной совокупности в процессе выборки неизменна. Единицу, попавшую в выборку после регистрации снова возвращают в генеральную совокупность- «отбор по схеме возвращенного шара». Повторная выборка в социально-экономической жизни встречается редко. Обычно выборку организуют по схеме бесповторной выборки. При бесповторной выборке единица совокупности, попавшая в выборку в генеральную совокупность возвращается и в дальнейшем в выборке не участвует (отбор по схеме невозвращенного шара). Т.о., при бесповторной выборки численность единиц генеральной совокупности сокращается в процессе исследования. 3. по степени охвата единиц совокупности: -большие выборки -малые выборки(малая выборка (n<20)) Малая выборка в статистике. Под малой выборкой понимается несплошное статистическое обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Объем малой выборки обычно не превышает 30 единиц и может доходить до 4-5 единиц. В торговле к малой выборке прибегают, когда большая выборка или невозможна, или нецелесообразна (например, если проведение исследования связано с порчей или уничтожением обследуемых образцов). Величина ошибки малой выборки определяется по формулам, отличным от формул выборочного наблюдения со сравнительно большим объемом выборки(n>100). Средняя ошибка малой выборки вычисляется по формуле:
Предельная ошибка малой выборки определяется по формуле:
μ- средняя ошибка выборки. При этом значение коэффициента доверия t зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n. Посредством малой выборки в торговле решается ряд практических задач, прежде всего установление предела, в котором находится генеральная средняя изучаемого признака.
Выборочное наблюдение. Генеральная и выборочная совокупности. Ошибки регистрации и репрезентативности. Ошибка выборочного наблюдения. Средняя и предельная ошибки выборки. Распространение результатов выборочного наблюдения на генеральную совокупность. При любых статичтических исследованиях воз0никают ошибки двух видов: 1. ошибки регистрации могут иметь случайный(непреднамеренный) и ситематический (тендециозный) характер. Случайные ошибки обычно уравновешивают друг друга, поскольку не имеют преимущественного нарпавления в сторону преувеличения или преуменьшения значения изучаемого признака. Систематические ошибки направлены в одну сторону вследствие преднамеренного нарушения правил отбора. Их можно избежать при правильной организации и проведении наблюдения. 2. Ошибки репрезентативности присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Символы:
N- генеральная совокупность
генеральная средняя выборочная средняя
генеральная доля- доля единиц, обладающих данным значением признака
выборочная доля
генеральная дисперсия генеральное среднее квадратическое отклонение выборочная дисперсия выборочное среднее квадратическое оттклонение При выборочном наблюдении должна быть обеспечена случайность отбора единиц.
Для характеристике надежности выборочных показателей различают среднюю и предельную ошибку выборки. 1. средняя ошибка выборки при повотрном отборе 2.
средняя ошибка выборочной доли 3. средняя ошибка при бесповторном отборе
отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки: μ- средняя ошибка выборки t- коэффициент доверия, зависящий от выроятности (P), с которой предельная ошибка определяется. Для повторного отбора предельная ошибка равна: Для бесповторного отбора предельная ошибка равна:
Для доли предельная ошибка при повотрном отборе равна:
Значение интеграла Лапласа- это вероятность (P) для разных tприведены в специальной таблице: при t=1 P=0.683 при t=2 P=0.954 при t=3 P=0.997 Это означает, что с вероятностью 0,683 можно гарантировать, что отклонение генеральной средней от выборочной не превысит однократной средней ошибки Причинно-следственные связи между явлениями. Этапы изучения причинно-следственнных связей: качественный анализ, построение модели связи, интерпретация результатов. Функциональная связь и стохастическая зависимость. Исследование объективно существующих связей между явлениями - важнейшая задача теории статистики. В процессе статистического исследования зависимостей вскрываются причинно -следственные отношения между явлениями, что позволяет выявлять факторы (признаки),
оказывающие основное влияние на вариацию изучаемых явлений и процессов. Причинно -следственные отношения - это такая связь явлений и процессов, когда изменение одного из них - причины ведет к изменению другого - следствия. Признаки по их значению для изучения взаимосвязи делятся на два класса. Признаки, обуславливающие изменения других, связанных с ними признаков, называют факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, называют результативными. Понятие о взаимосвязи между различными признаками изучаемых явлений. Признаки-факторы и результативные признаки. Виды взаимосвязи: функциональная и корреляционная. Поле корреляции. Прямая и обратная связь. Линейные и нелинейные связи. Прямые и обратные связи. В зависимости от направления действия функциональные и стохастические связи могут быть прямыми и обратными. При прямой связи направление изменения результативного признака совапдает с направлением изменения признака-фактора, т.е. с увеличением факторного признака увеличивается и результативный, и, наоборот, с уменьшением факторного признака уменьшается и результативный признак. В противном случае между рассматриваемыми величинами существуют обратные связи. Например, чем выше квалификация рабочего (разряд), тем выше уровень производительности труда- прямая связь. А чем выше производительность труда, тем ниже себестоимость единицы продукции- обратная связь. Прямолинейные и криволинейные связи. По аналитическому выражению (форме) связи могут быть прямолинейными и криволинейными. При прямолинейной связи с возрастанием значения факторного признака происходит непрерывное возрастание (или убывание) значений результативного признака. Математически такая связь представляется уравнением прямой, а графически прямой линией. Отсюда ее более короткое название- линейная связь. При криволинейных связях свозрастанием значения факторного признака возрастание (или убывание) результативного признака происходит неравномерно или же направление его измененияменяется на обратное. Геометрически такие связи представляются кривыми линиями (гиперболой, параболой и т.д.). Предмет и задачи статистики. Закон больших чисел. Основные категории статистической методологии. В настоящее время термин «статистика» употребляется в 3х значениях: · Под «статистикой» понимают отрасль деятельности, к-рая занимается сбором, обработкой, анализом, публикаций данных о различных явлениях общественной жизни. · Статистикой называют цифровой материал, служащий для характеристики общих явлений. · Статистикой называют отрасль знания, учебный предмет. Предметом статистики является количественная сторона массовых общих явлений в неразрывной связи с их качественной стороной. Свой предмет статистика изучает при помощи опр. категорий: · Статистическая совокупность – совокупность соц.-эк. объектов и явлений общ. Жизни, объединен. Некоторой кач. Основой н-р, совокупность пред-тий, фирм, семей. · Единица совокупности – первичный элемент статистической совокупности. · Признак – кач. Особенность единицы совокупности. · Статистический показатель – понятие отбражает количеств. харак-ки (размеры) признаков общ. явлений. · Система статистич. Показателей – совокупность статистич. показателей, отражающая взаимосвязи, к-рые существ. между явлениями. Основными задачами статистики являются: 1. всестороннее исследование глубоких преобразований эк. и соц. процессов на основе научнообоснов. системы показателей. 2. обобщение и прогнозирование тенденций развития разл. отраслей экономики в целом 3. своевременное обеспеч. надежности информации гос., хоз., эк. органов и широкой общ-сти
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 3692; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.017 с.) |



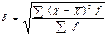
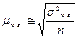
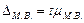
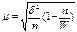
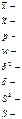 n- объем выборки
n- объем выборки