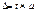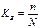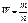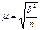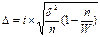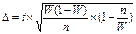Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборочное наблюдение. Генеральная и выборочная совокупности. Виды выборки: собственно-случайная, механическая, типическая, серийная, комбинированная.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В статистике различают следующие виды выборок: 1. Собственно случайная выборка, суть которой состоит в том, что отбирают единицы по жребию. Отбор осуществляется повторный и бесповторный. Повторный отбор, при котором единицы совокупности участвуют столько раз, сколько происходит наблюдение. Бесповторный отбор - единица, выбранная раз, больше не участвует. 2. Механическая выборка. Генеральную совокупность механически разбивают на столько частей, сколько надо отобрать в выборку, а затем из каждой части механически отбирают единицы. Механическая выборка производится только бесповторным способом. 3. Типическая выборка. Генеральная совокупность также разбивается на группы, но обязательно по какому-то признаку, а затем из каждой группы случайным или механическим способом отбирают нужное число единиц. 4. Серийная. Отбирают не отдельные единицы, а целые группы или серии. Затем обследуют все единицы отобранных групп. Способ отбора случайный, либо механический, но бесповторным способом. 5. Многоступенчатая выборка. Типически отобранная часть сочетается с несколькими стадиями или ступенями отбора, причем на каждой ступени выбирается своя единица. 6. Многоразовая. Сохраняется одна и та же единица совокупности. 7. Комбинированная. Выборочное наблюдение сочетается со сплошным. 8. Моментное наблюдение. Фиксируются не единицы совокупности, а состояние явления. 9. Малая выборка. Число единиц до 20. Малая выборка в статистике. Под малой выборкой понимается несплошное статистическое обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Объем малой выборки обычно не превышает 30 единиц и может доходить до 4-5 единиц. В торговле к малой выборке прибегают, когда большая выборка или невозможна, или нецелесообразна (например, если проведение исследования связано с порчей или уничтожением обследуемых образцов). Величина ошибки малой выборки определяется по формулам, отличным от формул выборочного наблюдения со сравнительно большим объемом выборки(n>100). Средняя ошибка малой выборки вычисляется по формуле:
Предельная ошибка малой выборки определяется по формуле:
μ- средняя ошибка выборки. При этом значение коэффициента доверия t зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n. Посредством малой выборки в торговле решается ряд практических задач, прежде всего установление предела, в котором находится генеральная средняя изучаемого признака.
Выборочное наблюдение. Генеральная и выборочная совокупности. Ошибки регистрации и репрезентативности. Ошибка выборочного наблюдения. Средняя и предельная ошибки выборки. Распространение результатов выборочного наблюдения на генеральную совокупность. При любых статичтических исследованиях воз0никают ошибки двух видов: 1. ошибки регистрации могут иметь случайный(непреднамеренный) и ситематический (тендециозный) характер. Случайные ошибки обычно уравновешивают друг друга, поскольку не имеют преимущественного нарпавления в сторону преувеличения или преуменьшения значения изучаемого признака. Систематические ошибки направлены в одну сторону вследствие преднамеренного нарушения правил отбора. Их можно избежать при правильной организации и проведении наблюдения. 2. Ошибки репрезентативности присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Символы:
N- генеральная совокупность
генеральная средняя выборочная средняя
генеральная доля- доля единиц, обладающих данным значением признака
выборочная доля
генеральная дисперсия генеральное среднее квадратическое отклонение выборочная дисперсия выборочное среднее квадратическое оттклонение При выборочном наблюдении должна быть обеспечена случайность отбора единиц.
Для характеристике надежности выборочных показателей различают среднюю и предельную ошибку выборки. 1. средняя ошибка выборки при повотрном отборе 2.
средняя ошибка выборочной доли 3. средняя ошибка при бесповторном отборе
отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки: μ- средняя ошибка выборки t- коэффициент доверия, зависящий от выроятности (P), с которой предельная ошибка определяется. Для повторного отбора предельная ошибка равна: Для бесповторного отбора предельная ошибка равна:
Для доли предельная ошибка при повотрном отборе равна:
Значение интеграла Лапласа- это вероятность (P) для разных tприведены в специальной таблице: при t=1 P=0.683 при t=2 P=0.954 при t=3 P=0.997 Это означает, что с вероятностью 0,683 можно гарантировать, что отклонение генеральной средней от выборочной не превысит однократной средней ошибки
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 988; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.120 (0.007 с.) |

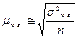
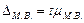
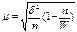
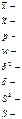 n- объем выборки
n- объем выборки