
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 8. Выборочное наблюдениеСодержание книги
Поиск на нашем сайте
Сущность генеральной и выборочной совокупности В статистике нечасто встречается сплошной вид наблюдения, каким является, например, всеобщая перепись населения. Чаще приходится использовать несплошные наблюдения, когда из совокупности необходимо выбирать какую-то часть единиц и на основании ее обследования давать характеристику всем статистическим единицам совокупности. В связи с этим целесообразно отметить, что все показатели качества продукции, например, содержание белков, жиров, углеводов, минеральных веществ, витаминов в продуктах питания, могут быть получены только в результате выборочных наблюдений. В статистике используются ключевые понятия: генеральная и выборочная совокупность. Генеральной совокупностью следует считать весь комплекс реально существующих объектов, которые теоретически могут быть охвачены статистическим наблюдением. Синонимами этого понятия являются: вероятностное пространство, случайная величина и закон распределения вероятностей. Генеральная совокупность может быть как конечной, так и бесконечной. Выборочная совокупность – это комплекс статистических единиц, отобранных по определенным правилам из генеральной совокупности статистического наблюдения. Главное требование, предъявляемое к выборочной совокупности, заключается в максимальном приближении ее основных статистических характеристик (средней, дисперсии, среднего квадратического отклонения, коэффициента вариации и т.д.) к соответствующим характеристикам генеральной совокупности, т.е. между основными характеристиками должна быть минимальная разница, которую принято называть ошибкой представительности (репрезентативности). Это означает, что выборочная совокупность призвана надежно представлять (замещать)генеральную совокупность. Полученные в результате выборочных наблюдений статистические характеристики целесообразно оценить на соответствие результатам, ожидаемым по генеральной совокупности. Выборочные данные должны представлять или, как говорят статистики, репрезентатировать не выборочную, а генеральную совокупность. Условие репрезентативности будет выполнено, если выборочная совокупность отразит в миниатюре генеральную совокупность. Выборочная совокупность должна быть частицей генеральной совокупности, имея в виду, что частица – это не часть, а целое, копия в миниатюре, так как часть не может характеризовать собою целое. Именно формирование не части, а частицы, т.е. миниатюрной копии генеральной совокупности исключает преднамеренный отбор единиц в составе выборочной совокупности.
Сущность выборочного метода
Статистическая работа в большинстве случаев так или иначе связана с данными, полученными в результате применения выборочного метода. Многие исследования были бы невыполнимы, если бы не использовались материалы выборочных наблюдений. Так, для оценки качества сельскохозяйственной продукции (зерна, льнотресты, картофеля, кормов, молока, продукции выращивания животных и т.д.) нет никакой необходимости исследовать весь объем валового производства. Для этого из общего объема каждого вида продукции достаточно взять несколько небольших проб. Например, при определении жирности молока во время его реализации в перерабатывающую организацию из каждой фляги обычно берут для анализа стограммовую навеску. Выборочный – метод статистического наблюдения, которое дает характеристику генеральной статистической совокупности на основании обследования некоторой ее части. Выборочное наблюдение достигает цели только при условии соблюдения принципов и правил отбора статистических единиц, исключающих субъективность и тенденциозность. Если выборочное наблюдение проведено с соблюдением всех правил научной его организации, то результаты выборки объективно характеризуют генеральную совокупность. Практика применения выборочного метода доказывает, что статистические характеристики, полученные в результате выборочного наблюдения, близки к характеристикам сплошного наблюдения. Как генеральная, так и выборочная совокупности характеризуются своими показателями: средним размером признака, дисперсией, средним квадратическим отклонением, коэффициентом вариации изучаемого признака, долей и другими статистическими характеристиками. Для формального различия между генеральными и выборочными статистическими характеристиками обычно используется специальная символика. Например, если генеральную среднюю обозначают, скажем, через Массовые явления, изучаемые статистикой, связаны с большим числом случайных воздействий на них, и случайные отклонения основных статистических характеристик выборочной и генеральной совокупностей могут быть минимальны, а результаты выборочного наблюдения достоверны при условии, если отбираются достаточно большое число статистических единиц. Основное свойство выборочного метода заключается в том, что если численность выборки достаточно велика, то выборочные характеристики достаточно хорошо воспроизводят генеральные характеристики. Поэтому они играют важную роль в обосновании выборочного наблюдения. При массовом наблюдении распределение эмпирических частот в дискретном или интервальном вариационном ряду подчиняется закону нормального распределения. Так, если графически изобразить ряд распределения в форме полигона или гистограммы, то можно заметить, что эти диаграммы очень близко воспроизводят кривую, отображающую закон нормального распределения. Нормальное распределение показывает, что большая часть вариант статистической совокупности сосредоточена ближе к генеральной средней. Теоретически обосновано и практически доказано, что около 68,3 % численности выборочных вариант не выходит за пределы ± Выборочный метод имеет ряд преимуществ перед сплошным наблюдением. Во-первых, выборочное наблюдение позволяет существенно экономить труд, средства, время для его проведения. Совершенно очевидно, что статистическое наблюдение по одной и той же программе, например, 100 единиц требует меньше и времени, и труда, и средств, чем статистическое обследование 1000 единиц. Кроме экономии на охвате меньшего числа статистических единиц, прибавляется и экономия, достигаемая при проведении статистической обработки материалов наблюдения, поскольку ей подлежит меньший объем информации. Во-вторых, выборочное наблюдение позволяет достигать большей глубины, детальности и точности регистрации фактов. Применение выборочного метода расширяет возможности ввода в программу наблюдения дополнительных вопросов, чем и достигается детальность и, следовательно, большая глубина регистрации. Повышенная точность результатов наблюдения объективно может быть достигнута за счет существенного уменьшения случайных ошибок, количество которых пропорционально численности статистических единиц. В-третьих; выборочный метод обычно применяют в тех случаях, когда сплошное наблюдение из-за его громоздкости нецелесообразно. Понятно, что под ним понимается слишком большой объем работы, неоправданно растянутые сроки, привлечение значительного числа дополнительных квалифицированных работников и т.д. Учитывая эту позицию, выборочное наблюдение применяют, например, при проведении постоянных бюджетных обследованиях домашних хозяйств, регистрации цен на рынках, изучении потребительского рынка, решении вопросов «теневой» экономики и др. В-четвертых, выборочный метод используют в тех случаях, когда сплошное наблюдение невозможно. Это относится главным образом к статистическим наблюдениям за качеством продукции, изделий и неизбежно связано с их порчей или разрушением. Например, взятые пробы, предназначенные для определения качества молочных продуктов в перерабатывающих организациях, после завершения химического анализа, естественно, непригодны для потребления. Исследование льнотресты, льноволокна на прочность связано с их разрушением. Перечисленные существенные преимущества выборочного метода "уравновешиваются" значительным недостатком. Дело в том, что распространение результатов выборки на генеральную совокупность неизбежно связано с погрешностью, которую принято называть ошибкой репрезентативности. Эта ошибка формируется вследствие факта неполного охвата всех единиц в генеральной совокупности. Безупречное выборочное наблюдение не гарантирует абсолютной точности представления генеральной совокупности. Тем не менее многократное практическое выборочное наблюдение и сопоставление его результатов с данными сплошного обследования одного и того же объекта, например, при переписи населения показывает, что основные выборочные характеристики в достаточной мере воспроизводят соответствующие характеристики генеральной статистической совокупности. Теория и практика выборочного метода получила углубленное обоснование и развитие в фундаментальных работах выдающихся русских математиков: П.Д.Чебышева, А.Ляпунова, А.А.Маркова и др. В их трудах разработаны основные положения теории выборочного метода.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.219.11 (0.007 с.) |

 , то аналогичную выборочную среднюю – через
, то аналогичную выборочную среднюю – через 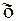 ; генеральную дисперсию –
; генеральную дисперсию – 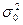 , выборочную – соответственно
, выборочную – соответственно  . В генеральной совокупности доля единиц, обладающих тем или иным признаком, называется генеральной долей, которую можно обозначить через Р. В свою очередь выборочная доля обозначается через d.
. В генеральной совокупности доля единиц, обладающих тем или иным признаком, называется генеральной долей, которую можно обозначить через Р. В свою очередь выборочная доля обозначается через d.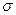 генеральной средней; 95,4 % этой численности заключено в пределах ± 2
генеральной средней; 95,4 % этой численности заключено в пределах ± 2 


