
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение прямолинейной регрессииСодержание книги
Поиск на нашем сайте
Корреляционную связь в форме, близкой к прямолинейной, можно представить в виде уравнения прямой линии:
где В уравнении 9.8 параметр Для нахождения параметров
При расчете искомых параметров
Т а б л и ц а 11.5. Вспомогательные расчеты для определения параметров уравнения прямолинейной связи
Таким образом, для решения системы нормальных уравнений (11.9 и 11.10) необходимо найти значения Σх, Σу, Σху и Σх2. Допустим, необходимо определить, как изменяется в среднем урожайность рапса в зависимости от колебания доз минеральных удобрений по данным статистической совокупности из 30 сельскохозяйственных организаций, если известно, что дозы удобрений колеблются в пределах от 56 до 183 кг действующего вещества на 1 га, а урожайность рапса – от 16,9 до 30,4 ц/га. Для составления уравнения прямолинейной регрессии (11.8) по имеющимся данным необходимо решить систему нормальных уравнений. С этой целью прежде всего составим рабочую табл. 11.6.
Т а б л и ц а 11.6. Вспомогательные расчеты для определения параметров уравнения прямолинейной взаимосвязи
Подставим полученные в табл. 11.6 конкретные значения Σх=3283, Σу=640, Σху=91204 и Σх2=535692 в уравнения 11.9 и 11.10; получим:
Для расчета коэффициента пропорциональности
Вычтем четвертое уравнение из третьего. Получим 21,3 – 27,7 = а+а+109,4в – 163,2 в; - 6,4 = - 53,8 в; в = 0,12. Теперь найдем параметр а, подставив значение в, например, в третье уравнение: 21,3 = а + 109,4. · 0,12; а=8,2. Уравнение прямолинейной регрессии, выражающее зависимость между дозами минеральных удобрений и урожайностью рапса, имеет следующий вид:
Коэффициент пропорциональности в показывает, что повышение доз внесения в почву минеральных удобрений на 1 кг действующего вещества может вызвать прирост урожайности рапса в сельскохозяйственных организациях 12 кг. Это свидетельствует о существенной роли минеральных туков в достижении высоких и устойчивых урожаев сельскохозяйственных культур.
Уравнение гиперболической регрессии Если форма связи между изучаемым признаком-фактором и признаком-результатом, выявленная с помощью координатной диаграммы (поля корреляции), приближается к гиперболической, то необходимо составить и решить уравнение гиперболической регрессии:
где В уравнении (11.12) коэффициент Параметры
Для решения системы уравнений (11.13) и (11.14) в общем виде обычно составляют вспомогательную табл. 11.7.
Т а б л и ц а 11.7. Вспомогательные расчеты для нахождения Гиперболической регрессии
В качестве примера можно взять исходные данные, характеризующие зависимость себестоимости 1 кг меда от продуктивности 1 пчелосемьи по 30 сельскохозяйственным организациям. По этим данным необходимо составить и решить уравнение регрессии между указанными признаками. Себестоимость единицы продукции, представляющая комплекс всех затрат в денежной форме, разделенных на к количество продукции, можно условно расчленить на постоянную и переменную части. При этом постоянная часть расходов не зависит от объема продукции, а переменная – изменяется пропорционально ее количеству. Поэтому изменение себестоимости 1 кг продукции под воздействием продуктивности пчел теоретически можно представить в виде гиперболической регрессии. Графическое изображение зависимости с помощью координатной диаграммы показало, что основная масса точек сосредоточена в форме, близкой к гиперболической. Поэтому для составления и решения системы нормальных уравнений (9.13), (9.14) гиперболической регрессии целесообразно найти значения Т а б л и ц а 11.8. Расчет вспомогательных показателей для уравнения Гиперболической регрессии
Подставим конкретные данные в уравнения (11.13), (11.14) и получим:
Для нахождения параметров
Из третьего уравнения вычтем четвертое. Получим 2,9 а = 4,7; а = 1,62. Значение Уравнение гиперболической регрессии, выражающее зависимость между продуктивностью пчеловодства и себестоимостью меда, имеет следующий вид:
Данные уравнения 11.15 показывают, что параметр
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 413; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.113.24 (0.009 с.) |

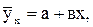 (11.8)
(11.8) – среднее значение результативного признака; х – значение факторного признака;
– среднее значение результативного признака; х – значение факторного признака;  – параметр уравнения, обычно характеризующий минимальное значение результативного признака;
– параметр уравнения, обычно характеризующий минимальное значение результативного признака;  – коэффициент пропорциональности изменения признака-результата.
– коэффициент пропорциональности изменения признака-результата. характеризует среднее значение результативного признака у при элиминировании признака-фактора х, т.е. х=0. Коэффициент в зависимости от знака (+) или (–) показывает пропорциональность изменения результата у, т.е. его приращения или убывания при абсолютном изменении фактора на каждую его единицу.
характеризует среднее значение результативного признака у при элиминировании признака-фактора х, т.е. х=0. Коэффициент в зависимости от знака (+) или (–) показывает пропорциональность изменения результата у, т.е. его приращения или убывания при абсолютном изменении фактора на каждую его единицу. (11.9)
(11.9) (11.10)
(11.10)



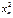


 разделим уравнения 1,2 на числа, находящиеся при
разделим уравнения 1,2 на числа, находящиеся при 
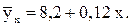 (11.11)
(11.11) (11.12)
(11.12) – среднее значение зависимого результативного признака; х – значение признака-фактора; а – среднее значение признака-результата при условии полной изоляции влияния фактора (х=0);
– среднее значение зависимого результативного признака; х – значение признака-фактора; а – среднее значение признака-результата при условии полной изоляции влияния фактора (х=0); 





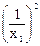








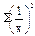
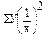
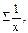 Σу,
Σу, 
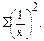 Расчет этих значений приведен в табл. 11.8.
Расчет этих значений приведен в табл. 11.8.


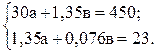

 подставим в первое уравнение. Получим
подставим в первое уравнение. Получим 
 (11.15)
(11.15)


