Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные показатели динамического ряда. Уровень динамического рядаСодержание книги
Поиск на нашем сайте
Всесторонний анализ динамического ряда позволяет вскрывать и характеризовать закономерности, проявляющиеся на разных этапах развития явлений, выявить тенденции и особенности их развития. В процессе анализа динамического ряда используют следующие показатели динамики: уровни ряда, абсолютные приросты уровней, темпы роста, темпы прироста, абсолютные значения одного процента прироста. Исходные значения признака, образующие динамический ряд, называются уровнями ряда. Они служат начальной базой для расчета и оценки различных показателей динамики. В большинстве случаев этот расчет основан на сравнении между собой уровней ряда. Тот уровень, который является базой для сравнения и с которым производится сравнение других уровней, называется базисным. За базу сравнения применяют либо начальный (первый), либо предыдущий, или любой уровень динамического ряда. Базисный уровень в статистике обычно принято обозначать У0. Уровень ряда, который сравнивается с базисным, называется текущим (отчетным). Текущие уровни могут иметь следующие обозначения: У1, У2, У3…Уn. Если все уровни динамического ряда сравниваются с одним и тем же уровнем, то полученные показатели динамики называются базисными. Если же каждый последующий уровень ряда сравнивается с каждым предыдущим, то полученные динамические показатели называются цепными. Эти показатели представляют собой как бы отдельные звенья единой «цепи», связывающей уровни ряда. В динамическом ряду приводится несколько последовательных уровней, среди которых особый интерес представляют начальный, срединный и конечный уровни ряда. Первый член динамического ряда называется начальным уровнем. Срединный уровень ряда находится обычно по способу определения медианы: при нечетном числе уровней срединным считается тот, который находится в середине ряда; при четном – срединный уровень рассчитывают как полусумму из двух смежных уровней, находящихся в средине динамического ряда. Последний член динамического ряда принято называть конечным. Допустим, имеются данные об объеме товарных овощей в административном районе, тыс. тонн: 2006 г. – 20; 2007 г. – 18; 2008 г. – 15; 2009 г. – 19; 2010 г. – 22. В этом динамическом ряду начальным уровнем является объем товарных овощей в 2006 г., срединным – в 2008 г., и конечным – объем товарных овощей в 2010 г.
Для общей характеристики явления за весь период целесообразно рассчитать средний уровень из всех членов динамического ряда. При этом способ расчета среднего уровня зависит от вида динамического ряда. При расчете среднего уровня в моментном динамическом ряду (с равными промежутками между моментами) рекомендуется использовать способ средней хронологической простой величины. Следует обратить внимание на то, что уровней в моментном ряду всегда на единицу больше числа интервальных промежутков между моментами. Например, в каждом квартале, включающем три месяца, число моментов и соответствующих им уровней ряда равно четырем. Соответственно этому моментный ряд за полный год всегда насчитывает пять квартальных или 13 помесячных моментов и столько же уровней. Допустим, необходимо рассчитать среднее поголовье коров за первый квартал года в сельскохозяйственной организации по следующим данным: Дата 1.01 1.02 1.03 1.04 Число голов 800 810 830 840 Приведенные данные показывают, что поголовье коров зафиксировано по состоянию на первое число каждого месяца. При этом предполагается, что с 1.02 по 1.04 поголовье на конец каждого месяца в первом квартале существенно не отличается от поголовья по смежным начальным датам: поголовье на 1.02 ≈ поголовью на 31.01; на 1.03 ≈ на 28 (29). 02 и т.д. Кроме того, что помесячные промежутки между указанными моментами приблизительно равны между собой и составляют один месяц. Предполагается, что изменение численности коров в промежутках между указанными датами шло более-менее равномерно. Следовательно, для расчета среднего квартального поголовья можно воспользоваться формулой хронологической моментного ряда. Подставим в формулу исходные данные и получим:
Таким образом, в сельскохозяйственной организации в среднем за первый квартал имелось 820 коров. В тех случаях, когда моментный ряд динамики представлен неравными промежутками между датами, средний уровень ряда обычно рассчитывают по способу средней арифметической взвешенной, т.е.
где у – постоянные уровни ряда: t – промежутки времени с постоянными уровнями. Пример. Имеются данные о численности работников в фермерском хозяйстве:
Дата 1.08 10.08 17.08 31.08 Численность 12 15 20 12 Необходимо рассчитать среднемесячную численность работников за август. Из приведенных данных видно, что между указанными датами были различные промежутки времени (в днях) и существенно различалась численность работников. Поэтому при определении средней численности работников за весь август необходимо их число за каждый отдельный промежуток взвесить через количество календарных дней, т.е. применить формулу (10.1):
Таким образом, в фермерском хозяйстве в течение августа работало ежедневно в среднем 16,3 работника. При расчете среднего уровня в периодическом ряду динамики обычно рекомендуют использовать способ средней арифметической простой величины, т.е.
где у – уровни периодического ряда; n – число уровней в ряду. Предположим, имеются данные о реализации льнотресты в сельскохозяйственной организации по месяцам четвертого квартала: Месяцы Октябрь Ноябрь Декабрь Объем, т 500 400 300 Необходимо найти среднемесячный объем реализации льнотресты. Для этого воспользуемся формулой (10.2) и получим:
Следовательно, среднемесячная реализация льнотресты в четвертом квартале составила 400 т.
Абсолютные приросты уровней Одним из наиболее простых показателей развития динамики является абсолютный прирост уровня. Абсолютным приростом называется разность двух уровней динамического ряда. Измеряется в тех же единицах, в которых показаны уровни ряда динамики. Если абсолютный прирост уровня обозначим через ΔУ, уровень последующего периода – Уi, предыдущего – Уi-1, то значение абсолютного прироста алгебраически можно выразить так:
где Абсолютный прирост выражает абсолютное изменение уровней и показывает, на сколько единиц увеличился или уменьшился последующий уровень динамического ряда по сравнению с предыдущим. Характер динамического ряда может принимать разнообразные формы. Если уровни ряда от начального к конечному увеличиваются, то такой динамический ряд будет иметь положительные абсолютные приросты. Например, необходимо найти абсолютный прирост государственных закупок сахарной свеклы административного района в 2010 г. по сравнению с 2009 г. по следующим данным (тыс. т), если было закуплено соответственно 145 и 140 тыс. тонн. Абсолютный прирост составил (по формуле (9.3): В тех случаях, когда каждый последующий уровень ряда ниже предыдущего (базисного), имеет место не абсолютный прирост, а абсолютное снижение уровня. Определим абсолютное снижение объема переработки картофеля в перерабатывающей организации в 2010 г. по сравнению с 2008 г., если за этот период переработка снизилась со 100, 1 до 95,3 тыс. т.
Это означает, что объем переработки картофеля уменьшился на 4,8 тыс. тонн. Абсолютные приросты могут быть рассчитаны базисным и цепным способами. Абсолютные приросты, полученные в результате сравнения текущих (отчетных) уровней с постоянными (базисными), называют базисными. Приросты, которые получены при сравнении каждого последующего уровня с предыдущим, называются цепными. Исчислим базисные и цепные абсолютные приросты урожайности картофеля в сельскохозяйственной организации по следующим данным (табл. 9.2).
Т а б л и ц а 9.2. Урожайность картофеля в сельскохозяйственной Организации «Днепр»
Базисные и цепные абсолютные приросты имеют общую для их базу и поэтому связаны между собой следующими зависимостями: • во-первых, сумма n последовательных цепных абсолютных приростов, начиная с первого, равна n-ому базисному абсолютному приросту, т.е. Σ ΔУц=ΔУб. (9.4) • во-вторых, разность между смежными (последующим и предыдущим) базисными абсолютными приростами равна соответствующему цепному абсолютному приросту, т.е.
Приведенная зависимость может быть при необходимости использована для преобразования цепных абсолютных приростов в базисные и наоборот. Например, имеются данные о цепных приростах подекадного объема переработки зерна на мелькомбинате: за 1 декаду –– 10 т, за 2 –– 8 т, за 3 декаду –– 6 т. Необходимо рассчитать базисные абсолютные приросты объема переработки зерна за каждую декаду. Для нахождения базисных абсолютных приростов воспользуемся первой зависимостью по формуле (10.4). В результате получим: базисный абсолютный прирост за первую декаду ΔУ1=0+10=10 т; за вторую –– ΔУ2=10+8=18 т; за третью –– ΔУ3=10+8+6=24 т. Если есть необходимость найти цепные абсолютные приросты по приведенным базисным приростам, то можно воспользоваться второй зависимостью по формуле (10.5). Допустим, имеются данные о базисных абсолютных приростах помесячного объема переработки сахарной свеклы на сахарном комбинате: в ноябре –– 240 тыс. т, в декабре –– 210, в январе –– 220, в феврале –– 150 тыс. т. По этим данным необходимо рассчитать цепные абсолютные приросты помесячного объема переработки сахарной свеклы. Согласно второй зависимости имеем: за ноябрь ΔУ1=240-0=240 тыс. т. за январь ΔУ3=220-210=10 тыс. т. за декабрь ΔУ2=210-240=-30 тыс. т. за февраль ΔУ4=150-220=-70 тыс. т.
В статистико-экономических исследованиях часто приходится рассчитывать средний абсолютный прирост уровней динамического ряда. Средний абсолютный прирост всегда является периодическим показателем. Поэтому он исчисляется по формуле простой средней арифметической из цепных абсолютных приростов за последовательные и более-менее равные по продолжительности периоды:
где: Пример. Определить среднемесячный абсолютный прирост объема переработки молока в перерабатывающей организации за первый квартал (табл. 10.3).
Т а б л и ц а 9. 3. Объем переработки молока
Используя формулу (10.6), находим среднемесячный абсолютный прирост переработки молока:
Согласно первой зависимости общая сумма цепных абсолютных приростов (Σ ΔУц) ряда динамики представляет собой базисный абсолютный прирост за весь изучаемый период в целом (Уn – У0). Число приростов (n) равно числу уровней ряда минус единица
где Уп – значение конечного уровня динамического ряда; У0 – начальный уровень ряда; Пример. Найти среднегодовой абсолютный прирост валового сбора фруктов и ягод в специализированной сельскохозяйственной организации за период 2008 – 2010 гг., если известно, что в 2008 г. было собрано 1596 т, а в 2010 г. – 1823 т. Расчет среднегодового абсолютного прироста ведем по формуле (10.6), т.е. Следовательно, за изучаемый период среднегодовой абсолютный прирост валового сбора фруктов и ягод составил 113,5 т.
Темпы роста уровней Для характеристики относительной скорости изменения уровня динамического ряда используется показатель темпа роста. Это выраженное в процентах отношение одного уровня динамического ряда к другому, принятому за базу сравнения. Темпы роста могут быть выражены в форме коэффициентов или процентов. Коэффициент роста показывает, во сколько раз сравниваемый (текущий) уровень больше базисного:
где К – коэффициент роста уровней; Уi – уровень последующего периода; Уi-1 – уровень предыдущего периода. Коэффициент роста, выраженный в процентах, называется темпом:
Пример. Валовая продукция маслосырзавода в 2010 г. составила 32,0 млрд. рублей, в 2009 г. – 30,7 млрд. рублей. Необходимо найти темп роста валовой продукции в 2010 г. по сравнению с 2009 г. Для решения воспользуются формулами (10.8 и 10.9). Во-первых,
Следовательно, производство валовой продукции маслосырзавода в 2010 г. увеличилось по сравнению с 2009 г. в 1,042 раза. Во-вторых, Это означает, что объем валовой продукции в 2010 г. составил 104,2 % объема продукции 2009 года. Темпы роста могут быть рассчитаны базисным и цепным способами. Допустим, необходимо исчислить базисные и цепные темпы роста урожайности картофеля в сельскохозяйственной организации «Днепр» (табл. 9.4).
Т а б л и ц а 9.4. Динамика урожайности картофеля в сельскохозяйственной Организации
Между базисными и цепными темпами роста, выраженными в форме коэффициентов, имеется определенная взаимосвязь, которая заключается в следующем: • во-первых, произведение последовательных цепных темпов роста равно базисному темпу роста за соответствующий период;
• во-вторых, частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста. Указанные зависимости между темпами роста можно использовать для преобразования базисных темпов в цепные и наоборот, особенно в тех случаях, когда неизвестны абсолютные уровни динамики. Пример. Известно, что производительность труда в фермерском хозяйстве в 2010 г. возросла по сравнению с 2006 г. в 1,2 раза, а в 2006г. по сравнению с 2002 г. – в 1,3 раза. Необходимо определить, как повысилась производительность труда в 2010 г. по сравнению с 2002 г., т.е. найти темп роста производительности труда за период 2002 – 2010 гг. С этой целью рассуждаем так: поскольку коэффициенты роста за первый и второй периоды –– цепные, то базисный коэффициент за весь промежуток времени равен их произведению, т.е. Кб=1,2 · 1,3=1,56. Это означает, что базисный темп роста составил 156 %, т.е. в 2010 г. производительность труда в фермерском хозяйстве повысилась по сравнению с 2002 г. в 1,56 раза (156 %). Темпы роста уровней динамического ряда по отдельным периодам, как правило, неодинаковы и обнаруживают некоторые колебания. Вследствие этого обычно возникает необходимость исчисления среднего темпа роста уровней за весь изучаемый период. В отличие от абсолютного прироста за весь период, который представляет собой сумму абсолютных приростов за каждый отдельный промежуток времени, общий показатель темпа роста –– это произведение цепных коэффициентов (темпов) роста за каждый промежуток времени, т.е. коэффициенты связаны между собой знаком произведения. Поэтому для определения среднего темпа роста необходимо применить среднюю геометрическую простую, т.е.
где Например, валовая продукция в сельскохозяйственной организации «Днепр» за период 2008 – 2010 г. имела следующие коэффициенты роста: 2008 г. – 1,09; 2009 – 1,02; 2010 – 1,04 раза. По этим данным необходимо найти среднегодовой темп роста валовой продукции. Применим для решения формулу (9.10) и получим Если произведение цепных темпов заменить соответствующим базисным темпом роста за весь изучаемый период, то получим формулу среднего темпа роста:
где Применение формулы (9.11) по сравнению с предыдущей (9.10) позволяет значительно упростить расчет среднего темпа роста. Кроме того, формулой (9.11) можно пользоваться в тех случаях, когда имеются значения только начального и конечного уровней. Допустим, необходимо определить среднегодовой темп роста площади пахотных земель в фермерском хозяйстве за период 2001 – 2010 гг., если в начале этого периода фермер имел 10 га, а в конце –– 100 га земель. Расчет искомого среднегодового темпа роста ведем по формуле (9.11), т.е.
Следовательно, ежегодный темп роста площади пахотных земель в фермерском хозяйстве в среднем составлял 129,2 %.
Темпы прироста уровней Если абсолютная скорость прироста уровней динамического ряда характеризуется величиной абсолютных приростов, то относительная скорость прироста уровней – темпами прироста. Темп прироста представляет собой отношение абсолютного прироста к уровню, принятому за базу. Темпы прироста, как и темпы роста, могут быть выражены в форме коэффициентов и процентов. Коэффициент прироста показывает, на какую долю увеличился или уменьшился последующий уровень по сравнению с предыдущим, т.е.
где ΔК – коэффициент прироста уровня, выраженный в долях; ΔУi – абсолютный прирост уровня; Уi-1 – предыдущий уровень. Темп прироста, выраженный в процентах, показывает, на сколько процентов увеличился или уменьшился последующий уровень по сравнению с предыдущим, т.е.
Пример. Валовой сбор семян многолетних трав во всех категориях хозяйств административного района составил: в 2009 г. – 45 т, в 2010 г. – 48 т. Необходимо найти темп прироста сбора семян в 2010 г. по сравнению с 2009 г. Для решения прежде всего найдем абсолютный прирост уровней:
Темпы прироста также, как и темпы роста, могут быть рассчитаны базисным и цепным способами. Между темпами прироста и темпами роста существует непосредственная связь. Поэтому коэффициент (темп) прироста можно выразить через темп роста, т.е.
Это означает, что коэффициент прироста всегда на единицу меньше соответствующего коэффициента роста. Если же темп прироста выражен в процентах, то он на 100 процентных пунктов меньше темпов роста. Допустим, если темп роста урожайности зерновых культур составил 118 %, то темп прироста составит:
Отсюда следует, что при наличии темпа роста можно удобно и быстро определить темп прироста. Темпы прироста могут быть выражены положительными (+) и отрицательными (-) значениями. При этом положительные значения темпа указывают на рост последующего уровня по сравнению с предыдущим; отрицательное же значение указывает на его снижение. В последнем случае говорят о темпе снижения. Результаты исчисления базисных и цепных темпов прироста и снижения покажем на примере динамики реализованных фруктов специализированной сельскохозяйственной организацией (табл. 9.5).
Т а б л и ц а 9.5. Динамика реализации фруктов
Как видно, темпы роста и темпы прироста в динамике снижаются. Это свидетельствует об убывающем характере динамики реализованной продукции. Темпы прироста за весь изучаемый период в динамическом ряду могут быть охарактеризованы при помощи их среднего значения. При расчете среднего темпа прироста можно исходить из значения среднего темпа роста, т.е.
где Допустим, необходимо определить среднегодовой темп прироста валового сбора картофеля в фермерском хозяйстве за период 2008 – 2010 гг., если в 2008 г. было произведено 120 т, в 2010 – 150 т картофеля. Прежде всего рассчитаем средний темп валового сбора картофеля по формуле (9.11), т.е.,
Затем находим средний темп прироста производства картофеля:
Значит, ежегодный прирост валового сбора картофеля в фермерском хозяйстве за период 2008 – 2010 гг. составил в среднем 11, 8%.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.194.225 (0.014 с.) |

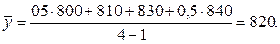
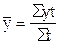 , (9.1)
, (9.1)
 (9.2)
(9.2)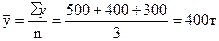 .
. , (9.3)
, (9.3) .
. тыс. тонн, т.е. объем госзакупок в 2010 г. возрос по сравнению с 2009 г. на 5 тыс. тонн.
тыс. тонн, т.е. объем госзакупок в 2010 г. возрос по сравнению с 2009 г. на 5 тыс. тонн. тыс. тонн.
тыс. тонн.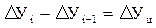 . (9.5)
. (9.5) (9.6)
(9.6)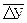 – средний абсолютный прирост; n – число цепных абсолютных приростов.
– средний абсолютный прирост; n – число цепных абсолютных приростов.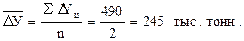
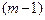 . Следовательно, средний абсолютный прирост можно выразить в виде:
. Следовательно, средний абсолютный прирост можно выразить в виде: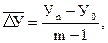 (10.7)
(10.7)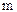 – число уровней ряда.
– число уровней ряда.
 (9.8)
(9.8)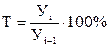 (9.9)
(9.9)
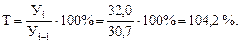
 (9.10)
(9.10)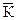 –– средний коэффициент роста за весь период; К1, К2, К3….Кn –– цепные коэффициенты роста за каждый отдельный промежуток времени; n –– число темпов роста.
–– средний коэффициент роста за весь период; К1, К2, К3….Кn –– цепные коэффициенты роста за каждый отдельный промежуток времени; n –– число темпов роста.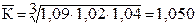 раза (105,0 %).
раза (105,0 %).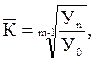 (9.11)
(9.11)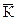 –– средний темп роста; Уп –– конечный уровень ряда; У0 –– начальный уровень; m –– число уровней в динамическом ряду.
–– средний темп роста; Уп –– конечный уровень ряда; У0 –– начальный уровень; m –– число уровней в динамическом ряду. (129,2 %).
(129,2 %).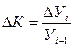 , (9.12)
, (9.12) . (9.13)
. (9.13)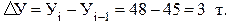 .Затем рассчитаем темп прироста:
.Затем рассчитаем темп прироста: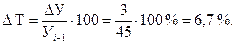
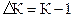 , или
, или  . (9.14)
. (9.14)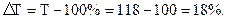
 (9.15)
(9.15)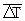 –– средний темп прироста;
–– средний темп прироста;  –– средний темп роста.
–– средний темп роста.