
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент множественной корреляцииСодержание книги
Поиск на нашем сайте
При изучении тесноты связи между несколькими факторными и результативными признаками рассчитывают совокупный коэффициент множественной корреляции. Так, при определении совокупной меры тесноты связи между признаком-результатом и двумя факторными признаками теоретически обоснованной является формула
где R xyz – совокупный коэффициент корреляции между признаками-факторами (x, z) и результативным признаком (у); r xу – парный коэффициент корреляции между первым фактором (х) и результатом (у); r zy – парный коэффициент корреляции между вторым фактором (z) и результатом (у); r xz – парный коэффициент корреляции между факторными признаками (x, z). Из формулы (11.5) видно, что для расчета коэффициента множественной корреляции необходимо прежде всего найти соответствующие парные коэффициенты, характеризующие тесноту связи между изучаемыми признаками. Коэффициент множественной корреляции является всегда положительным числом и принимает любые значения в пределах между 0 и 1. Чем ближе он к единице, тем теснее зависимость результативного признака от совокупного действия изучаемых факторов. При этом сочетание противодействующих (прямых и обратных) признаков-факторов проявляется через их накопительное влияние, что и повышает коэффициент множественной корреляции. Допустим, необходимо рассчитать коэффициент корреляции, характеризующий влияние урожайности зерновых культур и годового удоя коров на производительность труда в сельскохозяйственных организациях. С этой целью собрана необходимая информация по 100 хозяйствам. Прежде всего рассчитаны парные коэффициенты корреляции: между первым фактором – урожайностью зерновых культур (х) и производительностью труда (у) –– r xy =0,55; вторым фактором – годовым удоем коров (z) и производительностью труда (у) –– z xy =0,67; урожайностью зерновых культур и годовым удоем коров –– r xz =0,72. Подставим эти данные в формулу (11.5) и получим:
Таким образом, совместное воздействие урожайности зерновых культур и годового удоя коров на производительность труда в сельскохозяйственных организациях, выявленное посредством коэффициента множественной корреляции (Rxyz=0,68), можно оценить как близкое к тесному. Показатели детерминации
При изучении количественного влияния признаков-факторов на результаты важно определить, какая часть результативного признака непосредственно обусловлена воздействием вариации изучаемых факторных признаков. С этой целью могут быть рассчитаны различные показатели детерминации. Наиболее универсальный показатель детерминации – доля систематических (факторных) вариаций в структуре общей вариации результативного признака. Например, при изучении влияния качества продукции на ее реализационные цены доля факторной вариации составила 0,8 (80 %). Это означает, что прямое влияние качества на формирование цен реализации продукции можно гарантировать не менее, чем на 80 %. Доля же случайной (остаточной) вариации (20 %) показывает, в какой мере колебания реализационных цен обусловлены влиянием прочих (неучтенных) факторов. В тех случаях, когда для измерения тесноты связи между признаками приходится рассчитывать коэффициенты парной или множественной корреляции, для оценки количественной меры непосредственного влияния факторных признаков на результаты необходимо определить так называемый коэффициент детерминации, который нередко выражают в процентах:
где r – коэффициент корреляции (парной или множественной). Коэффициент детерминации, называемый в некоторых случаях показателем «координации», характеризует долю фактической дисперсии результативного признака, объясняемую вариацией изучаемых факторов. Например, если коэффициент парной корреляции между дозами органических удобрений и урожайностью картофеля в крестьянских хозяйствах составляет 0,65, то прямое влияние вариации доз удобрений на вариацию урожайности можно оценить не менее, чем на 42,3 % (0,652 · 100). Дополнение до 100 % (или до единицы) показывает, в какой количественной мере колебания признака-результата обусловлены вариацией прочих (неучтенных) факторов. Следовательно, совокупное влияние вариации остальных факторов (кроме доз органики) на вариацию урожайности картофеля в крестьянских хозяйствах может составить не более 57,7 % (100 – 42,3).
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.54.210 (0.006 с.) |

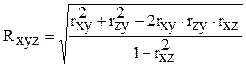 , (11.5)
, (11.5)
 , (11.6)
, (11.6)


