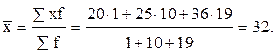Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взвешенной урожайности зерновых и зернобобовых культурСодержание книги
Поиск на нашем сайте
Для расчёта средней урожайности зерновых и зернобобовых культур с учётом применения второго и третьего свойств средней воспользуемся данными табл. 6.3., получим:
Таким образом, применение второго и третьего свойств позволило упростить технику расчёта средней урожайности. Использование четвёртого свойства проверим также на примере данных табл. 6.4:
как видим, полученный результат (6,4 тыс. т) соответствует валовому сбору, показанному в табл. 6.4, что и подтверждает справедливость четвёртого свойства средней арифметической величины. Она обладает многими другими свойствами, но они играют менее важную роль и поэтому нами не рассматриваются.
Средняя хронологическая величина Одна из разновидностей средней арифметической величины – средняя хронологическая. Исчисленную по совокупности значений признака в разные моменты или за различные периоды времени, принято называть средней хронологической, применяемой для нахождения среднего уровня в динамических рядах. В отличие от вариационного ряда, характеризующего изменение явлений в пространстве, динамический ряд представляет собой такой ряд чисел, который характеризует изменение явлений во времени. Иногда их называют временными или хронологическими. В зависимости от вида динамических рядов для определения их средних уровней могут быть применены соответствующие приемы расчёта средней хронологической величины. Так, при нарождении среднего уровня в периодическом ряду динамики возможно применение средней арифметической простой или взвешенной. Если же необходимо рассчитать средний уровень моментного ряда динамики с равными промежутками времени между моментами, то целесообразно воспользоваться приемом средней хронологической моментного ряда с равными интервалами:
где Например, в сельскохозяйственной организации (СХО) по состоянию на начало каждого месяца 2010 г. имелось следующее поголовье свиней: на 1 января – 500; на 1 февраля – 600; на 1 марта – 800; на 1 апреля – 1000 голов. По этим данным необходимо рассчитать среднеквартальную численность свиней в СХО. Условно считается, что промежутки (интервалы) времени между начальными моментами (датами) каждого предыдущего и последующего месяца равны между собой. Следовательно, для расчёта среднеквартального поголовья свиней можно применить формулу (6.5). Подставим соответствующие данные и получим:
Это означает, что в среднем ежемесячно за первый квартал 2010 г. в СХО имелось 717 голов свиней. В тех случаях, когда необходимо определить средний уровень моментного ряда динамики с неравными промежутками между моментами, обычно используют формулу средней арифметической взвешенной величины (6.4). Например, численность работников в бригаде СХО составляла: на 1 апреля – 20 человек, на 11 апреля –25, на 30 апреля – 36 человек. Необходимо рассчитать среднемесячную численность работников в бригаде за апрель. Как видно из приведённых данных, промежутки времени между указанными моментами (датами) не равны между собой: можно предположить, что в бригаде было на протяжении 1 дня – 20 человек, 10 дней – 25, 19 дней – 36. Следовательно, для расчета среднемесячной численности работников в бригаде воспользуемся формулой (6.4) и получим:
Таким образом, за апрель в бригаде СХО числилось в среднем 32 работника. В системе агропромышленного комплекса средняя хронологическая величина может применяться при расчёте средней годовой, квартальной, месячной численности работников, поголовья различных видов и групп сельскохозяйственных животных, наличия различных видов машинно-тракторного парка и других случаях.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

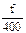
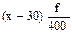

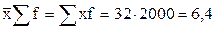 тыс.т
тыс.т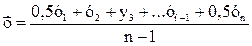 , (6.5)
, (6.5)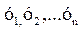 – порядковые уровни моментного ряда; n – число моментов в ряду.
– порядковые уровни моментного ряда; n – число моментов в ряду.