
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средняя гармоническая величинаСодержание книги
Поиск на нашем сайте
При условии подстановки в общую формулу (6.1) значения к= –1 можно получить среднюю гармоническую величину, которая имеет простую и взвешенную формы. Для ранжированного ряда используется средняя гармоническая простая величина, которую можно записать следующим образом.
где n – общая численность вариант; Допустим, имеются данные о том, что при перевозке картофеля скорость движения автомобиля с грузом составляет 30 км/ч, без груза – 60 км/ч. Необходимо найти среднюю скорость движения автомобиля. На первый взгляд представляется совсем несложное решение задачи: применить способ средней арифметической простой величины, т.е. Однако, если иметь в виду, что скорость движения равна пройденному пути, разделённому на затраченное время, то совершенно очевидно, что результат (45 км/ч) оказывается неточным, так как на прохождение одного и того же пути автомобилем с грузом и без груза (туда и обратно) затраты времени будут существенно различаться. Следовательно, более точная средняя скорость движения автомобиля с грузом и без груза может быть рассчитана по средней гармонической простой величине:
Таким образом, средняя скорость движения автомобиля с грузом и без груза составляет не 45, а 40 км/ч. В дискретных или интервальных рядах используется средняя гармоническая взвешенная величина:
где W – произведение варианты на частоту (взвешенная варианта, xf). Рассмотрим пример. Трудоемкость производства 1т картофеля в первом подразделении сельскохозяйственной организации составляет 10 чел.-ч., во втором – 30 чел.-ч. В обоих подразделениях на производство картофеля затрачено по 30 тыс. чел.-ч. Необходимо рассчитать среднюю арифметическую трудоёмкость картофеля в сельскохозяйственной организации. Кажется, что среднюю трудоёмкость легко найти как полусумму трудоёмкости картофеля в двух подразделениях, т. е. по способу средней арифметической простой величины:
Однако, при таком решении совершаются две ошибки. Первая, принципиальная ошибка заключается в том, что при расчёте средней трудоемкости по способу средней арифметической простой величины не учитывается сущность самой трудоемкости, которая находится как отношение прямых затрат труда к объему продукции. Вторая ошибка состоит в том, что при решении не учтен приведенный по условию задачи конкретный объем затрат труда на производство картофеля (по 30 тыс. чел.-ч. в обоих подразделениях). Это позволяет рассчитать частоту (веса) для трудоемкости картофеля и, таким образом, найти среднюю арифметическую взвешенную трудоемкость, что будет успешно заменено путем применения средней гармонической взвешенной величины:
Таким образом, средняя трудоёмкость картофеля в сельхозорганизации составляет не 20, как это было рассчитано выше, а 15 чел. ч/т. Средняя гармоническая величина применяется главным образом в тех случаях, когда варианты ряда представлены обратными значениями, а частоты (веса) скрыты в общем объеме изучаемого признака.
Структурные средние В некоторых случаях для получения обобщающей характеристики статистической совокупности по какому-либо признаку приходится пользоваться так называемыми структурным средними. К ним относят моду и медиану. Мода представляет собой варианту, наиболее часто встречающуюся в данной статистической совокупности. В ранжированном ряду мода как правило, не определяется, так как каждой варианте соответствует частота, равная единице. Мода в дискретном ряду соответствует варианте с наибольшей частотой, при этом случайная величина может иметь несколько мод. При наличии одной из них распределение статистической совокупности принято называть одномодальным, при наличии двух мод – бимодальным, трех и более мод – мультимодальным. Наличие нескольких мод нередко означает объединение в одной совокупности разнокачественных статистических единиц. Мода для интервального ряда с равными интервалами рассчитывается по формуле
где хмо – нижняя граница модального интервала; iмо – величина интервала; fмо – частота модального интервала; fдмо – частота домодального интервала; fзмо – частота замодального интервала. Допустим, рыночные цены на яблоки по районным центрам области сложились следующим образом (табл. 6.8). По этим данным необходимо рассчитать моду рыночных цен на картофель.
Т а б л и ц а 6.8. Рыночные цены на яблоки
Из данных табл. 6.8 видно, что максимальное число рынков сосредоточено в третьем интервале, причем распределение статистической совокупности унимодальное. Для расчёта моды рыночных цен на яблоки воспользуемся формулой (6.12):
Таким образом, модальная рыночная цена на яблоки в районных центрах области составляет 1690 р/кг. Модальная варианта при характеристике статистической совокупности может быть использована в тех случаях, когда расчёт средней величины затруднен либо невозможен, например, в рыночных условиях при изучении спроса и предложения, уровня цен и т.д. Медиана – варианта, находящиеся в середине вариационного ряда. Медиана в ранжированном ряду находится следующим образом. Во-первых, рассчитывают номер медианой варианты:
где nме – номер медианой варианты; n – общее число вариант в ряду. Во-вторых, в ранжированном ряду определяется значение медианой варианты: если общее число вариант нечетное, то медиана соответствует рассчитанному по формуле (6.13) номеру. Допустим, ранжированный ряд состоит из 99 единиц, распределенных по урожайности сахарной свеклы. Медианный номер варианты находим по формуле (6.13): Это означает, что под № 50 находится искомая медиана урожайности, которая равна, например, 500ц/га. Если же общее число вариант четное, то медиана равна полумсуме двух смежных медианных вариант. Например, в ранжированном ряду имеется 100 статистических единиц, распределенных опять-таки по урожайности сахарной свеклы. Следовательно, в таком ряду имеется два медианных номера, что видно из следующего расчета по формуле (6.13):
Значит, в этом случае медианными считаются № 50 и 51, а медиану урожайности сахарной свеклы, например, можно рассчитать как следующую полусумму двух смежных урожайностей, т.е.
Для дискретного ряда распределения медиану рассчитывают по накопленным частотам: во-первых, находят полусумму накопленных частот; во-вторых, определяют соответствие этой полусуммы конкретной варианте, которая и будет медианой. Например, годовой удой коров распределен в виде дискретного ряда, в котором сумма накопленных частот составляет 200 единиц и, соответственно, полусумма – 100 единиц. Этот медианный номер находится в группе статистических единиц дискретного ряда и соответствует годовому удою коров 5000 кг молока, что и является медианой дискретного ряда. В интервальном вариационном ряду медиану рассчитывают по формуле
где Ме – медиана интервального ряда; хме – нижняя граница медианного интервала; iме – величина медианного интервала; Σf – сумма накопленных частот в интервальном ряду; fн – накопленная частота домедианного интервала; fме – частота медианного интервала. Для расчёта медианы в интервальном ряду воспользуемся следующими данными (табл.6.9).
Т а б л и ц а 6.9. Урожайность картофеля в личных подсобных Хозяйствах населения
Из данных табл. 6.9 прежде всего видно, что медианным является четвертый интервал. Кроме того, несложный подсчёт показывает, что сумма накопленных частот (общее число хозяйств) составляет 200 единиц, а накопленная частота домедианного интервала – 90 единиц. Воспользуемся формулой (6.14) и рассчитаем медианную урожайность картофеля:
Таким образом, медианная урожайность картофеля в личных подсобных хозяйствах населения составляет 256 ц/га. Применение медианы имеет специфический характер. Так, если вариационный ряд относительно небольшой, то на величину средней арифметической могут оказать влияние случайные колебания крайних вариант, что никак не скажется на размере медианы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.35.129 (0.006 с.) |

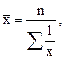 (6.10)
(6.10) – обратное значение варианты.
– обратное значение варианты.

 (6.11)
(6.11)

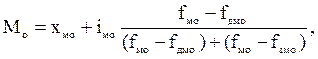 (6.12)
(6.12)
 , (6.13)
, (6.13) .
.

 , (6.14)
, (6.14)



