Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Степенные средние величины в статистике: средняя арифметическая, средняя квадратическая, средняя гармоническая. Взвешенные и простые средние степенные величины.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Средние величины открыли ученые Петте и Кетле. Они определили, что постоянные величины действуют одинаково на каждое изучаемое явление. Эти величины похожи друг на друга и создают общие для всех закономерности. Следствием их изучения явилось выделение средних величин в качестве основного приема статичтического анализа. Математическая статистика выводит средние из формул степенной средней:
- среднее значение исследуемого явления. x - значение признака (варианта). n - число признаков. m - показатель степени средней. В зависимости от значения показателя степени m различают следуещие виды степенных средних: При m = - 1 - среднее гармоническое (xгар ) При m = 0 - среднее геометрическое (xг ) При m = 1 - среднее арифметическое (xар ) При m = 2 - среднее квадратическое(xкв ) При m = 3 - среднее кубическое (xкуб ) Виды средних величин 1.
средняя арифметическая простая применяется, когда перечислены все значения усредненного признака:
x - значение признака n - кол-во единиц обладающих данным признаком. 2. среднее арифметическое взвешенное применяется, когда задан «вес признака»(кол-во единиц, обладающих одинаковым признаком)
3. средняя гармоническая простая.
4. средняя гармоническая взвешенная применяется, когда задан объем признака – это суммарное значение признака по всей совокупности или по группам.
x - значение признака. w - объем признака. 5. средняя геометрическая простая.
x - значение признака. k - кол-во осредняемых величин. 6. средняя геометрическая взвешенная.
7. среднее хронологическое применяется в рядах динамики
x n - конечный уровень ряда n - число уровней в ряду 8. средняя квадратическая простая 9.
средняя квадратическая взвешенная
10. средняя кубическая простая
11. средняя кубическая взвешенная
Вариация признака. Абсолютные показатели вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение. Относительные показатели вариации: коэффициенты осцилляции и вариации. Показатели варьирования осредненных статичтических признаков: размах вариации, среднее линейное отклонение, среднее кватратическое отклонение (дисперсия), коэффициент вариации. Расчетные формулы и порядок расчета показателей вариации. Применение показателей вариации при анализе статистических данных в деятельности предприятий и организаций, учреждений БР, макроэкономических показателей. Средний показатель дает обобщающий, типичный уровень признака, но не показывает степень его колеблемости, вариации. Поэтому средние показатели необходимо дополнять показателями вариации. От размера и распределения от клонений зависит надежность средних показателей. Важно знать основные показатели вариации, уметь правильно их рассчитывать и использовать. Основными показателями вариации являются: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Формулы показателей вариации: 1. размах вариации.
Xμαχ - максимальное значение признака Xmin - минимальное значение признака. Размах вариации может служить лишь приближенной мерой вариации признака, т.к. он исчисляется на основе двух крайних ее значений, а остальные во внимание не принимаются; при этом крайние значения признака для данной совокупности могут быть чисто случайными. 2. среднее линейное отклонение.
[X-X] - означает, что отклонения берутся без учета их знака. Среднее линейное отклонение довольно редко используется в экономическом статистическом анализе. 3. Дисперсия.
4. Среднее квадратическое отклонение.
Относительные показатели вариации: коэффициенты осцилляции, вариации. Коэффициент вариации. Коэффициент вариации дает относительную оценку вариации и позволяет сравнить степень вариации признаков в рядах с разным уровнем средних. Если коэффициент вариации V>33%, то она не надежна, ей доверять нельзя, совокупность неоднородна. Если V<33%, то средняя надежна. Коэффициент осциляции.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 786; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.202.168 (0.008 с.) |




 x - значение признака, f - вес признака
x - значение признака, f - вес признака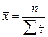
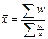


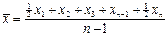 x1 - начальный уровень ряда
x1 - начальный уровень ряда