
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средняя длина свободного пробега молекул.Содержание книги
Поиск на нашем сайте Под средней длиной свободного пробега понимают среднее расстояние, которое проходит молекула между двумя последовательными соударениями. За секунду молекула в среднем проходит расстояние, численно равное ее средней скорости
Молекула столкнется со всеми неподвижными молекулами, центры которых находятся в пределах ломаного цилиндра диаметром 2d. За секунду молекула проходит путь, равный
В действительности движутся все молекулы. Поэтому число столкновений за одну секунду будет несколько большим полученной величины, так как вследствие движения окружающих молекул рассматриваемая молекула испытала бы некоторое число соударений даже в том случае, если бы она сама оставалась неподвижной. Предположение о неподвижности всех молекул, с которыми сталкивается рассматриваемая молекула, будет снято, если в формулу (3.1.2) вместо средней скорости
Предположим, что скорости молекул до столкновения были
Так как углы
от произведения этих величин равно произведению их средних. Поэтому
С учетом последнего равенства формулу (3.1.4) можно переписать в виде:
так как
т. е.
Поэтому соотношение (3.1.6) можно представить так:
С учетом последнего выражения формула для средней длины свободного пробега приобретает вид:
Для идеального газа
Отсюда видно, что при изотермическом расширении (сжатии) средняя длина свободного пробега растет (убывает). Как было отмечено во введении, эффективный диаметр молекул убывает с ростом температуры. Поэтому при заданной концентрации молекул средняя длина свободного пробега увеличивается с ростом температуры. Вычисление средней длины свободного пробега для азота (d = 3•10-10 м), находящегося при нормальных условиях (р = 1,01•105 Па, Т = 273,15 К) дает:
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 585; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

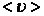 Если за это же время она испытает в среднем
Если за это же время она испытает в среднем 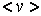 столкновений с другими молекулами, то ее средняя длина свободного пробега
столкновений с другими молекулами, то ее средняя длина свободного пробега 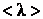 , очевидно, будет равна
, очевидно, будет равна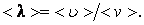 (3.1.1)
(3.1.1)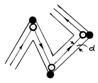
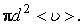 Если в единице объема газа находится n молекул, то число столкновений рассматриваемой молекулы за одну секунду будет равно
Если в единице объема газа находится n молекул, то число столкновений рассматриваемой молекулы за одну секунду будет равно 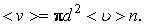 (3.1.2)
(3.1.2) рассматриваемой молекулы. В самом деле, если налетающая молекула движется со средней относительной скоростью
рассматриваемой молекулы. В самом деле, если налетающая молекула движется со средней относительной скоростью 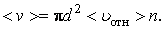 (3.1.3)
(3.1.3)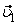 и
и 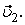 Тогда
Тогда 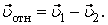 Из треугольника скоростей имеем (рис. 2)
Из треугольника скоростей имеем (рис. 2)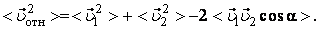
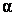 и скорости
и скорости 
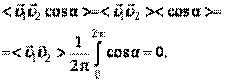 (3.1.5)
(3.1.5)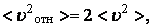 (3.1.6)
(3.1.6)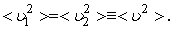 Cредняя квадратичная скорость пропорциональна средней скорости,
Cредняя квадратичная скорость пропорциональна средней скорости, (3.1.7)
(3.1.7)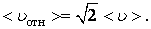
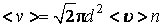 (3.1.8)
(3.1.8)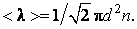 (3.1.9)
(3.1.9)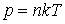 Поэтому
Поэтому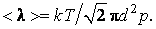 (3.1.10)
(3.1.10)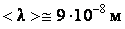 , а для числа столкновений за одну секунду:
, а для числа столкновений за одну секунду: 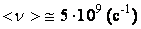 . Таким образом, средняя длина свободного пробега молекул при нормальных условиях составляет доли микрон, а число столкновений – несколько миллиардов в секунду. Поэтому процессы выравнивания температур (теплопроводность), скоростей движения слоев газа (вязкое трение) и концентраций (диффузия) являются достаточно медленными, что подтверждается опытом.
. Таким образом, средняя длина свободного пробега молекул при нормальных условиях составляет доли микрон, а число столкновений – несколько миллиардов в секунду. Поэтому процессы выравнивания температур (теплопроводность), скоростей движения слоев газа (вязкое трение) и концентраций (диффузия) являются достаточно медленными, что подтверждается опытом.


