Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внутреннее трение(вязкость) как явление переноса.Содержание книги
Поиск на нашем сайте (См в1) Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.
Вязкость - сопротивление, оказываемое телом движению отдельной его части без нарушения связи целого. Такое движение составляет характеристику жидкостей, как "капельных", так и "упругих", т. е. газов.
5.Течение вязкой жидкости по трубам. Метод Пуазейля определения коэффициента вязкости.
Тече́ние Пуазёйля — ламинарное течение жидкости через каналы в виде прямого кругового цилиндра или слоя между параллельными плоскостями. Течение Пуазёйля — одно из самых простых точных решений уравнений Навье — Стокса. Описывается законом Пуазёйля (Хагена — Пуазёйля). Закон Пуазёйля (иногда закон Хагена — Пуазёйля) — это физический закон так называемого течения Пуазёйля, то есть установившегося течения вязкой несжимаемой жидкости в тонкой цилиндрической трубке. Закон установлен эмпирически в1839 году Г. Хагеном, а в 1840—1841 годы — независимо Ж. Л. Пуазёйлем. Теоретически объяснён Дж. Г. Стоксом в 1845 году. При установившемся ламинарном движении вязкой несжимаемой жидкости сквозь цилиндрическую трубу круглого сечения секундный объёмный расход прямо пропорционален перепаду давления на единицу длины трубы и четвертой степени радиуса и обратно пропорционален коэффициенту вязкости жидкости.
где · · Q — секундный объёмный расход жидкости, м³/с; · R — радиус капилляра, м; · d — диаметр капилляра, м; · · l — длина трубы, м. Формула используется для определения вязкости жидкостей. Другим способом определения вязкости жидкости является метод, использующий закон Стокса.
Пологая течение жидкости ламинарным, найдём закон изменения скорости v с расстоянием r от оси трубы, т.е. v(r) -? Выделим воображаемый цилиндрический объём жидкости радиуса r и длинны l. Поскольку скорости всех частиц жидкости являются постоянными v = const, сумма внешних сил, приложенных к любому объёму жидкости, равна нулю. На основание цилиндра действуют силы давления, сумма которых равна:
На боковую поверхность цилиндра действует сила трения:
Поскольку
Учитывая, что скорость убывает с расстоянием от оси трубы, т.е. из (1) получим: Интегрирование даёт:
Если
Вычислим поток жидкости Q – т. е. объём жидкости, протекающей через поперечное сечение трубы за единицу времени. Для этого сначала определим поток жидкости через кольцо радиуса r и толщиной dr:
Интегрируя по r, получим поток жидкости через поперечное сечение трубы:
Ее можно использовать для определения коэффициента вязкости
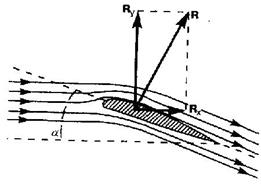
6.Движение тел в жидкости и газе. Метод Стокса определения коэффициента вязкости. Одной из важнейших задач гидро- и аэродинамики является изучение движения твердых тел в газе и жидкости, в частности изучение тех сил, с которыми среда воздействует на движущееся тело. Эта задача стала особенно значимой в связи с бурным развитием авиации и значительным увеличением скорости движения морских судов. На тело, которое движется в жидкости или газе, действуют две силы (равнодействующую их обозначим R), одна из которых (Rx) направлена в сторону, противоположную движению тела (в сторону потока), - лобовое сопротивление, а вторая (Ry) перпендикулярна этому направлению - подъемная сила (рис. 1).
Рис.1
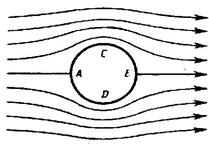
Рис.2
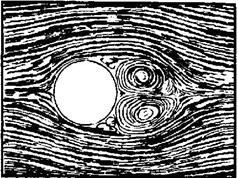
Другим образом обстоит дело если происходит движение тела в вязкой жидкости (особенно при увеличении скорости обтекания). Из-за вязкости среды в области движения, прилегающей к поверхности тела, создается пограничный слой частиц, которые движутся с меньшими скоростями. В результате тормозящего действия этого слоя частицы начинают вращаться и движение жидкости в пограничном слое становится вихревым. Если тело не обладает обтекаемой формой (нет плавно утончающейся хвостовой части), то происходит отрыв пограничного слоя жидкости от поверхности тела. При этом за телом возникает течение жидкости (газа), которое направлено противоположно набегающему потоку. Оторвавшийся пограничный слой, следуя за этим течением, образует вихри, вращающиеся в противоположные стороны (рис. 3).
Рис.3
Лобовое сопротивление зависит от формы тела и его положения относительно потока, что учитывается безразмерным коэффициентом сопротивления Cx, который определяется экспериментально:
Составляющую Rx можно значительно уменьшить, если подобрать тело формы, не способствующей образованию завихрения. Подъемная сила может быть определена формулой, аналогичной (1):
Для крыла самолета требуется значительная подъемная сила при малом лобовом сопротивлении (это условие выполняется при малыхуглах атаки α (угол к потоку); см. рис. 1). Крыло тем лучше удовлетворяет этому условию, чем больше величина К=Cy/Cx называемаякачеством крыла. Большие заслуги в конструировании требуемого профиля крыла и изучении влияния геометрической формы тела на коэффициент подъемной силы принадлежат Н. Е. Жуковскому (1847-1921).
В этом методе шарик падает в исследуемой жидкости. В установившимся режиме падения шарик будет двигаться с постоянной скоростью. Следовательно, ускорение шарика будет равно нулю и, согласно второму закону Ньютона, сумма действующих на него сил будет равна нулю. На шарик действуют. Сила Архимеда (см. рис. 1.35)
Рис. 1.35. Метод Стокса FA=mж·g=(4/3)·π·r3·ρж·g, где ρж - плотность жидкости, r - радиус шарика. Сила тяжести m·g=(4/3)·π·r3·ρ·g, где ρ - плотность материала шарика. Сила вязкого трения, которая для тел сферической формы определяется формулой Стокса Fтр=6π·η·r·v, где v - скорость шарика в установившемся режиме, η - искомый коэффициент вязкости. На основании второго закона Ньютона запишем: (4/3)·π·r3·ρ·g=(4/3)·π·r3·ρж·g + 6π·η·r·v Отсюда получим искомое выражение для коэффициента вязкости: (4/3)·π·r3·g·(ρ-ρж)=6π·η·r·v → η=[(4/3)·π·r3·g·(ρ-ρж)] / 6π··r·v
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 2362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

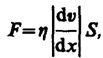 (48.5)
(48.5)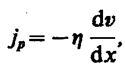 (48.6)
(48.6)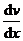 — градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки jр и
— градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости (поэтому знаки jр и 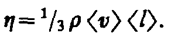 (48.7)
(48.7)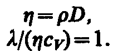
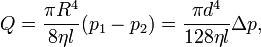
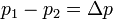 — перепад давления на концах капилляра, Па;
— перепад давления на концах капилляра, Па;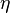 — коэффициент динамической вязкости, Па·с;
— коэффициент динамической вязкости, Па·с;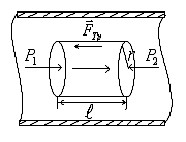
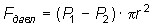 .
.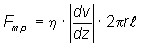 .
.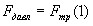 , то
, то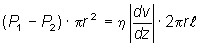 .
.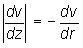 ,
,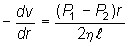 ,
, 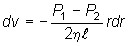 .
.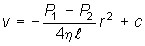 . Так как при r = R скорость v = 0, то
. Так как при r = R скорость v = 0, то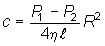 , где R – радиус трубы.
, где R – радиус трубы.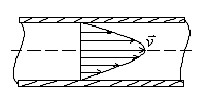
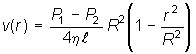 - закон изменения скорости жидкости от расстояния до оси трубы.
- закон изменения скорости жидкости от расстояния до оси трубы.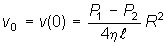 - скорость на оси трубы, то
- скорость на оси трубы, то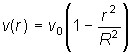
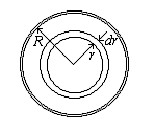

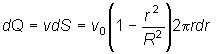 -поток жидкости через кольцо dr.
-поток жидкости через кольцо dr.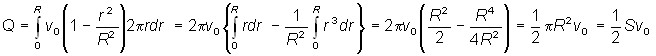
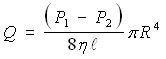 -формула Пуазейля.
-формула Пуазейля.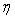
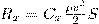 (1) где ρ - плотность среды; ν - скорость движения тела; S - наибольшее поперечное сечение тела.
(1) где ρ - плотность среды; ν - скорость движения тела; S - наибольшее поперечное сечение тела.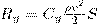 где Cy - безразмерный коэффициент подъемной силы.
где Cy - безразмерный коэффициент подъемной силы.