Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы и потенциальная энергия взаимодействия молекул . Строение газов, жидкостей и твердых тел. Явление теплового расширения твердых тел.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
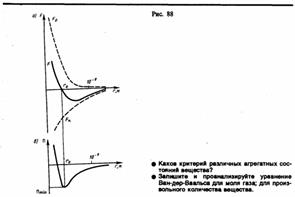
Модель идеального газа, используемая в молекулярно-кинетической теории газов, позволяет описывать поведение разреженных реальных газов при достаточно высоких температурах и низких давлениях. При выводе уравнения состояния идеального газа размерами молекул и их взаимодействием друг с другом пренебрегают. Повышение давления приводит к уменьшению среднего расстояния между молекулами, поэтому необходимо учитывать объем молекул и взаимодействие между ними. Taк, в 1 м3 газа при нормальных условиях содержится 2,68×1025 молекул, занимающих объем примерно 10–4 м3 (радиус молекулы примерно 10–10 м), которым по сравнению с объемом газа (1 м3) можно пренебречь. При давлении 500 МПа (1 атм = 101,3 кПа) объем молекул составит уже половину всего объема газа. Таким образом, при высоких давлениях и низких температурах указанная модель идеального газа непригодна. При рассмотрении реальных газов — газов, свойства которых зависят от взаимодействия молекул, надо учитывать силы межмолекулярного взаимодействия. Они проявляются на расстояниях £ 10–9 м и быстро убывают при увеличении расстояния между молекулами. Такие силы называются короткодействующими. По мере развития представлений о строении атома и квантовой механики, было выяснено, что между молекулами вещества одновременно действуют силы притяжения и силы отталкивания. На рис. 88, а приведена качественная зависимость сил межмолекулярного взаимодействия от расстояния r между молекулами, где F о и F п — соответственно силы отталкивания и притяжения, a F — их результирующая. Силы отталкивания считаются положительными, а силы взаимного притяжения — отрицательными.
На расстоянии r=r 0 результирующая сила F = 0, т.е. силы притяжения и отталкивания уравновешивают друг друга. Таким образом, расстояние r 0 соответствует равновесному расстоянию между молекулами, на котором бы они находились в отсутствие теплового движения. При r < r 0 преобладают силы отталкивания (F> 0), при r > r 0 — силы притяжения (F <0). На расстояниях r > 10–9 м межмолекулярные силы взаимодействия практически отсутствуют (F ®0). Элементарная работа dA силы F при увеличении расстояния между молекулами на d r совершается за счет уменьшения взаимной потенциальной энергии молекул, т. е.
Из анализа качественной зависимости потенциальной энергии взаимодействия молекул от расстояния между ними (рис. 88, б) следует, что если молекулы находятся друг от друга на расстоянии, на котором межмолекулярные силы взаимодействия не действуют (r ®¥), то П=0. При постепенном сближении молекул между, ними появляются силы притяжения (F <0), которые совершают положительную работу (dA=F d r > 0).Тогда, согласно (60.1), потенциальная энергия взаимодействия уменьшается, достигая минимума при r = r 0. При r < r 0 с уменьшением r силы отталкивания (F >0) резко возрастают и совершаемая против них работа отрицательна (dA=F d r <0). Потенциальная энергия начинает тоже резко возрастать и становится положительной. Из данной потенциальной кривой следует, что система из двух взаимодействующих молекул в состоянии устойчивого равновесия (r = r 0) обладает минимальной потенциальной энергией. Критерием различных агрегатных состояний вещества является соотношениемежду величинами Пmin и kT. Пmin — наименьшая потенциальная энергия взаимодействия молекул — определяет работу, которую нужно совершить против сил притяжения для того, чтобы разъединить молекулы, находящиеся в равновесии (r = r 0); kT определяет удвоенную среднюю энергию, приходящуюся на одну степень свободы хаотического (теплового) движения молекул. Если Пmin<< kT, то вещество находится в газообразном состоянии, так как интенсивное тепловое движение молекул препятствует соединению молекул, сблизившихся до расстояния r 0, т. е. вероятность образования агрегатов из молекул достаточно мала. Если Пmin>> kT, то вещество находится в твердом состоянии, так как молекулы, притягиваясь друг к другу, не могут удалиться на значительные расстояния и колеблются около положений равновесия, определяемого расстоянием r 0. Если Пmin» kT, то вещество находится в жидком состоянии, так как в результате теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояние, превышающее r 0. Таким образом, любое вещество в зависимости от температуры может находиться в газообразном, жидком или твердом агрегатном состоянии, причем температура перехода из одного агрегатного состояния в другое зависит от значения Пmin, для данного вещества. Например, у инертных газов Пmin мало, а у металлов велико, поэтому при обычных (комнатных) температурах они находятся соответственно в газообразном и твердом состояниях. Основные положения молекулярно-кинетической теории: · все вещества состоят из молекул, а молекулы из атомов, · атомы и молекулы находятся в постоянном движении, · между молекулами существуют силы притяжения и отталкивания.
В газах молекулы двигаются хаотически, расстояния между молекулами большие, молекулярные силы малы, газ занимает весь предоставленный ему объем. В жидкостях молекулы располагаются упорядочно только на малых расстояниях, а на больших расстояниях порядок (симметрия) расположения нарушается – “ближний порядок”. Силы молекулярного притяжения удерживают молекулы на близком расстоянии. Движение молекул – “перескоки ” из одного устойчивого положения в другое (как правило, в пределах одного слоя. Таким движением объясняется текучесть жидкости. Жидкость не имеет форму, но имеет объем. Твердые тела – вещества, которые сохраняют форму, делятся на кристаллические и аморфные. Кристаллические твердые тела имеют кристаллическую решетку, в узлах которой могут находиться ионы, молекулы или атомы Они совершают колебания относительно устойчивых положений равновесия.. Кристаллические решетки имеют правильную структуру по всему объему – “дальний порядок” расположения.
Аморфные тела сохраняют форму, но не имеют кристаллической решетки и, как следствие, не имеют ярко выраженной температуры плавления. Их называют застывшими жидкостями, так как они, как жидкости имеют “ближний ” порядок расположения молекул.
Подавляющее большинство веществ при нагревании расширяется. Это легко объяснимо с позиции механической теории теплоты, поскольку при нагревании молекулы или атомы вещества начинают двигаться быстрее. В твердых телах атомы начинают с большей амплитудой колебаться вокруг своего среднего положения в кристаллической решетке, и им требуется больше свободного пространства. В результате тело расширяется. Так же и жидкости и газы, по большей части, расширяются с повышением температуры по причине увеличения скорости теплового движения свободных молекул (см. Закон Бойля—Мариотта, Закон Шарля,Уравнение состояния идеального газа). Основной закон теплового расширения гласит, что тело с линейным размером L в соответствующем измерении при увеличении его температуры на Δ Т расширяется на величину Δ L, равную: Δ L = αL Δ T где α — так называемый коэффициент линейного теплового расширения. Аналогичные формулы имеются для расчета изменения площади и объема тела. В приведенном простейшем случае, когда коэффициент теплового расширения не зависит ни от температуры, ни от направления расширения, вещество будет равномерно расширяться по всем направлениям в строгом соответствии с вышеприведенной формулой. Для инженеров тепловое расширение — жизненно важное явление. Проектируя стальной мост через реку в городе с континентальным климатом, нельзя не учитывать возможного перепада температур в пределах от —40°C до +40°C в течение года. Такие перепады вызовут изменение общей длины моста вплоть до нескольких метров, и, чтобы мост не вздыбливался летом и не испытывал мощных нагрузок на разрыв зимой, проектировщики составляют мост из отдельных секций, соединяя их специальными термическими буферными сочленениями, которые представляют собой входящие в зацепление, но не соединенные жестко ряды зубьев, которые плотно смыкаются в жару и достаточно широко расходятся в стужу. На длинном мосту может насчитываться довольно много таких буферов. Однако не все материалы, особенно это касается кристаллических твердых тел, расширяются равномерно по всем направлениям. И далеко не все материалы расширяются одинаково при разных температурах. Самый яркий пример последнего рода — вода. При охлаждении вода сначала сжимается, как и большинство веществ. Однако, начиная с +4°C и до точки замерзания 0°C вода начинает расширяться при охлаждении и сжиматься при нагревании (с точки зрения приведенной выше формулы можно сказать, что в интервале температур от 0°C до +4°C коэффициент теплового расширения воды α принимает отрицательное значение). Именно благодаря этому редкому эффекту земные моря и океаны не промерзают до дна даже в самые сильные морозы: вода холоднее +4°C становится менее плотной, чем более теплая, и всплывает к поверхности, вытесняя ко дну воду с температурой выше +4°C. То, что лед имеет удельную плотность ниже плотности воды, — еще одно (хотя и не связанное с предыдущим) аномальное свойство воды, которому мы обязаны существованием жизни на нашей планете. Если бы не этот эффект, лед шел бы ко дну рек, озер и океанов, и они, опять же, вымерзли бы до дна, убив всё живое.
34.Законы идеального газа. Уравнение состояния идеального газа (менделеева-клапейрона). Законы Авогадро и Дальтона. В молекулярно-кинетической теории используется модель идеального газа, в которой считают: Реальные газы при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Рассмотрим эмпирические законы, описывающие поведение идеальных газов. 1. Закон Бойля – Мариотта: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная: pV=const при T=const, m=const (7) Процесс, протекающий при постоянной температуре, называется изотермическим. Кривая, изображающая зависимость между величинами p и V, характеризующими свойства вещества при постоянной температуре, называется изотермой. Изотермы представляют собой гиперболы, расположенные тем выше, чем выше температура, при которой происходит процесс (рис. 1).
2. Закон Гей-Люссака: объем данной массы газа при постоянном давлении изменяется с температурой линейно: V=V0(1+αt) при p=const, m=const (8) Здесь t - температура по шкале Цельсия, V0 - объем газа при 0 oС, α=(1/273) K-1 - температурный коэффициент объемного расширения газа. Процесс, протекающий при постоянном давлении и неизменной массе газа, называется изобарным. В ходе изобарного процесса для газа данной массы отношение объема к температуре постоянно: V/T=const. На диаграмме в координатах (V,t) этот процесс изображается прямой, называемой изобарой (рис. 2).
3. Закон Шарля: давление данной массы газа при постоянном объеме изменяется линейно с температурой: p=p0(1+αt) при p=const, m=const (9) Здесь t - температура по шкале Цельсия, p0 - давление газа при 0 oС, α=(1/273) K-1 - температурный коэффициент объемного расширения газа. Процесс, протекающий при постоянном объеме и неизменной массе газа, называется изохорным. В ходе изохорного процесса для газа данной массы отношение давления к температуре постоянно: P/T=const. На диаграмме в координатах этот процесс изображается прямой, называемой изохорой (рис. 3).
Вводя в формулах (8) и (9) термодинамическую температуру T, законам Гей-Люссака и Шарля можно придать более удобный вид: V=V0(1+αt)=V0[1+α(T-1/α)]=V0αT (10) Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. Так, при нормальных условиях один моль любого газа занимает объем 22,4 м-3. При одинаковых температуре и давлении любой газ содержит в единице объема одинаковое количество молекул. При нормальных условиях в 1 м3 любого газа содержится число частиц, называемое числом Лошмидта: NL=2,68·1025 м-3. Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений p1,p2,...,pnвходящих в нее газов: p=p1+p2+....+pn Парциальное давление – давление, которое создавал бы газ, входящий в состав газовой смеси, если бы он занимал объем, равный объему смеси при той же температуре.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1056; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

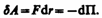 (60.1)
(60.1)