
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантовая оптика. Физика микромира. Молекулярная физика.Содержание книги
Поиск на нашем сайте
Квантовая оптика. Физика микромира. Молекулярная физика. 4.1. Тепловое излучение — электромагнитное излучение с непрерывным спектром, испускаемое нагретыми телами за счёт их тепловой энергии. Примером теплового излучения является свет от лампы накаливания. Мощность теплового излучения объекта, удовлетворяющего критериям абсолютно чёрного тела, описывается законом Стефана — Больцмана. Отношение излучательной и поглощательной способностей тел описывается законом излучения Кирхгофа. Тепловое излучение является одним из трёх элементарных видов переноса тепловой энергии. Равновесное излучение — тепловое излучение, находящееся в термодинамическом равновесии с веществом. Основными количественными характеристиками теплового излучения являются:
энергетическая светимость тела в пределах каких-то длин волн вычисляется интегрированием Rλ,T = f(λ, T) для T = const:
коэффициент поглощения - отношение поглощенной телом энергии к падающей энергии. Так, если на тело падает излучение потока dФпад, то одна его часть отражается от поверхности тела - dФотр, другая часть проходит в тело и частично превращается в теплоту dФпогл, а третья часть после нескольких внутренних отражений - проходит через тело наружу dФпр: α = dФпогл/dФпад.
Закон Стефана — Больцмана — закон излучения абсолютно чёрного тела. Определяет зависимость мощности излучения абсолютно чёрного тела от его температуры. Формулировка закона:
где
где Численное значение Закон открыт независимо Й. Стефаном и Л. Больцманом в предположении пропорциональности плотности энергии излучения его давлению Важно отметить, что закон говорит только об общей излучаемой энергии. Распределение энергии по спектру излучения описывается формулой Планка, в соответствии с которой в спектре имеется единственный максимум, положение которого определяется законом Вина. Закон излучения Кирхгофа. В современной формулировке з акон звучит следующим образом: Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы. Известно, что при падении электромагнитного излучения на некоторое тело часть его отражается, часть поглощается и часть может пропускаться. Доля поглощаемого излучения на данной частоте называется поглощательной способностью тела Величины
По определению, абсолютно чёрное тело поглощает всё падающее на него излучение, то есть для него Реальные тела имеют поглощательную способность меньшую единицы, а значит, и меньшую чем у абсолютно чёрного тела излучательную способность. Тела, поглощательная способность которых не зависит от частоты, называются серыми. Их спектримеет такой же вид, как и у абсолютно чёрного тела. В общем же случае поглощательная способность тел зависит от частоты и температуры, и их спектр может существенно отличаться от спектра абсолютно чёрного тела. Изучение излучательной способности разных поверхностей впервые было проведено шотландским ученым Лесли при помощи его же изобретения —куба Лесли.
4.2. Фотоэлектрическим эффектом (фотоэффектом) называется явление взаимодействия света с веществом, в результате которого энергия фотонов передается электронам вещества. Для твердых и жидких тел различается внешний и внутренний фотоэффект. При внешнем фотоэффекте поглощение фотонов сопровождается вылетом электронов за пределы тела. При внутреннем фотоэффекте электроны, вырванные из атомов, молекул и ионов, остаются внутри вещества, но изменяются энергии электронов. В газах фотоэффект состоит в явлении фотоионизации – вырывании электронов из атомов и молекул газа под действием света. Качественный вид вольт-амперной характеристики фотоэлемента, то есть зависимости фототока
Положительное напряжение соответствует ускоряющему электрическому полю, в которое попадают вылетающие из катода электроны. Поэтому, в области положительных напряжений все испускаемые катодом электроны достигают анода, обуславливая фототок насыщения Небольшой спад фототока при малых положительных напряжениях, который наблюдается в опытах, связан с контактной разностью потенциалов между катодом и анодом. Ниже, при обсуждении закономерностей фотоэффекта мы будем пренебрегать влиянием контактной разности потенциалов. При отрицательном напряжении При некотором отрицательном напряжении, величину которого Измерив задерживающее напряжение, можно определить эту максимальную энергию или максимальную скорость
Экспериментально были установлены следующие основные закономерности фотоэффекта: 1. Для монохроматического света определенной длины волны фототок насыщения пропорционален световому потоку, падающему на катод. 2. Максимальная кинетическая энергия фотоэлектронов не зависит от величины светового потока, а определяется лишь частотой излучения. 3. Для каждого вещества катода существует своя граничная частота
Непосредственным следствием этого уравнения являются второй и третий законы фотоэффекта. Действительно, из (1.55) следует, что максимальная энергия фотоэлектронов зависит от частоты падающего на металл излучения. Кроме того, если
из которых следует, что эти характеристики полностью определяются значением работы выхода электрона из металла.
4.3. Фотон — элементарная частица, квант электромагнитного излучения (в узком смысле — света). Это безмассовая частица, способная существовать только двигаясь со скоростью света. Электрический заряд фотона равен нулю. Фотон может находиться только в двух спиновых состояниях с проекцией спина на направление движения (спиральностью) ±1. Этому свойству в классической электродинамике соответствует круговая правая и левая поляризация электромагнитной волны. Фотону как квантовой частице свойственен корпускулярно-волновой дуализм, он проявляет одновременно свойства частицы и волны. Фотоны обозначаются буквой Корпускулярно-волновой дуализм, Принцип неопределённости Гейзенберга Фотону свойственен корпускулярно-волновой дуализм. С одной стороны, фотон демонстрирует свойства электромагнитной волны в явлениях дифракции и интерференции в том случае, если характерные размеры препятствий сравнимы с длиной волны фотона. Например, последовательность одиночных фотонов с частотой
Мысленный эксперимент Гейзенберга по определению местонахождения электрона(закрашен синим) с помощью гамма-лучевого микроскопа высокого разрешения. Падающие гамма-лучи (показаны зелёным) рассеиваются на электроне и попадают в апертурный угол микроскопа θ. Рассеянные гамма-лучи показаны на рисунке красным цветом. Классическая оптика показывает, что положение электрона может быть определено только с точностью до определённого значения Δ x, которое зависит от угла θ и от длины волны λ падающих лучей. Ключевым элементом квантовой механики является принцип неопределённости Гейзенберга, который запрещает одновременное точное определение пространственной координаты частицы и её импульса по этой координате. Важно отметить, что квантование света и зависимость энергии и импульса от частоты необходима для выполнения принципа неопределённости, применённого к заряженной массивной частице. Иллюстрацией этого может служить знаменитый мысленный эксперимент с идеальным микроскопом, определяющим координату электрона путём облучения его светом и регистрации рассеянного света (гамма-микроскоп Гейзенберга). Положение электрона может быть определено с точностью
где Напротив, формула Эйнштейна для импульса фотона полностью удовлетворяет требованиям принципа неопределённости. С учётом того, что фотон может быть рассеян в любом направлении в пределах угла
После умножения первого выражения на второе получается соотношение неопределённостей Гейзенберга:
4.4. Опыты Резерфорда привели к выводу, что в центре атома находится плотное положительно заряженное ядро (атомное ядро, отсюда название модели), диаметр которого не превышает 10–14–10–15 м. Это ядро занимает только 10–12 часть полного объема атома, но содержит весь положительный заряд и не менее 99,95 % его массы. Веществу, составляющему ядро атома, следовало приписать колоссальную плотность порядка ρ ≈ 1015 г/см3. Заряд ядра должен быть равен суммарному заряду всех электронов, входящих в состав атома. Впоследствии удалось установить, что если заряд электрона принять за единицу, то заряд ядра в точности равен номеру данного элемента в таблице Менделеева.
Рисунок 6.1.3.Рассеяние α-частицы в атоме Томсона (a) и в атоме Резерфорда (b) В дальнейшем Резерфорд предложил планетарную модель атома. Согласно этой модели, в центре атома располагается положительно заряженное ядро, в котором сосредоточена почти вся масса атома. Атом в целом нейтрален. Вокруг ядра, подобно планетам, под действием кулоновских сил со стороны ядра вращаются электроны (рис. 6.1.4). Находиться в состоянии покоя электроны не могут, так как они упали бы на ядро.
Рис. 6.1.4.Планетарная модель атома Резерфорда.Показаны круговые орбиты четырех электронов
4.5. Атомное ядро — центральная часть атома, в которой сосредоточена основная его масса(более 99,9 %). Ядро заряжено положительно, заряд ядра определяет химический элемент, к которому относят атом. Размеры ядер различных атомов составляют несколько фемтометров, что в более чем в 10 тысяч раз меньше размеров самого атома. Атомное ядро состоит из нуклонов — положительно заряженных протонов и нейтральных нейтронов, которые связаны между собой при помощи сильного взаимодействия. Количество протонов в ядре называется его зарядовым числом Деление представляет собой распад (расщепление) атомного ядра на две прибл. равные части (осколки), сопровождающийся выделением энергии и, в отд. случаях, испусканием одной или неск. частиц, напр, нейтронов. Нек-рые тяжелые ядра могут делиться самопроизвольно (спонтанно), более легкие - в случае соударения с др. ядрами, обладающими большой энергией. Кроме того, тяжелые ядра, напр, атомов урана, способны делиться под воздействием бомбардировки нейтронами, а поскольку при этом испускаются новые нейтроны, процесс может стать самоподдерживающимся, т.е. возникает цепная реакция. В ходе такой реакции деления происходит высвобождение большого кол-ва энергии. В ядерных реакторах протекают управляемые цепные реакции, а в атомной бомбе - неуправляемые. Синтезом называется слияние ядер двух легких атомов с образованием нового ядра, соответствующего более тяжелому атому. Если это новое ядро стабильно, то при синтезе выделяется энергия, поскольку связи в нем оказываются более прочными, чем в исходных ядрах. От хим. реакций ядерный синтез отличается участием в нем не только электронов атомов, но и их ядер. На единицу массы реагирующих в-в в реакции синтеза ядер выделяется прибл. в 10 раз больше энергии, чем в реакциях деления. Синтез ядер идет в центр, области Солнца и др. звезд, являясь источником их энергии. Неуправляемая реакция такого синтеза реализуется в водородных бомбах. В наст, время ведутся исследования по осуществлению управляемых реакций подобного синтеза в кач-ве источников энергии.
4.6. Элементарная частица — собирательный термин, относящийся к микрообъектам в субъядерном масштабе, которые невозможно расщепить на составные части. Следует иметь в виду, что некоторые элементарные частицы (электрон, фотон, кварки и т. д.) на данный момент считаются бесструктурными и рассматриваются как первичные фундаментальные частицы. Другие элементарные частицы (так называемые составные частицы — протон, нейтрон и т. д.) имеют сложную внутреннюю структуру, но, тем не менее, по современным представлениям, разделить их на части невозможно. Фундаментальная частица — бесструктурная элементарная частица, которую до настоящего времени не удалось описать как составную. В настоящее время термин применяется преимущественно для лептонов и кварков (по 6 частиц каждого рода, вместе с античастицами, составляют набор из 24 фундаментальных частиц) в совокупности с калибровочными бозонами(частицами-переносчиками фундаментальных взаимодействий).
4.7. Молекулярно-кинетическая теория истолковывает свойства тел, которые непосредственно наблюдаются на опыте (давление, температуру и т.п.), как суммарный результат действия молекул. При этом она пользуется статистическим методом, интересуясь не движением отдельных молекул, а лишь средними величинами, которые характеризуют движение огромной совокупности частиц. Отсюда другое её название – статистическая физика. 4.8. Термодинамические параметры - температура, плотность, давление, объем, удельное электрическое сопротивление и другие физические величины: На основании использования основных положений молекулярно-кинетической теории было получено основное уравнение МКТ идеального газа, которое выглядит так: В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Средняя энергия движения одной молекулы равна Учитывая, что Для любой массы m газа, т.е. для любого числа киломолей
Из этого выражения следует, что внутренняя энергия является однозначной функцией состояния и, следовательно, при совершении системой любого процесса, в результате которого система возвращается в исходное состояние, полное изменение внутренней энергии равно нулю. Математически это записывается в виде тождества Второе начало термодинамики утверждает, что все необратимые процессы (а такими являются практически все тепловые процессы, во всяком случае, все естественно протекающие процессы) идут так, что энтропия участвующих в них тел возрастает, стремясь к максимальному значению. Максимальное значение энтропии достигается тогда, когда система приходит в равновесное состояние. Вместе с тем выше уже отмечалось, что переход к равновесному состоянию является значительно более вероятным по сравнению со всеми другими переходами. Поэтому и наблюдаются только те изменения состояния, при которых система переходит из менее вероятного в более вероятное состояние (термодинамическая вероятность возрастает). Связь между термодинамической вероятностью состояния системы и ее энтропией была установлена в 1875 г. двумя знаменитыми учеными – Д. Гиббсом и Л. Больцманом. Эта связь выражается формулой Больцмана, которая имеет вид:
где
4.9. Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнениеМенделеева — Клапейрона) — формула, устанавливающая зависимость междудавлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
где
Так как
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона. В случае постоянной массы газа уравнение можно записать в виде:
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса. Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия Уравнение состояния Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой. Для одного моля газа Ван-дер-Ваальса оно имеет вид:
где
Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка Для
Изотерма линия на диаграмме состояния, изображающая процесс, происходящий при постоянной температуре (изотермический процесс). Уравнение Изотерма идеального газа pV = const, где р — давление, V — объём газа. Для реального газа уравнение Изотерма имеет более сложный характер и переходит в уравнение Изотерма идеального газа только при малых давлениях или высоких температурах. На рис. 2.8 схематически изображены изотермы газа Ван-дер-Ваальса для различных температур.
На этих изотермах хорошо просматривается участок, где давление растёт с ростом объёма. Этот участок не имеет физического смысла. В области, где изотерма делает зигзагообразный изгиб, изобара пересекает её три раза, то есть, имеется три значения объёма Критические параметры
Поскольку весь процесс происходит при постоянной температуре T, кривую, что изображает зависимость давления р от объёма V, называют изотермой. При объёме V1 начинается конденсация газа, а при объёме V2 она заканчивается. Если V > V1 то вещество будет в газообразном состоянии, а при V < V2 — в жидком. Опыты показывают, что такой вид имеют изотермы и всех других газов, если их температура не очень высокая. В этом процессе, когда газ превращается в жидкость при изменении его объёма от V1 к V2, давление газа остаётся постоянным. Каждой точке прямолинейной части изотермы 1—2 соответствует равновесие между газообразным и жидким состояниями вещества. Это означает, что при определённых T и V количество жидкости и газа над ней остаётся неизменным. Равновесие имеет динамический характер: количество молекул, которые покидают жидкости, в среднем равняется количеству молекул, которые переходят из газа в жидкость за одно и то же время. Также существует такое понятие как критическая температура, если газ находится при температуре выше критической (индивидуальна для каждого газа, например для углекислого газа примерно 304 К), то его уже невозможно превратить в жидкость, какое бы давление к нему не прилагалось. Данное явление возникает вследствие того, что при критической температуре силы поверхностного натяжения жидкости равны нулю. Если продолжать медленно сжимать газ при температуре большей критической, то после достижения им объёма, равного приблизительно четырем собственным объёмам молекул, составляющих газ, сжимаемость газа начинает резко падать.
4.10. Внутренняя энергия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в коне
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.19.89 (0.018 с.) |





 - степень черноты (для всех веществ
- степень черноты (для всех веществ  , для абсолютно черного тела
, для абсолютно черного тела  ). При помощи закона Планка для излучения, постоянную
). При помощи закона Планка для излучения, постоянную  можно определить как
можно определить как
 — постоянная Планка,
— постоянная Планка,  — постоянная Больцмана,
— постоянная Больцмана,  — скорость света.
— скорость света. Дж·с−1·м−2 · К−4.
Дж·с−1·м−2 · К−4. . В 1880 г. подтверждён Лео Гретцем.
. В 1880 г. подтверждён Лео Гретцем. . С другой стороны, каждое нагретое тело излучает энергию по некоторому закону
. С другой стороны, каждое нагретое тело излучает энергию по некоторому закону  , именуемым излучательной способностью тела.
, именуемым излучательной способностью тела.
 . Поэтому функция
. Поэтому функция  совпадает с излучательной способностью абсолютно чёрного тела, описываемой законом Стефана — Больцмана, вследствие чего излучательная способность любого тела может быть найдена исходя лишь из его поглощательной способности.
совпадает с излучательной способностью абсолютно чёрного тела, описываемой законом Стефана — Больцмана, вследствие чего излучательная способность любого тела может быть найдена исходя лишь из его поглощательной способности. от напряжения
от напряжения  между катодом и анодом для случая неизменного светового потока, падающего на катод, представлена на рис. 1.13.
между катодом и анодом для случая неизменного светового потока, падающего на катод, представлена на рис. 1.13.
 .
. испущенный катодом электрон попадает в тормозящее электрическое поле, преодолеть которое он может лишь имея определенный запас кинетической энергии. Электрон с малой кинетической энергией, вылетев из катода, не может преодолеть тормозящее поле и попасть на анод. Такой электрон возвращается на катод, не давая вклада в фототок. Поэтому, плавный спад фототока в области отрицательных напряжений указывает на то, что вылетающие из катода фотоэлектроны имеют разные значения кинетической энергии.
испущенный катодом электрон попадает в тормозящее электрическое поле, преодолеть которое он может лишь имея определенный запас кинетической энергии. Электрон с малой кинетической энергией, вылетев из катода, не может преодолеть тормозящее поле и попасть на анод. Такой электрон возвращается на катод, не давая вклада в фототок. Поэтому, плавный спад фототока в области отрицательных напряжений указывает на то, что вылетающие из катода фотоэлектроны имеют разные значения кинетической энергии. называют задерживающим напряжением (потенциалом), фототок становится равным нулю. Соответствующее тормозящее электрическое поле при этом задерживает все вылетающие из катода электроны, включая электроны с максимальной кинетической энергией
называют задерживающим напряжением (потенциалом), фототок становится равным нулю. Соответствующее тормозящее электрическое поле при этом задерживает все вылетающие из катода электроны, включая электроны с максимальной кинетической энергией  .
. фотоэлектронов из соотношения
фотоэлектронов из соотношения .
.
 такая, что излучение с частотой
такая, что излучение с частотой  фотоэффекта не вызывает. Эту граничную частоту называют частотой красной границы фотоэффекта. По шкале длин волн ей соответствует длина волны красной границы
фотоэффекта не вызывает. Эту граничную частоту называют частотой красной границы фотоэффекта. По шкале длин волн ей соответствует длина волны красной границы  , такая, что фотоэффект из данного металла вызывает излучение лишь с меньшей длиной волны
, такая, что фотоэффект из данного металла вызывает излучение лишь с меньшей длиной волны  .
. (1.55) называют уравнением Эйнштейна для внешнего фотоэффекта. Здесь
(1.55) называют уравнением Эйнштейна для внешнего фотоэффекта. Здесь  - максимальная энергия фотоэлектронов.
- максимальная энергия фотоэлектронов. , то фотоэффект не должен наблюдаться. Отсюда, для частоты и длины волны красной границы фотоэффекта получаем простые формулы
, то фотоэффект не должен наблюдаться. Отсюда, для частоты и длины волны красной границы фотоэффекта получаем простые формулы
 , поэтому их часто называют гамма-квантами (особенно фотоны высоких энергий); эти термины практически синонимичны. С точки зрения Стандартной модели фотон является калибровочным бозоном. Виртуальные фотоны являются переносчиками электромагнитного взаимодействия, таким образом обеспечивая взаимодействие, например, между двумя электрическими зарядами. Фотон — самая распространённая по численности частица во Вселенной. На один нуклон приходится не менее 20 миллиардов фотонов.
, поэтому их часто называют гамма-квантами (особенно фотоны высоких энергий); эти термины практически синонимичны. С точки зрения Стандартной модели фотон является калибровочным бозоном. Виртуальные фотоны являются переносчиками электромагнитного взаимодействия, таким образом обеспечивая взаимодействие, например, между двумя электрическими зарядами. Фотон — самая распространённая по численности частица во Вселенной. На один нуклон приходится не менее 20 миллиардов фотонов. , проходящих через двойную щель, создают на экране интерференционную картину, которую можно описать уравнениями Максвелла. Тем не менее, эксперименты показывают, что фотоны излучаются и поглощаются целиком объектами, которые имеют размеры, много меньшие длины волны фотона (например, атомами), или вообще в некотором приближении могут считаться точечными (так же как, например, электроны). Таким образом, фотоны в процессах излучения и поглощения ведут себя как точечно подобные частицы. В то же время, это описание не является достаточным; представление о фотоне как о точечной частице, чья траектория вероятностно задана электромагнитным полем, опровергается корреляционными экспериментами с запутанными состояниями фотонов.
, проходящих через двойную щель, создают на экране интерференционную картину, которую можно описать уравнениями Максвелла. Тем не менее, эксперименты показывают, что фотоны излучаются и поглощаются целиком объектами, которые имеют размеры, много меньшие длины волны фотона (например, атомами), или вообще в некотором приближении могут считаться точечными (так же как, например, электроны). Таким образом, фотоны в процессах излучения и поглощения ведут себя как точечно подобные частицы. В то же время, это описание не является достаточным; представление о фотоне как о точечной частице, чья траектория вероятностно задана электромагнитным полем, опровергается корреляционными экспериментами с запутанными состояниями фотонов.
 , равной разрешающей способности микроскопа. Исходя из представлений классической оптики:
, равной разрешающей способности микроскопа. Исходя из представлений классической оптики:
 — апертурный угол микроскопа. Таким образом, неопределённость координаты
— апертурный угол микроскопа. Таким образом, неопределённость координаты  падающих лучей. Однако после рассеяния электрон приобретает некоторый дополнительный импульс, неопределённость которого равна
падающих лучей. Однако после рассеяния электрон приобретает некоторый дополнительный импульс, неопределённость которого равна  . Если бы падающее излучение не было квантованным, эту неопределённость можно было бы сделать сколь угодно малой, уменьшая интенсивность излучения. Длину волны и интенсивность падающего света можно менять независимо друг от друга. В результате при отсутствии квантования света стало бы возможным одновременно определить с высокой точностью положение электрона в пространстве и его импульс, что противоречит принципу неопределённости.
. Если бы падающее излучение не было квантованным, эту неопределённость можно было бы сделать сколь угодно малой, уменьшая интенсивность излучения. Длину волны и интенсивность падающего света можно менять независимо друг от друга. В результате при отсутствии квантования света стало бы возможным одновременно определить с высокой точностью положение электрона в пространстве и его импульс, что противоречит принципу неопределённости.
 . Таким образом, весь мир квантован: если вещество подчиняется законам квантовой механики, то и поле должно им подчиняться, и наоборот.
. Таким образом, весь мир квантован: если вещество подчиняется законам квантовой механики, то и поле должно им подчиняться, и наоборот.

 — это число равно порядковому номеру элемента, к которому относится атом в натуральном ряду элементов в таблице Менделеева. Количество протонов в ядре определяет структуру электронной оболочки нейтрального атома и, таким образом, химические свойства соответствующего элемента. Количество нейтронов в ядре называется его изотопическим числом
— это число равно порядковому номеру элемента, к которому относится атом в натуральном ряду элементов в таблице Менделеева. Количество протонов в ядре определяет структуру электронной оболочки нейтрального атома и, таким образом, химические свойства соответствующего элемента. Количество нейтронов в ядре называется его изотопическим числом  . Ядра с одинаковым числом протонов и разным числом нейтронов называются изотопами. Ядра с одинаковым числом нейтронов, но разным числом протонов — называются изотонами. Полное количество нуклонов в ядре называется его массовым числом
. Ядра с одинаковым числом протонов и разным числом нейтронов называются изотопами. Ядра с одинаковым числом нейтронов, но разным числом протонов — называются изотонами. Полное количество нуклонов в ядре называется его массовым числом  (
(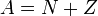 ) и приблизительно равно средней массе атома, указанной в таблице Менделеева. Нуклиды с одинаковым массовым числом, но разным протон-нейтронным составом принято называть изобарами. Как и любая квантовая система, ядра могут находиться в метастабильном возбуждённом состоянии, причём в отдельных случаях время жизни такого состояния исчисляется годами. Такие возбуждённые состояния ядер называются ядерными изомерами. Почти 90 % из 2500 известных атомных ядер нестабильны. Нестабильное ядро самопроизвольно превращается в другие ядра с испусканием частиц. Это свойство ядер называется радиоактивностью. Было выяснено, что радиоактивные ядра могут испускать частицы трех видов: положительно и отрицательно заряженные и нейтральные. Эти три вида излучений были названы α-, β- и γ-излучениями. Эти три вида радиоактивных излучений сильно отличаются друг от друга по способности ионизировать атомы вещества и, следовательно, по проникающей способности. Наименьшей проникающей способностью обладает α-излучение. В воздухе при нормальных условиях α-лучи проходят путь в несколько сантиметров. β-лучи гораздо меньше поглощаются веществом. Они способны пройти через слой алюминия толщиной в несколько миллиметров. Наибольшей проникающей способностью обладают γ-лучи, способные проходить через слой свинца толщиной 5–10 см.
) и приблизительно равно средней массе атома, указанной в таблице Менделеева. Нуклиды с одинаковым массовым числом, но разным протон-нейтронным составом принято называть изобарами. Как и любая квантовая система, ядра могут находиться в метастабильном возбуждённом состоянии, причём в отдельных случаях время жизни такого состояния исчисляется годами. Такие возбуждённые состояния ядер называются ядерными изомерами. Почти 90 % из 2500 известных атомных ядер нестабильны. Нестабильное ядро самопроизвольно превращается в другие ядра с испусканием частиц. Это свойство ядер называется радиоактивностью. Было выяснено, что радиоактивные ядра могут испускать частицы трех видов: положительно и отрицательно заряженные и нейтральные. Эти три вида излучений были названы α-, β- и γ-излучениями. Эти три вида радиоактивных излучений сильно отличаются друг от друга по способности ионизировать атомы вещества и, следовательно, по проникающей способности. Наименьшей проникающей способностью обладает α-излучение. В воздухе при нормальных условиях α-лучи проходят путь в несколько сантиметров. β-лучи гораздо меньше поглощаются веществом. Они способны пройти через слой алюминия толщиной в несколько миллиметров. Наибольшей проникающей способностью обладают γ-лучи, способные проходить через слой свинца толщиной 5–10 см. , где р — давление идеального газа, m0 — масса молекулы,
, где р — давление идеального газа, m0 — масса молекулы,  среднее значение концентрация молекул, квадрата скорости молекул.
среднее значение концентрация молекул, квадрата скорости молекул. получим основное уравнение МКТ идеального газа в виде:
получим основное уравнение МКТ идеального газа в виде: 
 . Так как в одном киломоле содержится
. Так как в одном киломоле содержится  молекул, то внутренняя энергия одного киломоля газа будет
молекул, то внутренняя энергия одного киломоля газа будет 
 , получим
, получим 
 внутренняя энергия
внутренняя энергия

 ,
,
 , R – универсальная газовая постоянная, NA – число Авогадро.
, R – универсальная газовая постоянная, NA – число Авогадро.
 — давление,
— давление, — молярный объём,
— молярный объём, — универсальная газовая постоянная
— универсальная газовая постоянная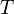 — абсолютная температура,К.
— абсолютная температура,К. , где
, где  , где
, где 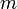 — масса,
— масса,  —молярная масса, уравнение состояния можно записать:
—молярная масса, уравнение состояния можно записать:


 — закон Бойля — Мариотта (изотрмический процесс)
— закон Бойля — Мариотта (изотрмический процесс) — Закон Гей-Люссака (изобарический).
— Закон Гей-Люссака (изобарический). — закон Шарля (второй закон Гей-Люссака, 1808 г., изохорический)
— закон Шарля (второй закон Гей-Люссака, 1808 г., изохорический) становится функцией не только температуры, но и объёма.
становится функцией не только температуры, но и объёма.
 — молярный объём,
— молярный объём, учитывает силы притяжения между молекулами (давление на стенку уменьшается, т.к. есть силы, втягивающие молекулы приграничного слоя внутрь), поправка
учитывает силы притяжения между молекулами (давление на стенку уменьшается, т.к. есть силы, втягивающие молекулы приграничного слоя внутрь), поправка  — силы отталкивания (из общего объёма вычитаем объём, занимаемый молекулами).
— силы отталкивания (из общего объёма вычитаем объём, занимаемый молекулами).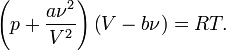 Где
Где  Рис. 2.8.Изотермы газа Ван-дер-Ваальса
Рис. 2.8.Изотермы газа Ван-дер-Ваальса
 при одинаковых значениях параметров
при одинаковых значениях параметров  и
и  . При повышении температуры волнообразный участок уменьшается и превращается в точку (см. точка К на рис. 2.8). Эта точка называется критической, а значения
. При повышении температуры волнообразный участок уменьшается и превращается в точку (см. точка К на рис. 2.8). Эта точка называется критической, а значения  ,
,  и
и  в этой точке называются критическими параметрами. При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями
в этой точке называются критическими параметрами. При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями  .
. можно найти из условия, что в критической точке изотерма Ван-дер-Ваальса имеет как экстремум, так и точку перегиба. Таким образом, из уравнения состояния газа Ван-дер-Ваальса следует существование у реальных газов критической точки с параметрами
можно найти из условия, что в критической точке изотерма Ван-дер-Ваальса имеет как экстремум, так и точку перегиба. Таким образом, из уравнения состояния газа Ван-дер-Ваальса следует существование у реальных газов критической точки с параметрами  Изотермы реального газа (схематично)
Изотермы реального газа (схематично)


