
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изменение энтропии в изопроцессахСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
4.12. Процесс, при котором система переходит из состояния 1 в состояние 2, а затем возвращается в состояние 1 через другие промежуточные процессы, называется круговым процессом или циклом. Графически цикл изображается замкнутой кривой. Всякая тепловая машина представляет собой систему, совершающую много кратно некий круговой процесс (цикл). Пусть в ходе цикла рабочее вещество (например, газ) сначала расширяется до объёма
где
Как следует из этого выражения, не вся получаемая извне теплота
Коэффициентом полезного действия
Цикл Карно и его КПД Французский инженер Сади Карно предложил идеальный цикл, который даёт максимальное КПД т.е.
Вычислим КПД цикла Карно для идеального газа. При изотермическом процессе внутренняя энергия идеального газа остаётся постоянной. Поэтому количество полученной газом теплоты
где Количество отдаваемой холодильнику теплоты
Для того чтобы цикл был замкнутым, состояние 1 и 4 должны лежать на одной и той же адиабате. Отсюда вытекает условие Аналогично для состояний 2 и 3 должно вытекать условие Разделив одно соотношение на другое, приходим к условию замкнутости цикла Теперь подставляя
В результате получим формулу для КПД цикла Карно:
где Вернёмся к соотношению (2), которое имеет место в случае обратимого цикла Карно. В общем случае при возможности необратимог о цикла Карно это соотношение примет вид:
Преобразуем (3) следующим образом:
В результате получим Для обратимого цикла Карно: для необратимого цикла Карно: Для произвольного обратимого цикла:
для произвольного необратимого цикла:
4.13. Обратимым процессом называют такой процесс, который может быть проведен в обратном направлении таким образом, что система будет проходить через те же состояния, что и при прямом ходе, но в обратной последовательности. Обратимым может быть только равновесный процесс.
Обратимый процесс обладает следующими свойствами: если при прямом ходе на каком-то элементарном участке (рис. 9.8.) система получает тепло В том случае, когда после завершения прямого и обратного процессов система вернулась в первоначальное состояние и в окружающей среде остались изменения, процесс является необратимым. Очевидно, что все процессы в природе необратимые.
Необратимость тепловых процессов находит свое выражение во втором законе термодинамики. Второй з-н термодинамики указывает направление возможных энергетических превращений и тем самым выражает необратимость процессов в природе.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 825; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.117.94 (0.011 с.) |

 .
.
 ,
,
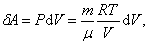 ,
,
 , или
, или
 .
.
 , т.к.
, т.к.  ;
;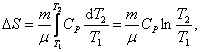 т.к. Р1 = Р2;
т.к. Р1 = Р2; т.к.
т.к.  ;
; , т.к.
, т.к. 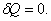
 .
. , а затем сжимается до первоначального объёма
, а затем сжимается до первоначального объёма  (рис. 1). Чтобы работа за цикл была больше нуля, давление, (а, следовательно, и температура) в процессе расширения должно быть больше, чем при сжатии. Для этого рабочему веществу нужно в ходе расширения сообщать теплоту, а в ходе сжатия отнимать от него теплоту. Совершив цикл, рабочее вещество возвращается в исходное состояние. Поэтому изменение внутренней энергии за цикл равно нулю. Количество теплоты, сообщаемой рабочему телу за цикл, равно
(рис. 1). Чтобы работа за цикл была больше нуля, давление, (а, следовательно, и температура) в процессе расширения должно быть больше, чем при сжатии. Для этого рабочему веществу нужно в ходе расширения сообщать теплоту, а в ходе сжатия отнимать от него теплоту. Совершив цикл, рабочее вещество возвращается в исходное состояние. Поэтому изменение внутренней энергии за цикл равно нулю. Количество теплоты, сообщаемой рабочему телу за цикл, равно ,
, – теплота, получаемая рабочим телом при расширении, а
– теплота, получаемая рабочим телом при расширении, а  – теплота, отдаваемая при сжатии. Работа
– теплота, отдаваемая при сжатии. Работа  , совершаемая за цикл, равна площади цикла. Таким образом, первое начало термодинамики, написанное для цикла, имеет вид
, совершаемая за цикл, равна площади цикла. Таким образом, первое начало термодинамики, написанное для цикла, имеет вид . (1)
. (1) используется для получения полезной работы.
используется для получения полезной работы.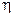 (сокращённо КПД) тепловой машины называется отношение совершаемой за цикл работы
(сокращённо КПД) тепловой машины называется отношение совершаемой за цикл работы  .
. . Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно.
. Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно. - изотермическое расширение при
- изотермическое расширение при  ,
,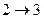 - адиабатическое расширение,
- адиабатическое расширение, 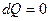 ,
, - изотермическое сжатие при
- изотермическое сжатие при  ,
, - изотермическое сжатие,
- изотермическое сжатие, 
 , совершаемой газом при переходе из состояния 1 в состояние 2 (рис. 2). Эта работа равна
, совершаемой газом при переходе из состояния 1 в состояние 2 (рис. 2). Эта работа равна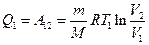 ,
, – масса идеального газа в тепловой машине.
– масса идеального газа в тепловой машине. равно работе
равно работе  , затраченной на сжатие газа при переходе его из состояния 3 в состояние 4. Эта работа равна
, затраченной на сжатие газа при переходе его из состояния 3 в состояние 4. Эта работа равна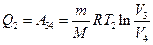 .
. .
. .
. .
. . (2)
. (2) ,
, . (3)
. (3) ,
,  , или
, или 
 .
. ,
, .
.


 и совершает работу
и совершает работу  , то при обратном ходе на том же участке система отдает тепло
, то при обратном ходе на том же участке система отдает тепло  и над ней совершается работа
и над ней совершается работа  . По этой причине после протекания обратимого процесса в одном, а затем в обратном направлении и возвращение системы в первоначальное состояние в окружающих телах не должно оставаться никаких изменений. Например шарик на пружине в вакууме колеблется бесконечно долго.
. По этой причине после протекания обратимого процесса в одном, а затем в обратном направлении и возвращение системы в первоначальное состояние в окружающих телах не должно оставаться никаких изменений. Например шарик на пружине в вакууме колеблется бесконечно долго.



