
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энтропия в статистической физике.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Мы вводили понятие энтропии, используя определение, предложенное Клайпероном
равенство для обратимого процесса, неравенство – для любого необратимого процесса. Уже на этом этапе можно было бы получить важную теорему Больцмана о неубывании энтропии в замкнутой системе. Правда, только для частного случая адиабатных процессов. Действительно, при адиабатном процессе Обобщение этой теоремы на случай любого термодинамического процесса в замкнутой системе можно провести с помощью эквивалентного определения энтропии, предложенного Больцманом. Термодинамическая система может находиться в разных состояниях. Для их описания Больцман предложил рассматривать безразмерную вероятность нахождения системы в данном состоянии, которую можно обозначить, например, как W. Если система может находиться в K состояниях, то для данного состояния i вероятность равна
где Такое определение веса статистического состояния подразумевает, что состояния системы дискретны. Для случая непрерывного изменения состояний вместо
Основываясь на представлении о статистическом весе термодинамического состояния, Больцман определил энтропию соотношением (соотношение называется формулой Больцмана)
k – постоянная Больцмана (именно эта величина определяет размерность S), Изменение энтропии при переходе системы из состояния 1 в состояние 2 равно
Для бесконечно малого перехода, когда
Последняя формула может использоваться для описания сложных переходов в непрерывно изменяющихся термодинамических ансамблях. До сих пор мы рассматривали стационарные ансамбли, термодинамические потенциалы которых не зависят от времени. Такие ансамбли – часто встречающаяся идеализация физической картины. В настоящее время гораздо большее значение представляют статистические процессы, происходящие в неоднородных системах, и процессы с участие внешних сил. О неоднородных системах будет сказано позже. Для описания термодинамических и статистических процессов используются специальные методы. Примерами таких процессов могут служить процессы в лазерных полях (лазерная обработка – плавление, испарение, т.п.), возбуждение электрического тока в сложных проводящих системах, да и любые другие технологические процессы, и процессы передачи информации. Эти методы применимы в химии, биологии, экономике, медицине, метеорологии и многих других областях деятельности человека. Речь идет о кинетических уравнениях, которые дают описание динамики изменения различных термодинамических потенциалов во времени. Чаще всего используется кинетическое уравнение для функции распределения частиц по какому-либо параметру. Первым таким уравнением следует считать кинетическое уравнение Больцмана, которое можно записать для распределения частиц по энергиям в виде
Приведенное кинетическое уравнение записано в сжатом виде (не раскрыты функции G и Р, имеющие разный вид для разных кинетических процессов). Но уже сейчас видно, что это очень сложное уравнение, решение которого представляет значительные трудности. На основе кинетического уравнения Больцмана впервые была строго математически доказана теорема Больцмана о неубывании энтропии в замкнутой статистической системе и, тем самым, дано подтверждение Второму началу термодинамики. Подобные кинетические уравнения позволяют рассчитать значения флуктуаций. По определению, флуктуацией термодинамической величины
Расчет квадратичной флуктуации иногда бывает очень сложным. Такой расчет может дать вероятность ЧУДА, кода весь воздух соберется в одной половине аудитории, или когда монета упадет одной и той же стороной большее число раз, чем половина попыток. Флуктуации имеются как в стационарных системах, так и в системах, у которых параметры зависят от времени. Флуктуации всегда зависят от времени. В стационарных системах они возникают и затем «рассасываются». В нестационарных системах они имеют иной вид и иначе зависят от времени. В частности, они могут оказаться стационарными (ток заряженных частиц во внешнем электрическом поле; в этом случае
Процессы переноса. Если в равновесном ансамбле возникает флуктуация или на ансамбль оказывается внешнее воздействие, делающее ансамбль неоднородным, в нем возникают процессы переноса. Большинство из них (особенно при кратковременном внешнем воздействии) характеризуются временем релаксации или средним временем жизни флуктуации. Чтобы последовательно найти эти величины требуется их изучение с помощью кинетического уравнения. В самом простом случае (метод или приближение Блоха) производная в левой части кинетического уравнения заменяется отношением
где
Такой тип релаксации называют экспоненциальным. «Рассасывание» флуктуаций обычно происходит именно по такому закону. В других случаях релаксация может происходить другим, иногда весьма экзотическим образом. В любом случае рассасывание есть необратимый процесс, сопровождающийся увеличением энтропии. С понятием времени релаксации связано (но не совпадает с ним ни по смыслу, ни по величине) понятие среднего времени между столкновениями частиц, обычно обозначаемое как
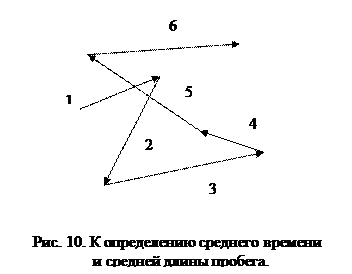
Обычно Аналогичным образом вводится средняя длина свободного пробега (см. рисунок 10). Цифры на рисунке 10 обозначают интервалы времени
Если рассматривать атомы или молекулы как шарики с диаметром d, то можно ввести газокинетическое поперечное сечение, равное площади круга
где Сечение определяется путем сложных квантовомеханических расчетов или по данным экспериментов. Если взять отношение
Эту формулу можно получить, используя распределение Максвелла по модулям скоростей,
Введённые средние величины используются для описания процессов переноса, среди которых основное значение имеют процесс переноса вещества – диффузия, процесс переноса энергии – теплопроводность, процесс переноса импульса – вязкость или внутреннее трение. Диффузия приводит к установлению равновесного пространственного распределения частиц. Для одномерного случая она подчиняется первому закону Фика
Здесь D – коэффициент диффузии (размерность Второй закон Фика рассматривает диффузию как процесс во времени. Для изотропной модели он имеет вид
Здесь введен оператор Лапласа
Диффузию часто характеризуют плотностью потока диффундирующего вещества (вектор)
Поток указывает, куда и какое количество вещества переносится за единицу времени через единичную поверхность. Строго говоря, пока речь шла о самодиффузии, связанной только с неоднородностью ансамбля из одинаковых частиц (её можно наблюдать, введи радиоактивные изотопы данных частиц). Подобным же образом происходит диффузия в смесях частиц или в твердых телах, в неоднородном поле температуры (термодиффузия), в неоднородном поле давления (бародиффузия), диффузия в различных внешних полях – электрическом, магнитном, световом. Для коэффициента самодиффузии статистическая теория дает
Похожим образом проводится описание теплопереноса. В изотропной среде для этого используется уравнение Фурье, являющееся следствием закона сохранения энергии при её кинетическом рассмотрении. В одномерном стационарном случае это уравнение имеет вид
здесь Кинетическая теория дает
где Полное уравнение теплопроводности в однородной изотропной системе, носящее специальное название «уравнение температуропроводности», имеет вид
где температура Наконец, внутреннее трение или вязкость связана с законом сохранения импульса и возникает из-за трения между условно выделенными слоями жидкости или газа при их параллельном движении с различными скоростями. Импульс передается от слоя к слою перпендикулярно направлению движения слоев. В стационарной системе при движении частиц вдоль оси у для описания вязкости используют уравнение Ньютона
По элементарной кинетической теории
Движение сферически симметричного тела радиусом R в вязкой жидкости было рассмотрено Стоксом, который получил следующее выражение для модуля силы вязкости
Вектор силы вязкости направлен против направления скорости, так что
Рекомендованная литература 1. Сивухин Д.В. Общий курс физики. Механика. – М.: «Наука», 2005. 2. Орир Дж. Физика: В 2 т. Т. 1. – М.: «Мир», 1981. 3. Сивухин Д.в. Общий курс физики. Термодинамика. 4. Стрекалов В.Н. Механика: конспект лекций. – М.: МГТУ «СТАНКИН», 1998. 5. Сайт www.vikipedia.ru 6. Стрекалов В.Н. Механика: методические указания к решению задач.– М.: МГТУ «СТАНКИН», 2010.
Вопросы к экзамену. Часть I. Механика. 1. Механическое движение. 2. Система отсчета. Система координат. Радиус вектор. Орты. 3. Система СИ. Основные механические единицы. 4. Материальная точка. 5. Средняя и мгновенная скорости. 6. Среднее и мгновенное ускорения. 7. Импульс и сила. 8. Кинетическая, потенциальная, полная механическая энергии. 9. Состояние механической системы. 10. Число степеней свободы. 11. Основная задача механики. 12. Закон Всемирного тяготения. 13. Физический смысл Первого закона Ньютона. 14. Три формы записи Второго закона Ньютона. 15. Решение основной задачи механики «в квадратурах». Роль начальных условий. 16. Третий закон Ньютона. 17. Плоское криволинейное движение. 18. Нормальное и тангенциальное ускорения. Их физический смысл. 19. Закон сохранения импульса. 20. Центр масс. Теорема о движении и центра масс. 21. Элементарная работа. Работа произвольной силы при произвольном перемещении. 22. Понятия «консервативная» и «неконсервативная» силы. Примеры. 23. Потенциальная энергия (материальная точка в поле тяжести и на пружине). 24. Закон сохранения механической энергии. 25. Всеобщий закон сохранения энергии. 26. Принцип относительности Галилея. 27. Принцип относительности Эйнштейна. 28. Преобразования Лоренца. 29. Материальная точка на пружине как пример гармонического осциллятора. 30. Уравнение движения гармонического осциллятора, его решение. Параметры осциллятора. 31. Слабозатухающий осциллятор с вязким трением. Уравнение движения. 32. Закон движения затухающего осциллятора. Параметры затухания. 33. Вынужденные колебания. Резонанс. 34. Момент инерции материальной точки, системы точек, твердого тела. 35. Понятие абсолютно твердого тела. Адитивность моментов инерции. 36. Моменты инерции обруча, диска, стержня. 37. Теорема Штейнера. 38. Момент силы, момент импульса. Плечо силы. Правила вычисление моментов. 39. Вывод уравнения моментов. 40. Основной закон вращательного движения абсолютно твердого тела. 41. Условия равновесия абсолютно твердого тела. 42. Закон сохранения момента импульса. 43. Вывод формулы для периода колебаний физического маятника. 44. Физический маятник (условия). Приведенная длина физического маятника. 45. Кинетическая энергия абсолютно твердого тела. 46. Идеальная жидкость. 47. Уравнение неразрывности (непрерывности). 48. Уравнение Бернулли.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 828; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.105 (0.013 с.) |

 ,
, , то есть
, то есть  .
. ,
, – число реализаций i-го состояния (например, если на кубике вместо числа 6 второй раз стоит число 3, то
– число реализаций i-го состояния (например, если на кубике вместо числа 6 второй раз стоит число 3, то  и вероятность появления тройки равна
и вероятность появления тройки равна 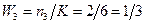 ). Число
). Число  и условие нормировки
и условие нормировки ,
, .
. ,
, учитывает, что энтропия определена с точностью до произвольной постоянной.
учитывает, что энтропия определена с точностью до произвольной постоянной. .
.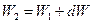 , находим
, находим .
. .
. – вероятность перехода в единицу времени из состояния 2 в состояние 1,
– вероятность перехода в единицу времени из состояния 2 в состояние 1,  – вероятность перехода из состояния 1 в состояние 2, эти функции учитывают внешние воздействия или просто упругие столкновения частиц,
– вероятность перехода из состояния 1 в состояние 2, эти функции учитывают внешние воздействия или просто упругие столкновения частиц,  – функция, которая учитывает закон сохранения энергии
– функция, которая учитывает закон сохранения энергии  .
. называют разность
называют разность  , где
, где  – среднее статистическое значение. Поскольку
– среднее статистическое значение. Поскольку  может изменять знак, то
может изменять знак, то  и «линейная» флуктуация малоинформативна. Обычно изучают квадратичные флуктуации,
и «линейная» флуктуация малоинформативна. Обычно изучают квадратичные флуктуации, .
. ).
). ,
, – время релаксации. Достаточно часто оказывается, что
– время релаксации. Достаточно часто оказывается, что .
. . Пусть столкновения происходят через некоторые интервалы времени
. Пусть столкновения происходят через некоторые интервалы времени  , где
, где  – число учтенных столкновений, следующих одно за другим. Тогда среднее время свободного пробега определяется стандартным образом:
– число учтенных столкновений, следующих одно за другим. Тогда среднее время свободного пробега определяется стандартным образом: .
. , проходимые частицей до следующего столкновения. Средняя длина свободного пробега равняется скаляру
, проходимые частицей до следующего столкновения. Средняя длина свободного пробега равняется скаляру  .
.
 . Поперечное сечение характеризует вероятность столкновения частиц. С помощью распределения Максвелла можно найти, что
. Поперечное сечение характеризует вероятность столкновения частиц. С помощью распределения Максвелла можно найти, что ,
, – концентрация частиц, т.е. число частиц в единице объема.
– концентрация частиц, т.е. число частиц в единице объема. к
к  .
. .
. .
. ),
),  – плотность вещества (
– плотность вещества ( ),
),  – элементарная площадка, перпендикулярная оси х,
– элементарная площадка, перпендикулярная оси х,  – масса вещества, перенесенного через
– масса вещества, перенесенного через  . Знак «–» показывает, что вещество самопроизвольно переносится туда, где его меньше.
. Знак «–» показывает, что вещество самопроизвольно переносится туда, где его меньше. .
. .
.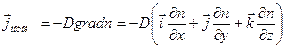 .
. .
. ,
, – коэффициент теплопроводности,
– коэффициент теплопроводности,  , знак «–» учитывает, что тепло
, знак «–» учитывает, что тепло  передается от более нагретой части системы к менее нагретой, через площадку
передается от более нагретой части системы к менее нагретой, через площадку  ,
, – удельная теплоемкость при постоянном объеме.
– удельная теплоемкость при постоянном объеме.
 ,
,  – коэффициент температуропроводности.
– коэффициент температуропроводности. ,
, – коэффициент вязкости с размерностью
– коэффициент вязкости с размерностью  ,
,  – сила, которая действует на поверхность
– сила, которая действует на поверхность  .
. .
. .
.


