
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет статистической теории информации.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Билеты по Теории Информации Оглавление Билет 1. 1 Билет 2. 3 Билет 3. 3 Билет 4. 3 Билет 5. 3 Билет 6. 12 Билет 7. 16 Билет 8. 16 Билет 9. 16 Билет 10. 18 Билет 11. 23 Билет 12. 25 Билет 13. 25 Билет 14. 28
Билет 1.
б) Определение симметричного канала и вычисление его пропускной способности
а)Модель статистической теории информации.
Понятие информация тождественно понятию сведения и ассоциирует с наличием по крайней мере двух взаимодействующих систем А и В, одна из которых В является наблюдаемой системой (приемником), а вторая А — источником информации. Вне указанной схемы понятие информация теряет смысл. Любая система описывается совокупностью физических величин, которые могут зависеть от параметров. Состояния системы — это значения физической величины или параметра, которые ее описывают. Если эти значения дискретны, то система называется дискретной, а если непрерывны, то система называется системой с непрерывным множеством состояний. Таким образом, в рамках прикладной теории информации, информация – это сведения о состоянии системы. Система случайным образом с некоторой вероятностью может оказаться в том или другом состоянии (передатчик приходит в состояние, которое соответствует передаваемой букве). Следовательно, множество состояний системы можно рассматривать как множество случайных событий. Две системы будем называть статистически зависимыми, если состояние одной из них влияет на вероятность состояния другой.
Предмет статистической теории информации. Теорией информации называется наука, изучающая количественные закономерности, связанные с получением, передачей, обработкой и хранением информации. б) Определение симметричного канала. Пропускная способность канала – предельная скорость передачи информации, при которой может быть получена сколь угодно малая вероятность ошибки. Канал называется симметричным, если он симметричен по входу и выходу. Для симметричного канала Н (У|Х)не зависит от распределения источника сообщений, поэтому пропускная способность Канал называется симметричным по входу, если строки матрицы различаются только порядком расстановки некоторого множества чисел Для симметричных по входу каналов частная условная энтропия Она не зависит от номера передаваемой буквы и может быть вычислена по любой строке матрицы. Поэтому условная энтропия Канал называется симметричным по выходу, если столбцы матрицы различаются только порядком расстановки некоторого множества чисел Если распределение источника равномерное ( Ценность информации
- Ценной информацией считается та информация, которая способствует достижению поставленной цели.
Один из способов измерения ценности информации, сформулированный в рамках статистической теории информации, был предложен А.А.Харкевичем. Ценность информации может быть выражена через приращение вероятности достижения цели. Если значение априорной вероятности достижения цели обозначить через р1, а апостериорной — через p2, то ценность полученной информации можно определить как log В системах передачи информации цель сводится к правильной передаче сообщений независимо от их конкретного содержания и формулируется относительно каждого символа множества X. Пусть целью является принятие решения в пользу xi. Тогда относительно этой цели ценность сведений,содержащихся в принятом yj равна log Таким образом, количество информации, которое уi несет об xi, равно
Умножая числитель и знаменатель под логарифмом на р{уj) и учитывая равенства p(xi|yj)p(yj)= p(xi, yj)= p(yj |xi)р(хi), получим
Отсюда следует, что yj несет об такое же количество информации, какое хi несет об yj (свойство симметрии). Поэтому I(хi, yj) называется взаимным количеством информации между i-м символом множества X и j-м символом множества У. Взаимное количество информации I(хi, yj), может быть положительным
Свойства энтропии Энтропия При равномерном распределении (pi= Докажем, что это максимальное значение энтропии. Используя равенство Н(Х)-logmX= Для оценки выражения log
Заменяя
где log e —модуль перехода. Отсюда
Пусть множество состоит из двух элементов, которые обозначим через единицу и ноль, причем единица появляется с вероятностью, равной р, а ноль — с вероятностью, равной q=1 — р. Тогда
Указанная зависимость изображена на рис. 1. Максимум достигается при p=q= 0,5. Билет 6.
а)Энтропия и её свойства. Энтропия которое необходимо для определения состояния одного разряда. Величина Из лабораторной 1: Предельные возможности определяются энтропией. Если она Энтропия: p- вер-ть появления еденицы в массиве Энтропия это количество информации которое приходится на один разряд. Из лабораторной 2: Проблема передачи непрер. сообщ-я закл. в получ. его копии на приемном пункте. Не сущ-ет способа, позвол-го получить точную копию перед-ого сообщ-я, поск. это требует бесконечной точности его воспроизв-я. Поэт. задают точность воспр-я перед-ого сообщ-я. воспр-я перед-ого сообщ-я. энтропия – это min кол-во инфы, кот. необх. передать по каналу, чт. восст. сообщение с заданной точностью Свойства энтропии Энтропия При равномерном распределении (pi= Докажем, что это максимальное значение энтропии. Используя равенство Н(Х)-logmX= Для оценки выражения log
Заменяя
где log e —модуль перехода. Отсюда
Пусть множество состоит из двух элементов, которые обозначим через единицу и ноль, причем единица появляется с вероятностью, равной р, а ноль — с вероятностью, равной q=1 — р. Тогда
Указанная зависимость изображена на рис. 1. Максимум достигается при p=q= 0,5.
б)Дискритизация непрерывных сообщений. Теорема Котельникова. Пространство сигналов. Произвольную кусочно-непрерывную функцию
если энергия функции Бесконечная система действительных функций
а отдельная функция
При заданной системе функций
достигает минимума. Минимум среднеквадратичной ошибки достигается в том случае, когда коэффициенты ряда определяются по формуле
Ряд, с определяемыми таким образом коэффициентами, называется обобщенным рядом Фурье. Ортогональная система называется полной, если путем увеличения количества членов в ряде среднеквадратичную ошибку можно сделать сколь угодно малой. Таким образом, по счетному множеству коэффициентов
Последнее равенство является обобщением теоремы Пифагора на случай n -мерного пространства. Путем непосредственных вычислений легко установить, что энергия сигнала
Таким образом, дискретизацией называется замена непрерывной функции Выбор системы ортогональных функций С целью передачи сигнала по каналу связи широко применяется разложение функции Согласно теореме Котельникова произвольная функция
образующие систему ортогональных функций, отличаются друг от друга только сдвигом по оси времени t на величину кратную
которую в результате тождественных преобразований можно привести к виду: Если дискретизации подлежит нормальный (гауссов) случайный процесс, энергетический спектр которого имеет прямоугольную форму, то коэффициенты Таким образом, непрерывные сообщения можно передавать в цифровом виде, то есть в виде последовательности чисел, при этом каждое число приближенно выражает величину соответствующего коэффициента
Билет 7. 1.Взаимная информация и её свойства. Источник информации и приемник можно рассматривать как подсистемы одной сложной системы. Взаимную информацию между состояниями подсистем, можно записать в виде
Поскольку сложная система случайным образом приходит в то или иное состояние, определяемое парой чисел (xi,yj), то I (xi,yj) будет случайной величиной, которую можно усреднить по всему множеству состояний. В результате почленного усреднения (4) получим выражение для средней (полной) взаимной информации:
где I(y,x)=
С точки зрения информационного описания системы связи безразлично, какую из подсистем рассматривать в качестве передатчика, а какую в качестве приемника. Поэтому энтропии Н (Х) и H (У) можно интерпретировать как информацию, которая поступает в канал связи, а условные энтропии H (X | Y), H (Y | X) как информацию, которая рассеивается в канале. В [1] доказано, что 1(Х, У)≥0. При выполнении указанного неравенства из (5) следует, что
Условную энтропию можно представить в виде
где величина
Таблица 1
При наличии статистической зависимости энтропия H (X | yj) может оказаться как меньше, так и больше Н (Х). Напомним, что для энтропии H (X | Y) всегда справедливо неравенство H (X | Y)≤ H (X). В качестве примера вычислим энтропии Н (Х), H (X | Y), H (X | yj) и взаимную информацию I (Х, У), когда системы А и В описываются двумерным распределением p (xi, yj), заданным в виде табл. 1. Вычисленные значения условной вероятности Используя записанные в таблицах значения вероятностей, полу чим
Отсюда
Билет. Алгоритм Шеннона-Фано.
Пусть имеется множество сообщений 1. Все сообщения располагаются в порядке убывания их вероятностей. 2. Упорядоченное множество сообщений делится на две части: верхнюю часть и нижнюю часть, причем так, чтобы разность между суммой вероятностей в верхней и нижней части была минимальной. 3. После этого сообщениям в верхней части ставится в соответствие 1, а в нижней – 0. 4. Далее аналогичные действия производятся с каждой из частей. Вновь полученные подмножества сообщений снова аналогичным образом делятся на две части и т.д., до получения по одному сообщению в каждом из подмножеств. 5. В результате каждому сообщению будет соответствовать своя последовательность из нулей и единиц, т.е. кодовое слово.
Пример:
Алгоритм Хаффмена.
1. Все сообщения располагаются в порядке убывания их вероятностей. 2. Два самых нижних сообщения объединяются в одно событие, вероятность которого равна сумме вероятностей, объединяемых событий, причем верхнему событию ставится в соответствие 1, а нижнему 0. 3. Получился новый массив сообщений с количеством состояний на единицу меньшим по сравнению с предыдущим массивом, если два последних события считать одним более крупным событием. Далее преобразуем этот массив в соответствии с пунктами 1 и 2. Полученный массив вновь подвергаем указанным преобразованиям и т.д. до тех пор, пока не будет исчерпан весь массив. 4. Геометрически результат можно представить в виде дерева, где кодовое слово, соответствующее
Пример:
x1=1, x2 = 01, x3 = 001, x4 = 000
б)Эпсилон-Энтропия. Производительность источника с непрерывным множеством состояний. ЭПСИЛОН - ЭНТРОПИЯ Проблема передачи непрерывного сообщения заключается в получении его копии на приемном пункте и, в сущности, сводится к процедуре воспроизведения сообщения на основе полученной информации. Очевидно, в данном случае не существует способа, позволяющего получить точную копию передаваемого сообщения, поскольку это требует бесконечной точности его воспроизведения, причем неограниченное увеличение точности требует неограниченного увеличения количества передаваемой информации. Например, нельзя получить два абсолютно совпадающих графика. Поэтому о передаче непрерывного сообщения имеет смысл говорить только в том случае, когда задана точность его воспроизведения. Передача непрерывного сообщения Пусть случайная величина Количество взаимной информации между множествами
равно энтропии Пронумеруем все элементы множества
Если величина Более универсальной мерой точности воспроизведения по сравнению с
которую при неравномерном распределении случайной величины Таким образом, количество информации, которое требуется для воспроизведения значения случайной величины Определим e - энтропию как минимальное по
Следует напомнить, что пропускная способность канала При квантовании непрерывной величины Отметим, что e - энтропия также используется и в качестве количественной меры производительности источника непрерывных сообщений, при этом, очевидно, нельзя говорить о производительности источника не задав точность воспроизведения. Таким образом, производительность источника можно определить как минимальное количество информации Кроме квантования существует много других способов преобразования непрерывной величины
где
Билет 11. Билет (сделала 2 варианта первого вопроса – по лекциям Ломакина и по методичке) Билет 14. 1. Определение скорости передачи информации и пропускной способности канала. Пропускная способность канала – предельная скорость передачи информации, при которой может быть получена сколь угодно малая вероятность ошибки. Для общего описания канала связи и построения теории информации используется одна и та же модель. Канал называется дискретным (непрерывным), если множества X и У дискретны (непрерывны), и полунепрерывным, если одно из множеств дискретно, а другое непрерывно. Ниже рассматриваются только дискретные каналы. Канал полностью описывается условными вероятностями Указанную вероятность можно рассматривать как функцию yjk и Определим скорость передачи информации как предел: Скорость передачи информации — скорость передачи данных, выраженная в количестве бит, символов или блоков, передаваемых за единицу времени. Скорость передачи информации R полностью определяется вероятностями р (хi)и р (yj | xi) ( В случае отсутствия помех Билеты по Теории Информации Оглавление Билет 1. 1 Билет 2. 3 Билет 3. 3 Билет 4. 3 Билет 5. 3 Билет 6. 12 Билет 7. 16 Билет 8. 16 Билет 9. 16 Билет 10. 18 Билет 11. 23 Билет 12. 25 Билет 13. 25 Билет 14. 28
Билет 1.
б) Определение симметричного канала и вычисление его пропускной способности
а)Модель статистической теории информации.
Понятие информация тождественно понятию сведения и ассоциирует с наличием по крайней мере двух взаимодействующих систем А и В, одна из которых В является наблюдаемой системой (приемником), а вторая А — источником информации. Вне указанной схемы понятие информация теряет смысл. Любая система описывается совокупностью физических величин, которые могут зависеть от параметров. Состояния системы — это значения физической величины или параметра, которые ее описывают. Если эти значения дискретны, то система называется дискретной, а если непрерывны, то система называется системой с непрерывным множеством состояний. Таким образом, в рамках прикладной теории информации, информация – это сведения о состоянии системы. Система случайным образом с некоторой вероятностью может оказаться в том или другом состоянии (передатчик приходит в состояние, которое соответствует передаваемой букве). Следовательно, множество состояний системы можно рассматривать как множество случайных событий. Две системы будем называть статистически зависимыми, если состояние одной из них влияет на вероятность состояния другой.
Предмет статистической теории информации. Теорией информации называется наука, изучающая количественные закономерности, связанные с получением, передачей, обработкой и хранением информации. б) Определение симметричного канала. Пропускная способность канала – предельная скорость передачи информации, при которой может быть получена сколь угодно малая вероятность ошибки. Канал называет
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.012 с.) |


 .
.

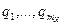 .
. ), то распределение р (уi)на выходе симметричного по выходу канала также будет равномерным. При этом энтропии H (X)и H (Y) достигают своего максимального значения(
), то распределение р (уi)на выходе симметричного по выходу канала также будет равномерным. При этом энтропии H (X)и H (Y) достигают своего максимального значения(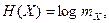
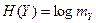 ).
). .
.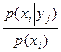 , где P(xi) — априорная вероятность передачи хi; p(xi|yj) — вероятность того, что было передано xi после принятия yj. При такой формулировке цели ценность информации совпадает с обычным количеством информации, которое определено выше.
, где P(xi) — априорная вероятность передачи хi; p(xi|yj) — вероятность того, что было передано xi после принятия yj. При такой формулировке цели ценность информации совпадает с обычным количеством информации, которое определено выше. .
. (3)
(3) , отрицательным
, отрицательным 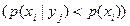 и равным нулю
и равным нулю  . Отрицательная информация называется дезинформацией.
. Отрицательная информация называется дезинформацией. поскольку pi удовлетворяет неравенству 0
поскольку pi удовлетворяет неравенству 0  1. Энтропия H(X)=0, когда система находится в одном из состояний с вероятностью, равной единице, и во всех остальных — с вероятностью, равной нулю. При этом имеется в виду, что
1. Энтропия H(X)=0, когда система находится в одном из состояний с вероятностью, равной единице, и во всех остальных — с вероятностью, равной нулю. При этом имеется в виду, что  pilog pi=0.
pilog pi=0. ) энтропия H(X)=logmx
) энтропия H(X)=logmx =1, можно выполнить следующие тождественные преобразования:
=1, можно выполнить следующие тождественные преобразования:
 воспользуемся неравенством lnz
воспользуемся неравенством lnz  z—1, положив z=
z—1, положив z= 
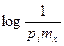 на
на  , получим
, получим

 .
. равна количеству информации,
равна количеству информации, является характеристикой источника сообщений и называется энтропией.
является характеристикой источника сообщений и называется энтропией. 1. Энтропия H(X)=0, когда система находится в одном из состояний с вероятностью, равной единице, и во всех остальных — с вероятностью, равной нулю. При этом имеется в виду, что
1. Энтропия H(X)=0, когда система находится в одном из состояний с вероятностью, равной единице, и во всех остальных — с вероятностью, равной нулю. При этом имеется в виду, что  ) энтропия H(X) max и определяется как H(X)=logmx
) энтропия H(X) max и определяется как H(X)=logmx
 воспользуемся неравенством lnz
воспользуемся неравенством lnz  на
на  , получим
, получим
 , изображающую сообщение или сигнал, можно разложить в обобщенный ряд Фурье по полной системе ортонормированных функций:
, изображающую сообщение или сигнал, можно разложить в обобщенный ряд Фурье по полной системе ортонормированных функций: ,
, конечна [9].
конечна [9]. называется ортогональной на отрезке [ a, b ], если
называется ортогональной на отрезке [ a, b ], если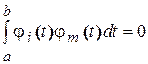 при
при 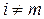 ,
, называется нормированной, если
называется нормированной, если .
. фиксированном числе членов ряда n значения коэффициентов
фиксированном числе членов ряда n значения коэффициентов  можно выбрать такими, при которых среднеквадратичная ошибка аппроксимации (аппроксимация - приближенное решение сложной функции с помощью более простых, что резко ускоряет и упрощает решение задач)
можно выбрать такими, при которых среднеквадратичная ошибка аппроксимации (аппроксимация - приближенное решение сложной функции с помощью более простых, что резко ускоряет и упрощает решение задач)
 .
. . Указанную последовательность можно интерпретировать как вектор в n - мерном Евклидовом пространстве с координатами
. Указанную последовательность можно интерпретировать как вектор в n - мерном Евклидовом пространстве с координатами 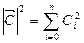 .
. .
.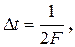 где F - верхняя граничная частота спектра сигнала. В этом случае функции
где F - верхняя граничная частота спектра сигнала. В этом случае функции ,
, , при этом каждая из них достигает своего максимального значения в те моменты времени, когда значения всех остальных функций равны нулю. Коэффициенты разложения определяются по формуле
, при этом каждая из них достигает своего максимального значения в те моменты времени, когда значения всех остальных функций равны нулю. Коэффициенты разложения определяются по формуле ,
, , то есть
, то есть 

 . (4)
. (4) ,
,
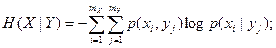


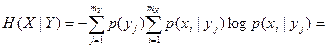

 называется частной условной энтропией. Она характеризует неопределенность состояния системы А в случае, когда известно состояние yj наблюдаемой системы В. Зафиксировав состояние yj системы В, мы тем самым изменяем комплекс условий, при которых может реализоваться событие xi. Это обнаруживается как изменение вероятности реализации события xi (i =
называется частной условной энтропией. Она характеризует неопределенность состояния системы А в случае, когда известно состояние yj наблюдаемой системы В. Зафиксировав состояние yj системы В, мы тем самым изменяем комплекс условий, при которых может реализоваться событие xi. Это обнаруживается как изменение вероятности реализации события xi (i =  ) (имеет место статистическая зависимость). Если до изменения условий указанная вероятность была равна безусловной (полной) вероятности p (Xi), то после изменения условий она стала равной условной вероятности p (xi | yj). При отсутствии статистической зависимости H (X | yj)= H (X), поскольку P (xi | yj)= p (xi).
) (имеет место статистическая зависимость). Если до изменения условий указанная вероятность была равна безусловной (полной) вероятности p (Xi), то после изменения условий она стала равной условной вероятности p (xi | yj). При отсутствии статистической зависимости H (X | yj)= H (X), поскольку P (xi | yj)= p (xi). X
y
X
y
 Таблица 2
Таблица 2 записаны в табл.2.
записаны в табл.2.








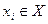 .
. выражается последовательностью дерева с соответствующим сообщением
выражается последовательностью дерева с соответствующим сообщением 
 сводится к передаче последовательности его значений взятых в дискретные моменты времени. Все возможные значения функции
сводится к передаче последовательности его значений взятых в дискретные моменты времени. Все возможные значения функции  .
. распределение. Тогда распределение дискретной случайной величины
распределение. Тогда распределение дискретной случайной величины 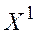 также будет равномерным, если все интервалы на которые разбит отрезок
также будет равномерным, если все интервалы на которые разбит отрезок  достигает своего максимального значения, равного
достигает своего максимального значения, равного  , где
, где  - число элементов в множестве
- число элементов в множестве  ,
, , с которой значение случайной величины
, с которой значение случайной величины  требуется количество информации, равное
требуется количество информации, равное  - ичной системе счисления. Минимальное количество разрядов
- ичной системе счисления. Минимальное количество разрядов 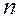 , некоторое при этом потребуется, удовлетворяет неравенству:
, некоторое при этом потребуется, удовлетворяет неравенству: .
. окажется целым числом, то количество информации, необходимое для воспроизведения значения случайной величины
окажется целым числом, то количество информации, необходимое для воспроизведения значения случайной величины 
 и их количество. Канал, устанавливающий связь между множествами
и их количество. Канал, устанавливающий связь между множествами  и, в сущности, представляет собой устройство квантования.
и, в сущности, представляет собой устройство квантования. источника:
источника:

 была определена как максимальное количество взаимной информации, но не по
была определена как максимальное количество взаимной информации, но не по  , то передача информации в виде чисел, записанных в
, то передача информации в виде чисел, записанных в  , не будет экономной. Поэтому целесообразно предварительно осуществить экономное кодирование сообщений, в роли которых должны выступать элементы множества
, не будет экономной. Поэтому целесообразно предварительно осуществить экономное кодирование сообщений, в роли которых должны выступать элементы множества  , необходимое в единицу времени для воспроизведения непрерывного сообщения
, необходимое в единицу времени для воспроизведения непрерывного сообщения  . Тогда при заданной дисперсии
. Тогда при заданной дисперсии  погрешности (при заданной среднеквадратичной ошибке) e - энтропия нормальной величины
погрешности (при заданной среднеквадратичной ошибке) e - энтропия нормальной величины  ,
, - дисперсия случайной величины
- дисперсия случайной величины  того, что k -мпринятым символом будет j -й символ множества Y (
того, что k -мпринятым символом будет j -й символ множества Y ( ).
). , вид которой отражает состояние канала, в частности, характер взаимодействия помехи и сигнала. Если
, вид которой отражает состояние канала, в частности, характер взаимодействия помехи и сигнала. Если 
 , (
, ( ) то соответствующий канал называется каналом без памяти. Если вероятность
) то соответствующий канал называется каналом без памяти. Если вероятность  где
где  средняя взаимная информация между переданным
средняя взаимная информация между переданным  и принятым
и принятым  . В случае отсутствия помех Н (Х|Y)=0, следовательно, R = Н (Х). Этот предел в случае канала без памяти равен взаимной информации: R=I(X, Y)=Н(Х)-Н(Х|Y)=Н(Y)-Н(Y|Х).
. В случае отсутствия помех Н (Х|Y)=0, следовательно, R = Н (Х). Этот предел в случае канала без памяти равен взаимной информации: R=I(X, Y)=Н(Х)-Н(Х|Y)=Н(Y)-Н(Y|Х). ). Поэтому изменять величину R мы можем только за счет изменения вида распределения р (хi), поскольку р (yj | xi)- характеристика неуправляемого канала. Определим пропускную способность канала С как максимальную по р (хi)скорость передачи информации:
). Поэтому изменять величину R мы можем только за счет изменения вида распределения р (хi), поскольку р (yj | xi)- характеристика неуправляемого канала. Определим пропускную способность канала С как максимальную по р (хi)скорость передачи информации: 




