
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пропускная способность гауссова канала связиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
R –информационная емкость регистра или mаx производительность источника. Т – время передачи сообщения
F- частота передачи сигнала N-шум x- входной сигнал \ состояние источника сообщения y-выходной сигнал \ мн-во состояний приемника
Канал будем называть гауссовым, если он удовлетворяет следующим условиям: 1) полоса пропускания канала ограничена частотой 2) шум в канале имеет нормальный (гауссов) закон распределения, 3) энергетический спектр шума равномерен в полосе пропускания канала и имеет значение, равное 4) мощность сигнала 5) сигнал 6) канал аддитивен, т. е. выходной сигнал
Пропускная способность канала определяется: 1) 2) Частная энтропия
где 3) Если отсчеты процесса
Согласно второй теореме К.Шеннона надежная передача сообщений в принципе возможна при
Билет 12.
Билет 13. Канал – совокупность технических средств между источником информации и потребителем информации. Пропускная способность канала – предельная скорость передачи информации, при которой может быть получена сколь угодно малая вероятность ошибки. Для общего описания канала связи и построения теории информации используется одна и та же модель. Канал называется дискретным (непрерывным), если множества X и У дискретны (непрерывны), и полунепрерывным, если одно из множеств дискретно, а другое непрерывно. Ниже рассматриваются только дискретные каналы. Канал полностью описывается условными вероятностями Указанную вероятность можно рассматривать как функцию yjk и Определим скорость передачи информации как предел: Скорость передачи информации R полностью определяется вероятностями р (хi)и р (yj | xi) ( В случае отсутствия помех
Введём пространство состояний системы с заданной на нём вероятностной мерой. Пронумеруем последовательность блоков(от 1 до n) так, что исправные будут помечаться 1, а не исправные 0, получим последовательность, которая будет описывать состояние системы. Всего таких состояний (последовательностей) будет 2n. Всё множество состояний S можно рассматривать как пространство элементарных событий
где pj - вероятность отказа j -го блока; J - множество номеров исправных блоков, I – множество номеров не исправленных блоков. При этом предполагается, что отказ одного из блоков не влияет на вероятность отказа других блоков. Возможна организация некоторой совокупности Z точек контроля, допустимое значение сигнала в каждой из которых обеспечивается определённым подмножеством блоков. В качестве исходной диагностической информации используется матрица проверок Bz, построенная на допустимом множестве точек контроля, где номер столбца совпадает с номером блока, а номер строки - с номером точки контроля. Проверка сигнала в каждой точке контроля позволяет судить о работоспособности всех блоков соответствующего подмножества, которое определяется совокупностью единиц в соответствующей строке матрицы проверок. Результат проверки принимается равным единице, если контролируемый сигнал вышел из допуска, и нулю в противном случае. Таким образом, при выходе из строя одного из блоков результат проверок совпадает с соответствующим столбцом матрицы. В случае выхода из строя нескольких блоков результаты проверок образуют вектор-столбец Таким образом, диагностический эксперимент доставляет некоторый вектор yi, который характеризует состояние системы с точностью до некоторого подмножества, причём вероятность p(yi) определяется как сумма вероятностей всех состояний, входящих в соответствующее подмножество. Разработку стратегии определения состояния системы будем вести с учётом следующих свойств этих подмножеств. Свойство 1. Подмножества, соответствующие разным векторам yi, не пересекаются. Действительно, если бы они пересекались, то нашлось бы такое состояние системы, которому соответствовали два различных вектора yi, чего быть не может. Свойство 2. Подмножество состояний замкнуто относительно операции сложения состояний. (Под суммой состояний будем понимать состояние, определяемое как многократный дефект, объединяющий дефекты суммируемых состояний). Свойство 3. Сумма всех состояний подмножества также принадлежит этому подмножеству. Свойство 4. Существует максимальное подмножество блоков, через отказы которых определяется всё подмножество состояний системы, соответствующее данному yi. Свойство 5. Каждому вектору yi соответствует подмножество подозреваемых в отказе блоков. Подмножества блоков, соответствующие разным векторам yi, могут пересекаться в отличие от соответствующих подмножеств состояний. Свойство 6. Максимальная кратность дефекта, который соответствует заданному yi, определяется количеством блоков в соответствующем подмножестве. Таким образом, стратегия определения состояния системы сводится к определению подмножества состояний, которое соответствует полученному вектору yi, а следовательно, и к определению подмножества блоков. Стратегия определения действительно неисправных блоков в подмножестве может быть различной. В частности, можно проверить каждый блок в отдельности, начиная с блоков, дефекты которых определяют наиболее вероятные состояния, к которым чаще всего относятся состояния с однократным дефектом.
Билет 14. Билет 14. 1. Определение скорости передачи информации и пропускной способности канала. Пропускная способность канала – предельная скорость передачи информации, при которой может быть получена сколь угодно малая вероятность ошибки. Для общего описания канала связи и построения теории информации используется одна и та же модель. Канал называется дискретным (непрерывным), если множества X и У дискретны (непрерывны), и полунепрерывным, если одно из множеств дискретно, а другое непрерывно. Ниже рассматриваются только дискретные каналы. Канал полностью описывается условными вероятностями Указанную вероятность можно рассматривать как функцию yjk и Определим скорость передачи информации как предел: Скорость передачи информации — скорость передачи данных, выраженная в количестве бит, символов или блоков, передаваемых за единицу времени. Скорость передачи информации R полностью определяется вероятностями р (хi)и р (yj | xi) ( В случае отсутствия помех
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 - энергия сигнала
- энергия сигнала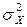 -мощность сигнала
-мощность сигнала - мощность шума
- мощность шума ,
, ,
, фиксирована и равна
фиксирована и равна  и шум
и шум  статистически независимы,
статистически независимы,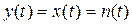 .
.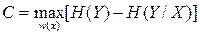
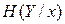 равна энтропии шума
равна энтропии шума 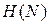 . Отсюда
. Отсюда  , а значение пропускной способности будет равно значению взаимной информации
, а значение пропускной способности будет равно значению взаимной информации  , которая определяется выражением
, которая определяется выражением [ бит/символ],
[ бит/символ],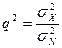 называется отношением сигнал/шум.
называется отношением сигнал/шум. на основании теоремы Котельникова выбрать с шагом
на основании теоремы Котельникова выбрать с шагом  , то за 1 секунду будет передано 2 F отсчетов. Пропускную способность можно записать:
, то за 1 секунду будет передано 2 F отсчетов. Пропускную способность можно записать: [бит/с].
[бит/с].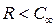 . то есть количество информации
. то есть количество информации  , которое надежно можно передать по каналу, должно быть меньше
, которое надежно можно передать по каналу, должно быть меньше 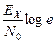 , где
, где  - энергия сигнала. Умножая неравенство на время передачи сообщения
- энергия сигнала. Умножая неравенство на время передачи сообщения 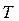 получим
получим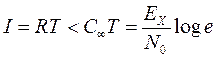
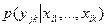 того, что k -мпринятым символом будет j -й символ множества Y (
того, что k -мпринятым символом будет j -й символ множества Y ( ).
). , вид которой отражает состояние канала, в частности, характер взаимодействия помехи и сигнала. Если
, вид которой отражает состояние канала, в частности, характер взаимодействия помехи и сигнала. Если 
 , (
, ( ) то соответствующий канал называется каналом без памяти. Если вероятность
) то соответствующий канал называется каналом без памяти. Если вероятность  где
где  средняя взаимная информация между переданным
средняя взаимная информация между переданным  и принятым
и принятым  . В случае отсутствия помех Н (Х|Y)=0, следовательно, R = Н (Х). Этот предел в случае канала без памяти равен взаимной информации: R=I(X, Y)=Н(Х)-Н(Х|Y)=Н(Y)-Н(Y|Х).
. В случае отсутствия помех Н (Х|Y)=0, следовательно, R = Н (Х). Этот предел в случае канала без памяти равен взаимной информации: R=I(X, Y)=Н(Х)-Н(Х|Y)=Н(Y)-Н(Y|Х). ). Поэтому изменять величину R мы можем только за счет изменения вида распределения р (хi), поскольку р (yj | xi)- характеристика неуправляемого канала. Определим пропускную способность канала С как максимальную по р (хi)скорость передачи информации:
). Поэтому изменять величину R мы можем только за счет изменения вида распределения р (хi), поскольку р (yj | xi)- характеристика неуправляемого канала. Определим пропускную способность канала С как максимальную по р (хi)скорость передачи информации: 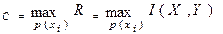

 , каждое из которых может наступить после эксплуатации системы в течение заданного времени с вероятностью, равной
, каждое из которых может наступить после эксплуатации системы в течение заданного времени с вероятностью, равной , (1)
, (1) , равный логической поэлементной сумме соответствующих столбцов матрицы, где Y - множество всех возможных исходов диагностического эксперимента, под которым будем понимать измерение сигналов в точке контроля.
, равный логической поэлементной сумме соответствующих столбцов матрицы, где Y - множество всех возможных исходов диагностического эксперимента, под которым будем понимать измерение сигналов в точке контроля. того, что k -мпринятым символом будет j -й символ множества Y (
того, что k -мпринятым символом будет j -й символ множества Y ( и принятым
и принятым 



