
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Адаптивная дискретизация непрерывных сообщений.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Произвольную кусочно-непрерывную функцию
если энергия функции Бесконечная система действительных функций
а отдельная функция
Система нормированных функций, в которой каждые две различающихся функции взаимно ортогональны, называется ортонормированной системой. При аппроксимации функции
достигает минимума. Минимум среднеквадратичной ошибки достигается в том случае, когда коэффициенты ряда определяются по формуле
Ряд, с определяемыми таким образом коэффициентами, называется обобщенным рядом Фурье. Ортогональная система называется полной, если путем увеличения количества членов в ряде среднеквадратичную ошибку можно сделать сколь угодно малой. Таким образом, по счетному множеству коэффициентов
Последнее равенство является обобщением теоремы Пифагора на случай n -мерного пространства. Путем непосредственных вычислений легко установить, что энергия сигнала
Таким образом, дискретизацией называется замена непрерывной функции Выбор системы ортогональных функций С целью передачи сигнала по каналу связи широко применяется разложение функции Согласно теореме Котельникова произвольная функция
образующие систему ортогональных функций, отличаются друг от друга только сдвигом по оси времени t на величину кратную
которую в результате тождественных преобразований можно привести к виду: Если дискретизации подлежит нормальный (гауссов) случайный процесс, энергетический спектр которого имеет прямоугольную форму, то коэффициенты Таким образом, непрерывные сообщения можно передавать в цифровом виде, то есть в виде последовательности чисел, при этом каждое число приближенно выражает величину соответствующего коэффициента
Билет 8. Билет 9. 1.Производительность марковского источника. Избыточность.
1. Производительность марковского источника. Избыточность. Согласно Марковской модели условная вероятность выбора источником очередной Xih буквы зависит только от
Если последнее равенство не зависит от времени, то есть справедливо при любом значении k, источник называется однородным. Однородный марковский источник называется стационарным, если безусловная вероятность выбора очередной буквы не зависит от k (p (xi,k)= p (xi)). Вычислив производительность источника для простой цепи Маркова ( В случае Марковской цепи Для производительности марковского источника всегда справедливо неравенство Hu Максимального значения, равного log mx, производительность источника достигает, когда отсутствует статистическая зависимость между буквами в слове и когда все буквы алфавита вырабатываются с равными вероятностями. Очевидно, максимальная производительность источника полностью определяется размером алфавита mх. Для того чтобы характеризовать, насколько полно использует источник возможности алфавита, вводится параметр Для передачи заданного количества информации, равного I, требуется n = I /H u букв. В случае, когда производительность источника достигает своего максимального значения, равного Отсюда I = n*Ни = nо * Нmах или Т.о., избыточность показывает, какая часть букв в слове не загружена информацией. Когда отношение
Одной из основных характеристик, используемых при проектировании информационных систем, является энтропия. Поэтому часто возникает необходимость определения закона распределения случайной величины X, при котором энтропия H(X) имеет максимальное значение. Для дискретного множества X было установлено, что при равномерном распределении вероятностей энтропия H(X) имеет максимальное значение, равное Экстремальные свойства относительной энтропии удобно интерпретировать через объем подпространства, который занимают типичные последовательности. Согласно равенству Приведем несколько примеров. 1. Пусть известно, что область X возможных значений случайной величины ограничена интервалом n - мерного куба, сторона которого равна
Приведенные рассуждения не являются строгим доказательством последнего равенства. Строгое доказательство можно найти в литературе. 2. Если на случайную величину X наложить следующие ограничения: а) область возможных значений неограничена б) известно среднее значение величины X; в) задана дисперсия 3. В случае, когда
Билет 10. Билет.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 , изображающую сообщение или сигнал, можно разложить в обобщенный ряд Фурье по полной системе ортонормированных функций:
, изображающую сообщение или сигнал, можно разложить в обобщенный ряд Фурье по полной системе ортонормированных функций: ,
, конечна [9].
конечна [9]. называется ортогональной на отрезке [ a, b ], если
называется ортогональной на отрезке [ a, b ], если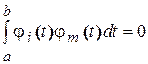 при
при 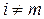 ,
, называется нормированной, если
называется нормированной, если .
. фиксированном числе членов ряда n значения коэффициентов
фиксированном числе членов ряда n значения коэффициентов  можно выбрать такими, при которых среднеквадратичная ошибка аппроксимации
можно выбрать такими, при которых среднеквадратичная ошибка аппроксимации
 .
. . Указанную последовательность можно интерпретировать как вектор в n - мерном Евклидовом пространстве с координатами
. Указанную последовательность можно интерпретировать как вектор в n - мерном Евклидовом пространстве с координатами 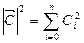 .
. .
.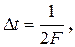 где F - верхняя граничная частота спектра сигнала. В этом случае функции
где F - верхняя граничная частота спектра сигнала. В этом случае функции ,
, , при этом каждая из них достигает своего максимального значения в те моменты времени, когда значения всех остальных функций равны нулю. Коэффициенты разложения определяются по формуле
, при этом каждая из них достигает своего максимального значения в те моменты времени, когда значения всех остальных функций равны нулю. Коэффициенты разложения определяются по формуле ,
, , то есть
, то есть 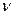 предшествующих. Математической моделью сообщений, вырабатываемых таким источником, являются цепи Маркова
предшествующих. Математической моделью сообщений, вырабатываемых таким источником, являются цепи Маркова 
 , имеем
, имеем 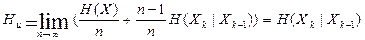 .
. .
. .
. , называемый избыточностью.
, называемый избыточностью. , для передачи того же количества информации I требуется минимальное количество букв, равное
, для передачи того же количества информации I требуется минимальное количество букв, равное  .
. . Учитывая последнее равенство, выражение для избыточности можно записать в виде
. Учитывая последнее равенство, выражение для избыточности можно записать в виде 
 или более приближенно
или более приближенно  .
. . Однако, в случае систем с непрерывным множеством состояний аналогичная задача не имеет решения, если на непрерывную случайную величину X априори не наложить некоторые ограничения.
. Однако, в случае систем с непрерывным множеством состояний аналогичная задача не имеет решения, если на непрерывную случайную величину X априори не наложить некоторые ограничения. , чем больше объем указанного пространства, тем больше относительная энтропия H(Х) (больше неопределенность того, какая из типичных последовательностей будет выбрана).
, чем больше объем указанного пространства, тем больше относительная энтропия H(Х) (больше неопределенность того, какая из типичных последовательностей будет выбрана). ,
,  . Найдем распределение, обладающее при этом максимальной относительной энтропией. Очевидно энтропия H(X) будет иметь максимальное значение, если подобласть определения типичных последовательностей будет совпадать с областью определения всех последовательностей. Только в этом случае объем
. Найдем распределение, обладающее при этом максимальной относительной энтропией. Очевидно энтропия H(X) будет иметь максимальное значение, если подобласть определения типичных последовательностей будет совпадать с областью определения всех последовательностей. Только в этом случае объем  имеет максимальное значение
имеет максимальное значение  , равное объему
, равное объему . При этом энтропия
. При этом энтропия .
.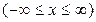 ;
; случайной величины
случайной величины  , то закон распределения, доставляющий максимум энтропии
, то закон распределения, доставляющий максимум энтропии  , будет нормальным.
, будет нормальным. может принимать только положительные значения
может принимать только положительные значения  при
при 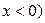 и первый момент
и первый момент  , максимальное значение энтропии
, максимальное значение энтропии  достигается при
достигается при .
.


