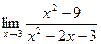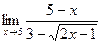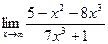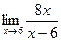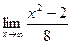Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность функции в точкеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Функция f(x), xÎ (a; b) называется непрерывной в точке xоÎ (a; b), если предел функции f(x) в точке хо существует и равен значению функции в этой точке:
Согласно данному определению, непрерывность функции f(x) в точке хо означает выполнимость следующих условий: 1) функция f(x) должна быть определена в точке хо; 2) у функции f(x) должен существовать предел в точке хо; 3) предел функции f(x) в точке хо должен совпадать со значением функции в этой точке.
Пример. Функция f(x) = x2 определена на всей числовой прямой и непрерывна в точке х = 1 поскольку f( 1 ) = 1 и
Непрерывность функции на множестве Определение. Функция f(x), называется непрерывной на интервале (a; b), если она непрерывна в каждой точке этого интервала. Если функция непрерывна в некоторой точке, то эта точка называется точкой непрерывности данной функции. В тех случаях, когда предел функции в данной точке не существует или его значение не совпадает со значением функции в данной точке, то функция называется разрывной в этой точке, а сама точка – точкой разрыва функции f(x). Свойства непрерывных функций. 1) Сумма конечного числа функций, непрерывных в точке а, есть функция, непрерывная в этой точке. 2) Произведение конечного числа функций, непрерывных в точке а, есть функция, непрерывная в этой точке. 3) Отношение конечного числа функций, непрерывных в точке а, есть функция, непрерывная в этой точке, если значение функции, стоящей в знаменателе, отлично от нуля в точке а. Пример. 1) Функция f(x) = xп, где n Î N, непрерывна на всей числовой прямой. Доказать этот факт можно, используя свойство 2 и непрерывность функции f(x) = x. 2) Функция f(x) = сxп (с – константа) непрерывна на всей числовой прямой, исходя из свойства 2 и примера 1. Теорема 2. Любая дробно-рациональная функция непрерывна в каждой точке своей области определения. Пример. 1) Функция 2)  непрерывна всюду на R, т.к. знаменатель нигде не обращается в нуль. непрерывна всюду на R, т.к. знаменатель нигде не обращается в нуль.
Определение Функция f(x) называется непрерывной в точке х = а, если в этой точке ее приращение
Односторонние пределы функции* Левосторонний предел функции. Если отыскивается предел функции f(x) при условии, что х, стремясь к а, может принимать только такие значения, которые меньше а, то этот предел, если он существует, называется левосторонним пределом функции f (х) (или левым пределом функции). Для того чтобы показать, что х стремится к а, оставаясь меньше а, употребляется запись: Правосторонний предел функции. Если отыскивается предел функции f(x) при условии, что х, стремясь к а, может принимать только такие значения, которые больше а, то этот предел, если он существует, называется правосторонним пределом функции f(x) (или правым пределом функции). То, что х, стремясь к а, остается больше а, обозначается так: Очевидно, что предел функции при Определение Функция f(x) называется непрерывной при х = а, если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, т. е. f(a). То есть:
Точки разрыва и их классификация* Если равенство Точка разрыва первого рода
Точка разрыва второго рода
Устранимый разрыв Определение. Если в точке х = а функция f(x) имеет левосторонний и правосторонний пределы и эти пределы между собой равны, но их значения не совпадают со значением функции в точке а, т. е. со значением f(a), то точка х = а называется точкой устранимого» разрыва. Таким образом, в этом случае Пример. Пользуясь определением непрерывности функции через предел Решение. Выразим приращение функции при произвольном приращении аргумента в некоторой точке х:
Подставим полученные выражения в формулу приращения функции, и после упрощения получим:
Найдем предел приращения функции при приращении аргумента, стремящемся к 0: 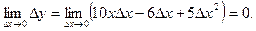
В итоге получаем, что при любом значении х предел приращения функции равен нулю, что доказывает ее непрерывность при любом значении х. Пример. Исследуем на непрерывность при х = 1 следующую функцию:
Решение. Так как знаменатель Если
так как при Теперь определим правосторонний предел функции. Если х →1 + 0, можно положить х = 1 + α (α > 0) и считать, что α, оставаясь положительной, стремится к нулю. Тогда, заменяя х на 1 + α, получим:
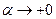 величина величина 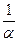 бесконечно большая, бесконечно большая, 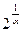 также бесконечно велика, также бесконечно велика, 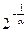 – величина бесконечно малая, т.е. ее предел будет равен 0. – величина бесконечно малая, т.е. ее предел будет равен 0.
Итак, у функции существуют и левосторонний предел, равный 2, и правосторонний предел, равный 3, но между собой они не равны. Из этого мы заключаем, что точка
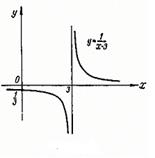
Пример. Построим графики и определим, какого рода разрыв имеет функция в данной точке (если точка не указана, определим точки разрыва самостоятельно): 1) Решение. 1) в точке 2) в точке 3) функция имеет точки разрыва
Вопросы для самоконтроля
Контрольные задания Вычислить пределы функции:
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 1009; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.233.69 (0.007 с.) |

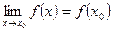 .
.
 непрерывна на всей числовой прямой, кроме точки
непрерывна на всей числовой прямой, кроме точки  , в которой знаменатель дроби обращается в нуль.
, в которой знаменатель дроби обращается в нуль. стремится к нулю, когда приращение аргумента
стремится к нулю, когда приращение аргумента  стремится к нулю, или иначе: функция f (х) называется непрерывной в точке х = а, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. если
стремится к нулю, или иначе: функция f (х) называется непрерывной в точке х = а, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. если 
 , а левосторонний предел функции обозначается символом:
, а левосторонний предел функции обозначается символом: 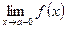 .
. , а правосторонний предел функции обозначается символом:
, а правосторонний предел функции обозначается символом:  .
. существует только тогда, когда существуют и равны между собой ее левосторонний и правосторонний пределы, т. е. когда
существует только тогда, когда существуют и равны между собой ее левосторонний и правосторонний пределы, т. е. когда 
 .
.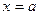 говорят, что она является точкой разрыва.
говорят, что она является точкой разрыва. Рис. 2
Рис. 2

 то точка а называется точкой разрыва первого рода (см. рис. 2).
то точка а называется точкой разрыва первого рода (см. рис. 2).
 а) б)
а) б)

 . Разрыв «устраняется» тем, что полагают
. Разрыв «устраняется» тем, что полагают  .
.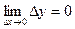 , докажем, что функция
, докажем, что функция 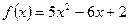 непрерывна в произвольной точке.
непрерывна в произвольной точке.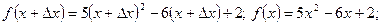
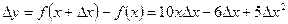 .
.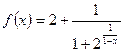 .
.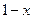 дроби равен нулю при
дроби равен нулю при 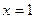 , то функция разрывна при
, то функция разрывна при 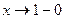 , то можно представить
, то можно представить 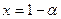 ,
, 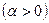 и считать, что
и считать, что 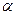 , оставаясь положительной, стремится к нулю. Заменяя х на
, оставаясь положительной, стремится к нулю. Заменяя х на 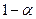 , получим:
, получим: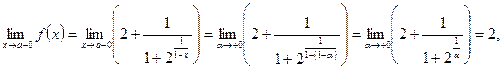
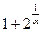 – бесконечно большая величина, обратная ей величина
– бесконечно большая величина, обратная ей величина 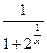 бесконечно мала:
бесконечно мала: 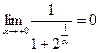 , а потому
, а потому 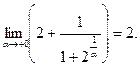
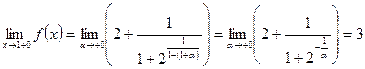 ,
,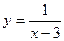 ,
, 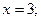 2)
2) 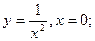 3)
3) 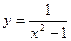 .
.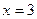 функция имеет разрыв второго рода, поскольку не имеет в этой точке ни одного конечного предела (см. рис. 5, а).
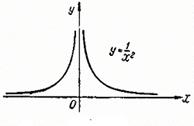
функция имеет разрыв второго рода, поскольку не имеет в этой точке ни одного конечного предела (см. рис. 5, а).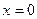 функция имеет разрыв второго рода, поскольку не имеет в этой точке ни одного конечного предела (см. рис. 5, в).
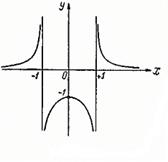
функция имеет разрыв второго рода, поскольку не имеет в этой точке ни одного конечного предела (см. рис. 5, в).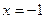 . В обеих точках функция имеет разрыв второго рода (см. рис. 5, б).
. В обеих точках функция имеет разрыв второго рода (см. рис. 5, б).